当前位置：网站首页>BinaryIndexedTrees树状数组

BinaryIndexedTrees树状数组

2022-08-03 18:26:00 【兴趣使然的小小】

引入：

针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：

数组不变，求区间和：「前缀和」、「树状数组」、「线段树」
多次修改某个数（单点），求区间和：「树状数组」、「线段树」
多次修改某个区间，输出最终结果：「差分」
多次修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间范围大小）

这样看来，「线段树」能解决的问题是最多的，那我们是不是无论什么情况都写「线段树」呢？

答案并不是，而且恰好相反，只有在我们遇到第 4 类问题，不得不写「线段树」的时候，我们才考虑线段树。

因为「线段树」代码很长，而且常数很大，实际表现不算很好。我们只有在不得不用的时候才考虑「线段树」。

总结一下，我们应该按这样的优先级进行考虑：

简单求区间和，用「前缀和」
多次将某个区间变成同一个数，用「线段树」
其他情况，用「树状数组」

原理：

树状数组

树状数组和线段树具有相似的功能，但他俩毕竟还有一些区别：
树状数组能有的操作，线段树一定有；
线段树有的操作，树状数组不一定有。
树状数组的代码要比线段树短，思维更清晰，速度也更快，在解决一些单点修改的问题时，树状数组是不二之选。
整体的时间复杂度O(nlog_2n) 空间复杂度O(n)

lowbit含义

先上一段代码,可以看到lowbit只有一行操作,而且是位运算,执行效率非常高

private int lowbit(int x) {
    
    return x & (-x);
}

忘记对饮含义的可以先看一下: [原码、反码、补码，计算机中负数的表示 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/47719434#:~:text= 补码：正数的补码就是其原码；负数的反码%2B1就是补码。如单字节的5的补码为：0000,0101；-5的原码为1111 1011。在计算机中，正数是直接用原码表示的，如单字节5，在计算机中就表示为：0000 0101。)

我们列出一下的表格:

x	1	2	3	4	5	6	7	8	9
lowbit(x)	1	2	1	4	1	2	1	8	1

注意: x不能等于0, 否则会进入死循环, 所以树状数组通常使用的下标会执行+1操作

区间求和

区间求和可以使用前缀和来计算,区间[l,r]的和为

sum(l,r)=preSum(r)−preSum(l−1)

所以区间求和,转换为求索引x的前缀和,
回到本题, int sumRange(int left, int right) 需要计算right的前缀和,left的前缀和,然后相减就是结果

定义树状数组

首先定义一个累加和数组 sums , 假设数组有8个元素,如图所示,其中ni是原始数据, si是累加和数据

为了求索引为7的前缀和可以快速通过累加和数组sums求得

preSum(7)=s(7) + s(6) + s(4)

更新/查询树状数组

更新树状数组时使用 x += lowBit(x)来寻找被影响的数组下标

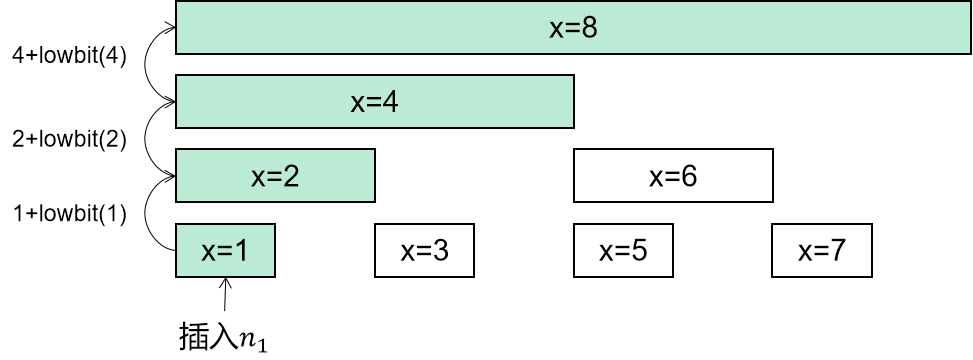
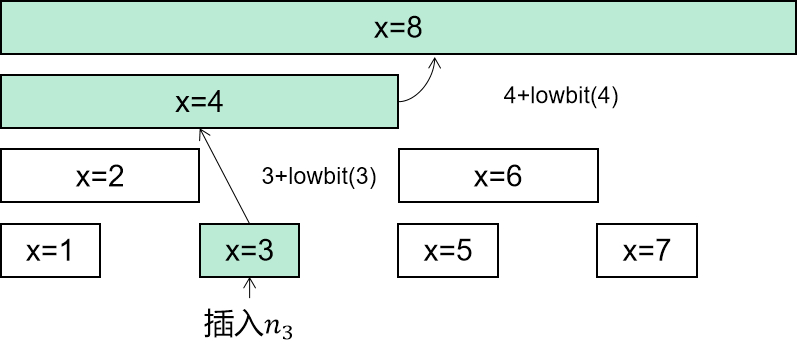
查询树状数组时使用 x -= lowBit(x) 来寻找小于x的下一个区间:

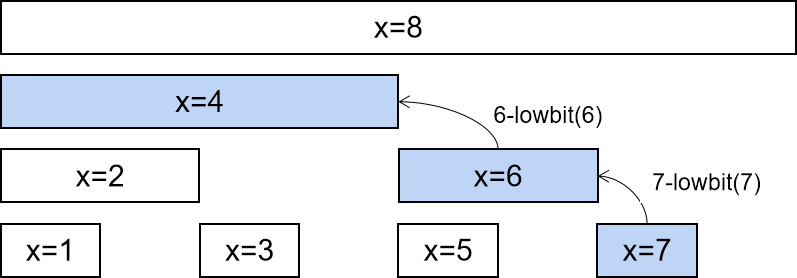
        /** * 查询树状数组 */
        public int query(int x) {
    
            int s = 0;
            while (x != 0) {
    
                s += sums[x];
                x -= lowBit(x);
            }
            return s;
        }
        /** * 插入数字,初始化 */
        private void insert(int index, int val) {
    
            // 下标+1
            int x = index + 1;
            while (x < sums.length) {
    
                sums[x] = sums[x] + val;
                x += lowBit(x);
            }
        }

模板：

        /*===================下面是模板==============================*/
        /** * 插入数字,初始化 */
        private void insert(int index, int val) {
    
            // 下标+1
            int x = index + 1;
            while (x < sums.length) {
    
                sums[x] = sums[x] + val;
                x += lowBit(x);
            }
        }
        /** * 查询树状数组 */
        public int query(int x) {
    
            int s = 0;
            while (x != 0) {
    
                s += sums[x];
                x -= lowBit(x);
            }
            return s;
        }

        /** * 计算lowBit */
        private int lowBit(int x) {
    
            return x & (-x);
        }

        /** * 更新数组以及累加和 */
        public void update(int index, int val) {
    
            int x = index + 1;
            while (x < sums.length) {
    
                // 减去之前nums[index]的值, 加上新的值
                sums[x] = sums[x] - nums[index] + val;
                x += lowBit(x);
            }
            nums[index] = val;
        }

        public int sumRange(int left, int right) {
    
            return query(right + 1) - query(left);
        }

题目实战：

区域和检索 - 数组可修改

307. 区域和检索 - 数组可修改 - 力扣（LeetCode）

本题显然属于第 2 类问题：多次修改某个数，求区间和。
我们使用「树状数组」进行求解。
「树状数组」本身是一个很简单的数据结构，但是要搞懂其为什么可以这样「查询」&「更新」还是比较困难的（特别是为什么可以这样更新），往往需要从「二进制分解」进行出发理解。
因此我这里直接提供「树状数组」的代码，大家可以直接当做模板背过即可。

    //树状数组
    class NumArray {
    
        //上来就写这三种方法.
        int[] tree;
        int lowbit(int x) {
    
            return x & -x;
        }
        int query(int x) {
    
            int ans = 0;
            for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
            return ans;
        }
        void add(int x, int u) {
    
            for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
        }

        int[] nums;
        int n;
        public NumArray(int[] _nums) {
    
            nums = _nums;
            n = nums.length;
            tree = new int[n + 1];
            for (int i = 0; i < n; i++) add(i + 1, nums[i]);
        }

        //然后修改
        public void update(int i, int val) {
    
            add(i + 1, val - nums[i]);
            nums[i] = val;
        }

        //求和
        public int sumRange(int l, int r) {
    
            return query(r + 1) - query(l);
        }
    }