数组与字符串8-最长回文子串

最长回文子串

题目：给你一个字符串 s，找到 s 中最长的回文子串。
二 题解
对于回文字符串，如下图所示，有两种情况：
第一种是以一个字符串为中心，该字符串两边对应位置的元素相等。第二种是以两个字符串为中心，字符串两边对应位置的元素相等。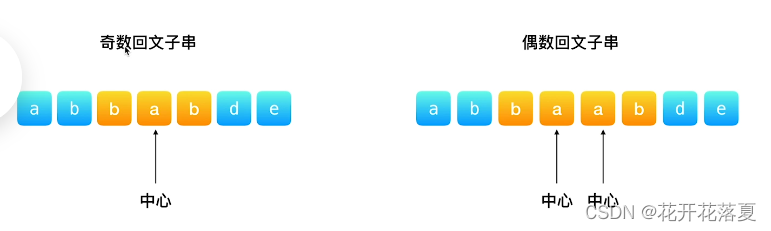
解题思路是：遍历字符串中的每一个字符，每遍历一个字符，就把该字符(index = i)作为中心，来求该字符的回文子字符串。由于子字符串有奇数回文子串和偶数回文子串两种情况，因此对于每个中心字符(index=i)，都求奇数回文子串和偶数回文子串两种情况。之后取两个子串中更长的那个，作为该中心字符串的回文子串。同时在遍历的过程中，使用i与max来记录拥有最长回文子串的中心字符的位置，和子串长度。

class Solution {
    
    public String longestPalindrome(String s) {
    
        if(s.length()<2){
    
            return s;
        }else{
    
            int begin = 0;
            int max = 0;
            for(int i=0;i<s.length()-1;i++){
    
                int oddMax = getPalindrome(s,i,i);
                int evenMax = getPalindrome(s,i,i+1);
                if(Math.max(oddMax,evenMax)>max){
    
                    begin = i;
                    max = Math.max(oddMax,evenMax);
                }
            }
            return s.substring(begin-(max-1)/2,begin+1+max/2);
        }   
    }

    private int getPalindrome(String s,int left,int right){
    
        while(left>=0&&right<s.length()&&s.charAt(left)==s.charAt(right)){
    
            left --;
            right ++;
        }
        return right-left-1;
    }   
}

三 动态规划解法
首先，对于一个字符串，例如：cacbcdf，求它的最长回文子串。我们可以先使用暴力搜索的想法来考虑：
对于c：
c
ca
cac
cacb
cacbc
cacbcd
cacbcdf
对于a:
a
ac
acb
acbc
acbcd
acbcdf
依次类推，在暴力搜索中，从cacbcd与acbc我们就可以看出，在重复的判断acbc是否为回文字符串。因此我们可以使用动态规划的思想来解题。对于一个字符串s的子串s[l][r]，是否为回文子串，取决于s[l]==s[r]且s[l+1][r-1]为回文子串。此时：r-1>l+1,即r>l+2时，s[l+1][r-1]才为一个字符串。我们可以根据下图构建动态规划的状态转移方程，对于left=0,right=5的子字符串，若s[l]==s[r]且s[1][4]为回文子串，则s[0][5]为回文子串。因此我们可以一列一列的填表，下一列进行s[l+1][r-1]是否为回文子串的判断时，总会用到前面已经计算出来的结果。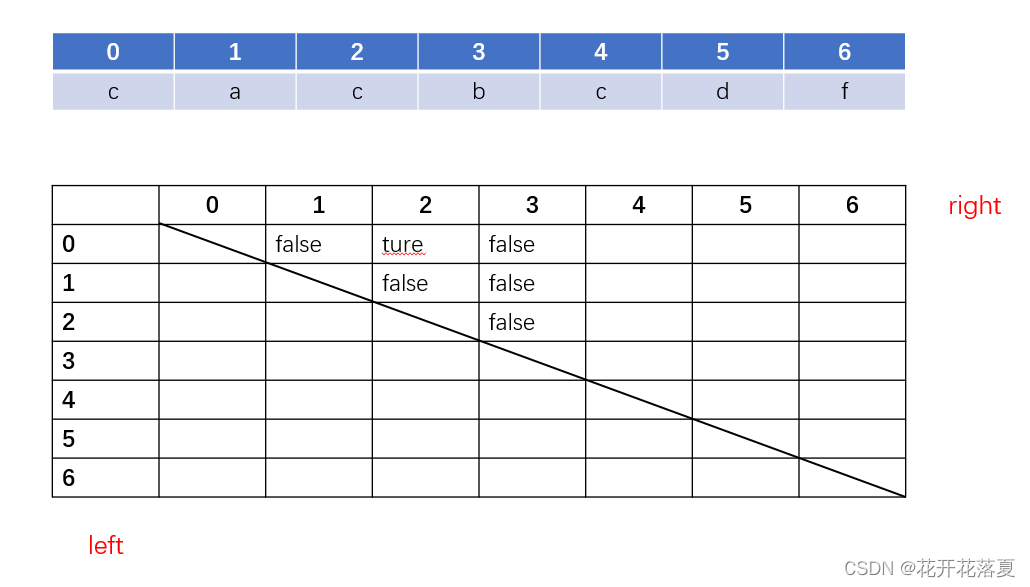
代码：

class Solution {
    
    public String longestPalindrome(String s) {
    
       if(s.length()<2){
    
            return s;
        }else{
    
            int left = 0;
            int right = 0;
            int Max = 1;
            Boolean[][] tmp = new Boolean[s.length()][s.length()];
            for(int i=0;i<s.length();i++){
    
                tmp[i][i]=true;
            }
            for(int r=1;r<s.length();r++){
    
                for(int l=0;l<r;l++){
    
                    if(s.charAt(l)==s.charAt(r)&&(r-l<=2 || tmp[l+1][r-1])){
    
                        tmp[l][r]=true;
                        if(r-l+1>Max){
    
                            Max = r-l+1;
                            left = l;
                            right = r;
                        }
                    }else{
    
                        tmp[l][r]=false;
                    }
                }
            }
            return s.substring(left,right+1);
        }
    }
}

动态规划效率不是很高呀