当前位置:网站首页>法向量点云旋转
法向量点云旋转
2022-07-04 09:32:00 【Coding的叶子】
在点云处理过程中,我们有时需要根据法向量把点云旋转到指定方向。例如,我们需要把激光雷达点云中地面旋转到与xoy平面平行。本节将详细介绍其中原理和python代码。
1 平面方程
平面方程可以用如下公式表示:
则(A, B, C)为平面的一个法向量,推导方式请参考博客:python三维点云投影(一)_Coding的叶子的博客-CSDN博客_点云投影。
2 法向量旋转
如下图所示,假设向量n0是原始法向量,n1是目标向量方向。我们的目标是将n0旋转到n1方向。n0的坐标为(x0, y0, z0),n1的坐标为(x1, y1, z1),原点坐标为O(0, 0, 0)。这三个坐标构成了一个平面,并且旋转轴垂直于该平面,且经过坐标原点,即该平面的法向量。通过这三个点计算出平面方程如下:

即:
则该平面的一个法向量为 ,也就是旋转轴的向量。
,也就是旋转轴的向量。
向量n0到向量n1的旋转角度theta为这两个向量之间的夹角,即:

3 open3d点云旋转
点云旋转的方法已在博客:点云旋转平移(三)—python open3d点云旋转_Coding的叶子的博客-CSDN博客_python 点云旋转详细介绍,包括欧拉角旋转、轴角旋转、四元数旋转等。这里采用轴角的方式进行旋转,其中旋转轴向量的模长为旋转角度大小。根据第2节中的旋转轴向量和旋转角度即可得到open3d中所需要的轴向量,计算公式如下:

4 参考代码
点云可视化的方式种类较多,如open3d、mayavi、pcl、matplotib、cloudcompare等,在之前的博客里都有介绍。这里采用matplotlib的方式进行点云可视化。如果还需要将点云进一步平移,可以参考本专栏之前的博客。
# -*- coding: utf-8 -*-
"""
乐乐感知学堂公众号
@author: https://blog.csdn.net/suiyingy
"""
import numpy as np
import open3d as o3d
import matplotlib.pyplot as plt
from copy import deepcopy
def viz_matplot(points):
x = points[:, 0] # x position of point
y = points[:, 1] # y position of point
z = points[:, 2] # z position of point
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, # x
y, # y
z, # z
c=z, # height data for color
cmap='rainbow',
marker=".")
ax.axis()
def pcd_rotate_normal(pointcloud, n0, n1):
"""
Parameters
----------
pointcloud : open3d PointCloud, 输入点云
n0 : array, 1x3, 原始法向量
n1 : array, 1x3, 目标法向量
Returns
-------
pcd : open3d PointCloud, 旋转后点云
"""
pcd = deepcopy(pointcloud)
n0_norm2 = np.sqrt(sum(n0 ** 2))
n1_norm2 = np.sqrt(sum(n1 ** 2))
theta = np.arccos(sum(n0 * n1) / n0_norm2 / n1_norm2)
r_axis = np.array([n1[2]*n0[1]-n0[2]*n1[1], n0[2]*n1[0]-n1[2]*n0[0], n0[0]*n1[1]-n1[0]*n0[1]])
r_axis = r_axis * theta / np.sqrt(sum(r_axis ** 2))
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(p)
R = pcd.get_rotation_matrix_from_axis_angle(r_axis.T)
pcd.rotate(R)
return pcd
if __name__ == '__main__':
#生成平面点云
x = np.arange(301).reshape(-1, 1).repeat(100, 0) / 100.
y = np.arange(301).reshape(-1, 1).repeat(100, 1).T.reshape(-1, 1) / 100.
#平面方程
z = (12 - 4*x -4*y) / 3
p = np.concatenate((x, y, z), 1)
p = p[np.where(p[:,2]>=0)]
viz_matplot(p)
#原始法向量
n0 = np.array([4, 4, 3])
#目标法向量
n1 = np.array([0, 0, 1])
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(p)
pcd = pcd_rotate_normal(pcd, n0, n1)
p = np.array(pcd.points)
#旋转后z的值应该基本相等
print('min Z: ', np.min(p[:, -1]), 'max Z: ', np.max(p[:, -1]))
viz_matplot(p)
plt.show()5 旋转效果
旋转前和旋转后的图片如下图所示。目标法向量为(0,0,1),即于xoy平面垂直,旋转后的平面应与xoy平面平行。
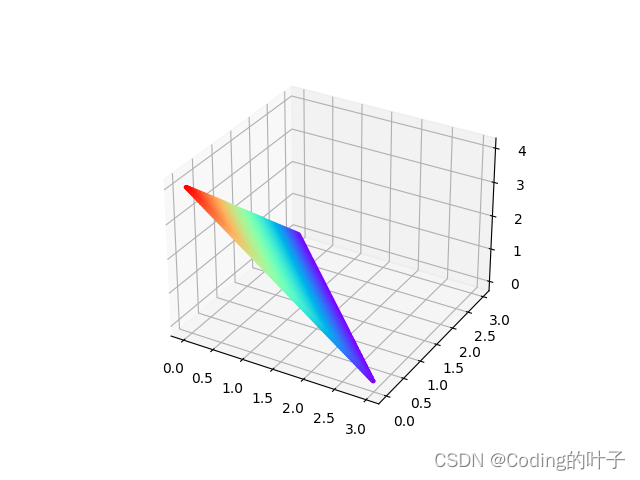
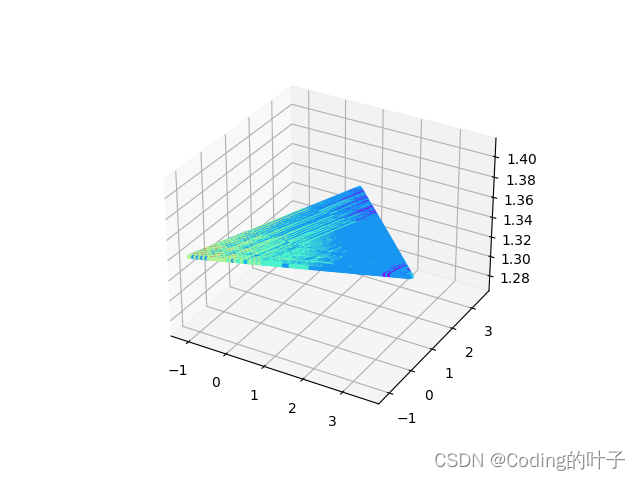
6 【python三维深度学习】python三维点云从基础到深度学习_Coding的叶子的博客-CSDN博客_python 三维点云
更多三维、二维感知算法和金融量化分析算法请关注“乐乐感知学堂”微信公众号,并将持续进行更新。
边栏推荐
- Global and Chinese markets of hemoglobin analyzers in care points 2022-2028: Research Report on technology, participants, trends, market size and share
- Investment analysis and prospect prediction report of global and Chinese high purity tin oxide Market Ⓞ 2022 ~ 2027
- Write a jison parser from scratch (5/10): a brief introduction to the working principle of jison parser syntax
- Multilingual Wikipedia website source code development part II
- After unplugging the network cable, does the original TCP connection still exist?
- Lauchpad x | MODE
- MySQL transaction mvcc principle
- 2022-2028 global industrial gasket plate heat exchanger industry research and trend analysis report
- Awk from entry to earth (14) awk output redirection
- Launpad | basic knowledge
猜你喜欢
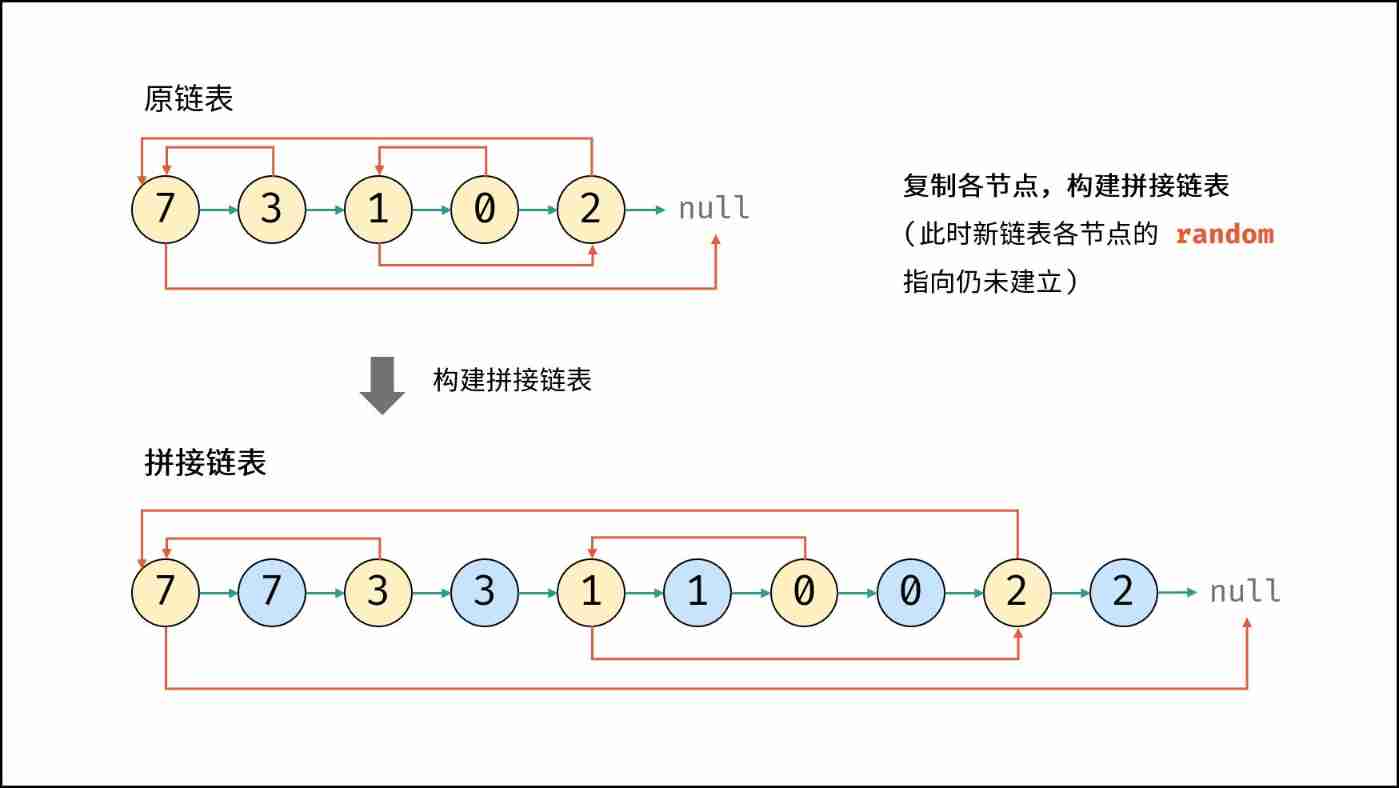
Leetcode (Sword finger offer) - 35 Replication of complex linked list

At the age of 30, I changed to Hongmeng with a high salary because I did these three things
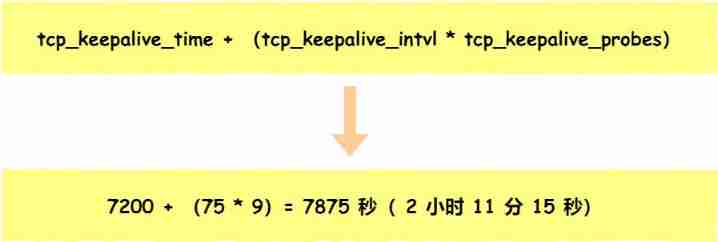
After unplugging the network cable, does the original TCP connection still exist?

2022-2028 global gasket metal plate heat exchanger industry research and trend analysis report
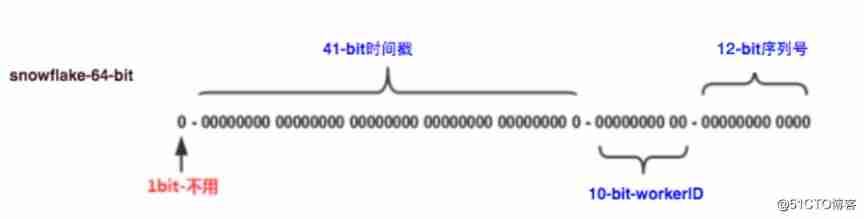
How to ensure the uniqueness of ID in distributed environment
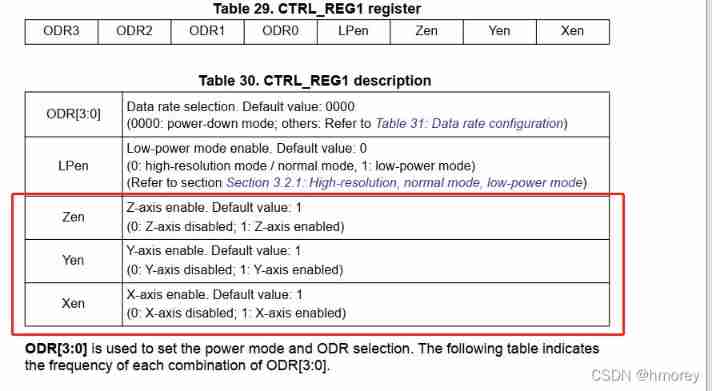
AMLOGIC gsensor debugging
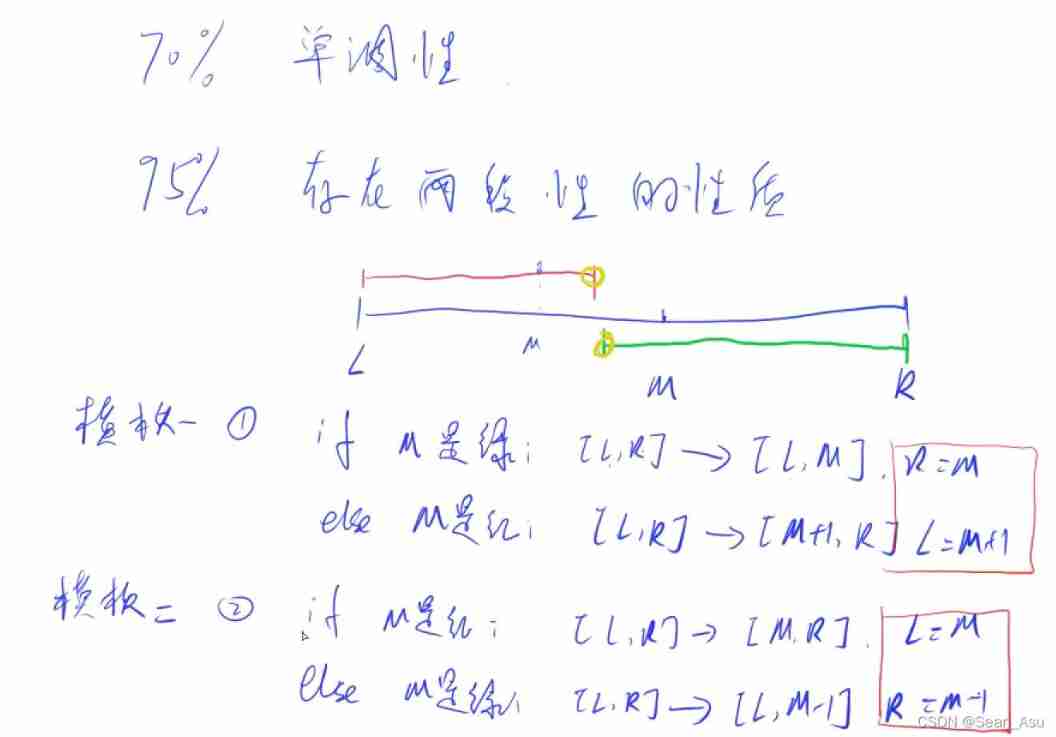
LeetCode 74. Search 2D matrix

Daughter love in lunch box
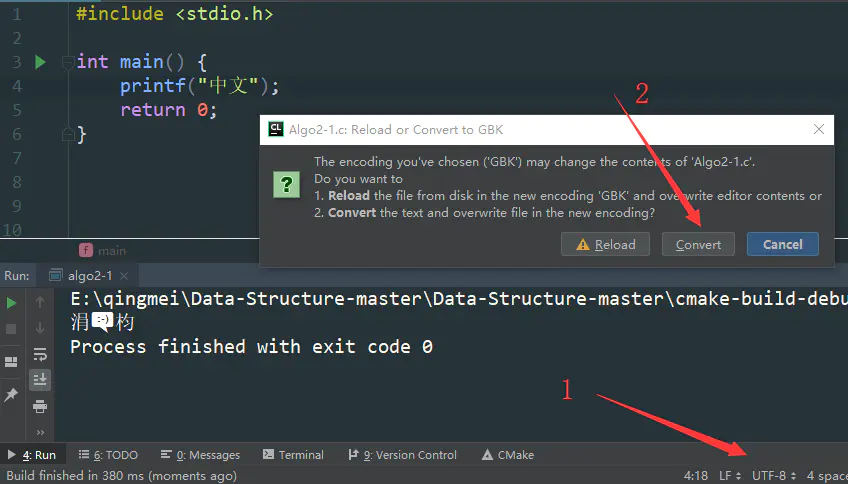
Clion console output Chinese garbled code

2022-2028 research and trend analysis report on the global edible essence industry
随机推荐
Launpad | basic knowledge
Global and Chinese markets for laser assisted liposuction (LAL) devices 2022-2028: Research Report on technology, participants, trends, market size and share
Deadlock in channel
2022-2028 global probiotics industry research and trend analysis report
Lauchpad x | MODE
Analysis report on the development status and investment planning of China's modular power supply industry Ⓠ 2022 ~ 2028
Leetcode (Sword finger offer) - 35 Replication of complex linked list
C语言-入门-基础-语法-[运算符,类型转换](六)
Research Report on research and investment prospects of China's testing machine industry (2022 Edition)
If you can quickly generate a dictionary from two lists
How should PMP learning ideas be realized?
Flutter tips: various fancy nesting of listview and pageview
Are there any principal guaranteed financial products in 2022?
Sword finger offer 30 contains the stack of Min function
LinkedList in the list set is stored in order
How do microservices aggregate API documents? This wave of show~
2022-2028 global gasket metal plate heat exchanger industry research and trend analysis report
Jianzhi offer 09 realizes queue with two stacks
Development trend and market demand analysis report of high purity tin chloride in the world and China Ⓔ 2022 ~ 2027
Some points needing attention in PMP learning