[untitled] forwarding least square method

Recently, a project of the company needs to be calculated TVDI（Temperature Vegetation Dryness Index , Temperature Vegetation Drought Index ） ,TVDI The calculation formula of is as follows （ The specific principle is self-contained ）：

among , Is the surface temperature of any pixel ; For a NDVI Corresponding minimum surface temperature , Corresponding to wet edge ; For a NDVI Corresponding maximum surface temperature , Corresponding to the dry side ;a,b Wet edged fitting Equation coefficient ,c,d Is the fitting equation coefficient of the dry edge .

In the process of fitting dry and wet edges , It is necessary to use the least square method to effectively NDVI and Lst Data for linear fitting . therefore , This paper is used in work C++ The least square fitting line realized , The key is to understand the basic principle of least square fitting line , It's easy to implement . The specific least square principle will not be elaborated too much , There are a lot of introduction materials on the Internet , Here we only give the shape as Linear regression calculation of a,b Coefficient and r^2 The final calculation formula of , The relevant code is as follows ：

[cpp]  view plain  copy

1. /************************************************************************* 
2.   The least square method is used to fit the straight line ,y = a*x + b; n Group data ; r- The correlation coefficient [-1,1],fabs(r)->1, explain x,y The linear relationship between them is good ,fabs(r)->0,x,y There is no linear relationship between , Fitting is meaningless  
3.  a = (n*C - B*D) / (n*A - B*B) 
4.  b = (A*D - B*C) / (n*A - B*B) 
5.  r = E / F 
6.   among ： 
7.  A = sum(Xi * Xi) 
8.  B = sum(Xi) 
9.  C = sum(Xi * Yi) 
10.  D = sum(Yi) 
11.  E = sum((Xi - Xmean)*(Yi - Ymean)) 
12.  F = sqrt(sum((Xi - Xmean)*(Xi - Xmean))) * sqrt(sum((Yi - Ymean)*(Yi - Ymean))) 
14. **************************************************************************/  
15. void LineFitLeastSquares(float *data_x, float *data_y, int data_n, vector<float> &vResult)  
16. {  
17.     float A = 0.0;  
18.     float B = 0.0;  
19.     float C = 0.0;  
20.     float D = 0.0;  
21.     float E = 0.0;  
22.     float F = 0.0;  
23.   
24.     for (int i=0; i<data_n; i++)  
25.     {  
26.         A += data_x[i] * data_x[i];  
27.         B += data_x[i];  
28.         C += data_x[i] * data_y[i];  
29.         D += data_y[i];  
30.     }  
31.   
32.     //  Calculate slope a And intercept b  
33.     float a, b, temp = 0;  
34.     if( temp = (data_n*A - B*B) )//  Judge whether the denominator is 0  
35.     {  
36.         a = (data_n*C - B*D) / temp;  
37.         b = (A*D - B*C) / temp;  
38.     }  
39.     else  
40.     {  
41.         a = 1;  
42.         b = 0;  
43.     }  
44.   
45.     //  Calculate the correlation coefficient r  
46.     float Xmean, Ymean;  
47.     Xmean = B / data_n;  
48.     Ymean = D / data_n;  
49.   
50.     float tempSumXX = 0.0, tempSumYY = 0.0;  
51.     for (int i=0; i<data_n; i++)  
52.     {  
53.         tempSumXX += (data_x[i] - Xmean) * (data_x[i] - Xmean);  
54.         tempSumYY += (data_y[i] - Ymean) * (data_y[i] - Ymean);  
55.         E += (data_x[i] - Xmean) * (data_y[i] - Ymean);  
56.     }  
57.     F = sqrt(tempSumXX) * sqrt(tempSumYY);  
58.   
59.     float r;  
60.     r = E / F;  
61.   
62.     vResult.push_back(a);  
63.     vResult.push_back(b);  
64.     vResult.push_back(r*r);  
65. }  

In order to verify the effectiveness of the algorithm , Give the following test data , The data source is the experimental data of a paper ：

[cpp]  view plain  copy

1. float pY[25] = { 10.98, 11.13, 12.51, 8.40, 9.27,  
2.                       8.73, 6.36, 8.50, 7.82, 9.14,  
3.                       8.24, 12.19, 11.88, 9.57, 10.94,  
4.                       9.58, 10.09, 8.11, 6.83, 8.88,  
5.                       7.68, 8.47, 8.86, 10.38, 11.08 };  
6.   
7. float pX[25] = { 35.3, 29.7, 30.8, 58.8, 61.4,  
8.                       71.3, 74.4, 76.6, 70.7, 57.5,  
9.                       46.4, 28.9, 28.1, 39.1, 46.8,  
10.                       48.5, 59.3, 70.0, 70.0, 74.5,  
11.                       72.1, 58.1, 44.6, 33.4, 28.6 };  

The data is in Excel The fitting result of is , among .

Reprinted address   http://blog.csdn.net/pl20140910/article/details/51926886

In engineering practice , We often encounter similar problems :

We did n Experiments , Got a set of data

then , We want to know x and y The functional relationship between . So we describe it in XOY In rectangular coordinates , Get the following point cloud ：

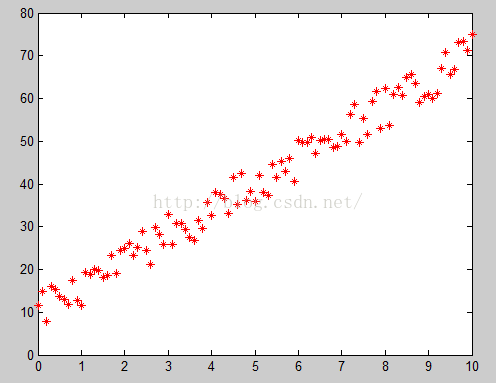
then , We found that ,x and y「 Probably 」 It's a linear relationship , Because we can roughly connect all the sample points with a straight line , Here's the picture ：

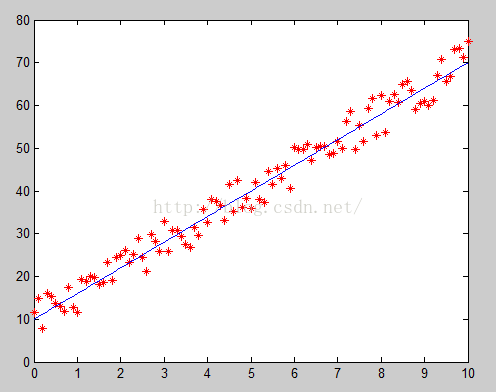
therefore , We can 「 guess 」. The next question , Is to find out a and b Value .

This seems to be a very simple problem ,a and b Are two unknowns , We just need to find two sample points randomly , List the equations ：

Two unknowns , Two equations , I can solve for that a and b Value .

However , It's wrong here , Or inaccurate . Why? ？ because    This functional relationship , It is our 「 guess 」 Of , It is not necessarily objective and correct （ Although it may be right ）. So we can't solve such a simple and rough set of equations .

Then what shall I do? ？ Since it is 「 guess 」 Of , Then there is an error . Then we will slightly revise this functional relationship to ：

here ,   They are the first i The dependent variable of the experiment 、 The independent variables 、 error .

Since it is 「 guess 」, Then of course we hope to guess more accurately . How to measure accurately ？ Nature and e It matters .

After the above formula is modified, you can get ：

ad locum ,a and b Is the independent variable ,e Is the function value .

This is the easiest place to get confused , Why? a,b It's an independent variable , instead of x,y？

This is to mention 「 Curve fitting 」 The concept of . So-called 「 fitting 」 That is, we need to find a function , Come on 「 matching 」 The sample value we obtained in the experiment . Put it in the example above , We need to adjust a and b Value , To make this function and the data obtained in the experiment more 「 matching 」. therefore ,a and b It's just 「 Curve fitting 」 Arguments in the process .

Next , Continue the problem of how to make the error smaller .

「 Least square method 」 The ideological core of , Is to define a loss function ：

obviously , If we adjust a and b, bring Q To achieve the minimum , that 「 Curve fitting 」 The error will also be minimal .

here ,Q yes a,b Function of . According to higher mathematics, only ,Q The minimum point of its derivative must be 0 The point of .

therefore , We make ：

After solving the above equations, we get about a,b A system of binary quadratic equations , Therefore, we can solve a and b Value . This is the whole process of the least square method .

The last show ：

（1） English name of least square method Least Squares, Actually translated into 「 The least square method 」, It's easier to understand . Its core is to define the loss function ;

（2） There is more than one method to evaluate errors , And things like    etc. （ Of course, this is not the least square method ）;

（3） The least square method can not only be used for fitting primary functions , It can also be used for fitting higher-order functions ;

（4） The least square method is both a method of curve fitting , It can also be used for optimization .