当前位置:网站首页>Ehrlich sieve + Euler sieve + interval sieve
Ehrlich sieve + Euler sieve + interval sieve
2022-07-04 08:38:00 【ccsu_ yuyuzi】
Ethmoid O(nloglogn)
The meaning of Ehrlich sieve is very simple , Every time I enumerate the prime numbers I have traversed now , Enumerate all its multiples in the interval , These enumerated numbers are composite numbers , When we enumerate the multiples of all primes in the interval , Mark them all , What is not marked is prime . This also ensures that the next enumeration must be prime , Because the composite number has been marked .
void getp()
{
int cnt=0;
vis[1]=1;
for(int i=2;i<=n;i++)// enumeration
if(vis[i]==0)// Judge whether it is a prime
for(int j=2;j*i<=n;j++)// Enumerating multiples
vis[i*j]=1;
return ;
}
/*
vis Marked as 1 Is not a prime number , Note that after the expansion of the Ehrlich sieve is the interval sieve
*/But there is a disadvantage of the sieve , We enumerate prime multiples every time , Will produce repeated enumeration , For example, a number is a multiple of some primes , The enumeration will be repeated several times . If we can eliminate duplicate enumeration , Under this premise , Created the Euler sieve .
Euler screen O(N)
The meaning of Euler sieve is optimized Ehrlich sieve . Every time we judge whether a number is prime , Then enumerate , But its European code is that each number will be enumerated only once . When the current number is divided by the prime factor of the traversal , We need to pay attention to , This number has been enumerated , direct break that will do .
void getp()
{
int cnt=0;
for(int i=2;i<=n;i++)
{
if(vis[i]==0)
p[++cnt]=i;
for(int j=1;j<=cnt&&p[j]*i<=n;j++)
{
vis[i*p[j]]=1;
if(i%p[j]==0)
break;
}
}
return ;
}Interval sieve The time complexity is similar to that of the sieve
Interval sieve is a variant of Ehrlich sieve , It is for a certain value , But the algorithm for solving the prime number problem in the interval whose length is still within the calculation range . We first have to enumerate 2 To  The prime number of . Then use these prime numbers to enumerate in the interval [L,R] Multiple of , The multiples of these enumerations are composite numbers , Mark directly , What is not marked in the interval is prime .
The prime number of . Then use these prime numbers to enumerate in the interval [L,R] Multiple of , The multiples of these enumerations are composite numbers , Mark directly , What is not marked in the interval is prime .
void segment_sieve(int a,int b)
{
for(int i=0;i<1e6+5;i++)
isprime[i]=lowisprime[i]=true;
for(int i=2;i*i<b;i++)
{
if(lowisprime[i])
{
for(int j=2*i;j*j<b;j+=i)
lowisprime[j]=false;
for(long long j=(a/i)*i;j<b;j+=i)
if(j>=a&&j<b)
isprime[j-a]=false;
}
}
}边栏推荐
- Codeforces Round #793 (Div. 2)(A-D)
- Unity write word
- @Role of pathvariable annotation
- Laravel page load problem connection reset - PHP
- 团体程序设计天梯赛-练习集 L1-006 连续因子
- [go basics] 1 - go go
- Turn: excellent managers focus not on mistakes, but on advantages
- Question 49: how to quickly determine the impact of IO latency on MySQL performance
- Cancel ctrl+alt+delete when starting up
- How to re enable local connection when the network of laptop is disabled
猜你喜欢

Codeforces Global Round 21(A-E)
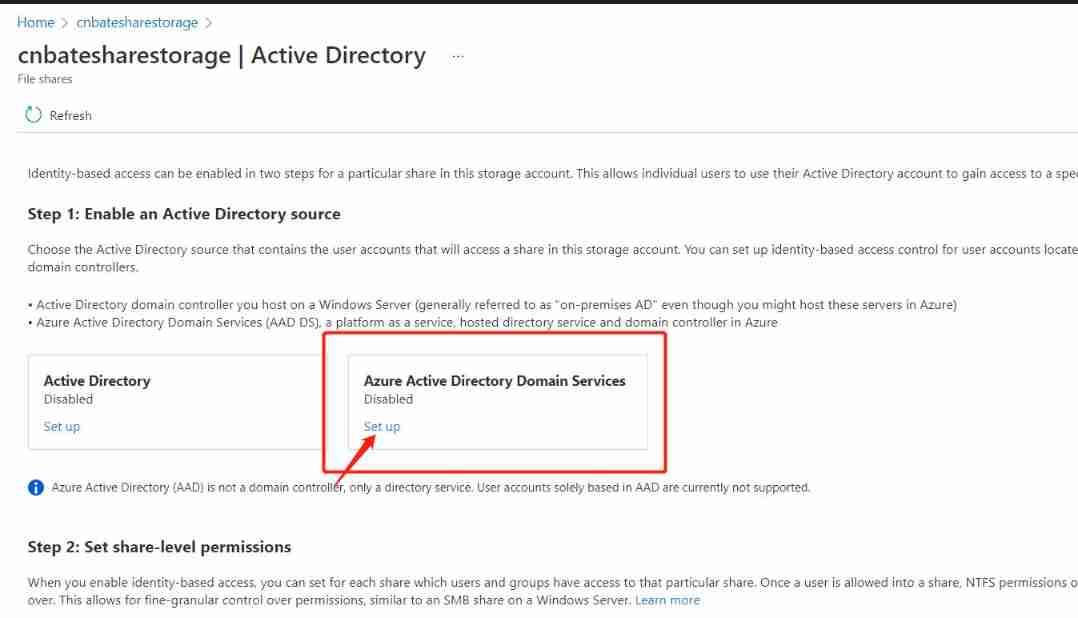
Azure ad domain service (II) configure azure file share disk sharing for machines in the domain service
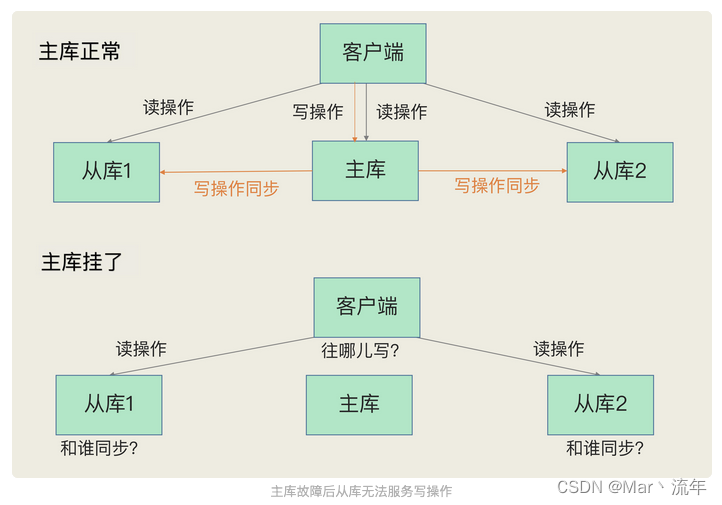
Redis sentinel mechanism
![Sports [running 01] a programmer's half horse challenge: preparation before running + adjustment during running + recovery after running (experience sharing)](/img/c8/39c394ca66348044834eb54c68c2a7.png)
Sports [running 01] a programmer's half horse challenge: preparation before running + adjustment during running + recovery after running (experience sharing)
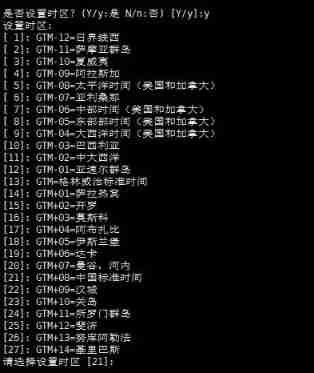
DM8 command line installation and database creation

Conversion of yolov5 XML dataset to VOC dataset
![[test de performance] lire jmeter](/img/c9/25a0df681c7ecb4a0a737259c882b3.png)
[test de performance] lire jmeter

Snipaste convenient screenshot software, which can be copied on the screen

es6总结
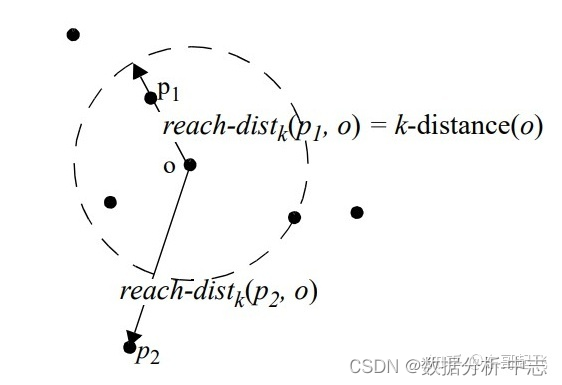
A method for detecting outliers of data
随机推荐
DM8 command line installation and database creation
C#,数值计算(Numerical Recipes in C#),线性代数方程的求解,Gauss-Jordan消去法,源代码
Sort by item from the list within the list - C #
Convert datetime string to datetime - C in the original time zone
Comprendre la méthode de détection des valeurs aberrantes des données
2022 examination questions for safety managers of metal and nonmetal mines (underground mines) and examination papers for safety managers of metal and nonmetal mines (underground mines)
Group programming ladder race - exercise set l2-002 linked list de duplication
根据数字显示中文汉字
[performance test] read JMeter
Educational Codeforces Round 119 (Rated for Div. 2)
C # implements a queue in which everything can be sorted
Leetcode 23. Merge K ascending linked lists
【无标题】转发最小二乘法
What if the wireless network connection of the laptop is unavailable
Four essential material websites for we media people to help you easily create popular models
Call Baidu map to display the current position
How to set multiple selecteditems on a list box- c#
1. Qt入门
广和通高性能4G/5G无线模组解决方案全面推动高效、低碳智能电网
NewH3C——ACL