【无标题】转发最小二乘法

最近公司的一个项目需要计算TVDI（Temperature Vegetation Dryness Index ，温度植被干旱指数） ，TVDI的计算公式如下（具体原理自行百度）：

其中，为任意像元的地表温度；为某一NDVI对应的最小地表温度，对应的是湿边；为某一NDVI对应的最大地表温度，对应的是干边；a，b为湿边的拟合方程系数，c，d为干边的拟合方程系数。

在拟合干边和湿边的过程中，需要利用最小二乘方法来对有效的NDVI和Lst数据来进行线性拟合。因此，本文记录在工作中用C++实现的最小二乘拟合直线，关键是理解最小二乘拟合直线的基本原理，实现起来比较简单。具体的最小二乘原理再此不做过多的阐述，网上有大量的介绍资料，这里只给出形如的线性回归计算a，b系数以及r^2的最终计算公式，相关代码如下：

[cpp]  view plain  copy

1. /************************************************************************* 
2.  最小二乘法拟合直线，y = a*x + b; n组数据; r-相关系数[-1,1],fabs(r)->1,说明x,y之间线性关系好，fabs(r)->0，x,y之间无线性关系，拟合无意义 
3.  a = (n*C - B*D) / (n*A - B*B) 
4.  b = (A*D - B*C) / (n*A - B*B) 
5.  r = E / F 
6.  其中： 
7.  A = sum(Xi * Xi) 
8.  B = sum(Xi) 
9.  C = sum(Xi * Yi) 
10.  D = sum(Yi) 
11.  E = sum((Xi - Xmean)*(Yi - Ymean)) 
12.  F = sqrt(sum((Xi - Xmean)*(Xi - Xmean))) * sqrt(sum((Yi - Ymean)*(Yi - Ymean))) 
14. **************************************************************************/  
15. void LineFitLeastSquares(float *data_x, float *data_y, int data_n, vector<float> &vResult)  
16. {  
17.     float A = 0.0;  
18.     float B = 0.0;  
19.     float C = 0.0;  
20.     float D = 0.0;  
21.     float E = 0.0;  
22.     float F = 0.0;  
23.   
24.     for (int i=0; i<data_n; i++)  
25.     {  
26.         A += data_x[i] * data_x[i];  
27.         B += data_x[i];  
28.         C += data_x[i] * data_y[i];  
29.         D += data_y[i];  
30.     }  
31.   
32.     // 计算斜率a和截距b  
33.     float a, b, temp = 0;  
34.     if( temp = (data_n*A - B*B) )// 判断分母不为0  
35.     {  
36.         a = (data_n*C - B*D) / temp;  
37.         b = (A*D - B*C) / temp;  
38.     }  
39.     else  
40.     {  
41.         a = 1;  
42.         b = 0;  
43.     }  
44.   
45.     // 计算相关系数r  
46.     float Xmean, Ymean;  
47.     Xmean = B / data_n;  
48.     Ymean = D / data_n;  
49.   
50.     float tempSumXX = 0.0, tempSumYY = 0.0;  
51.     for (int i=0; i<data_n; i++)  
52.     {  
53.         tempSumXX += (data_x[i] - Xmean) * (data_x[i] - Xmean);  
54.         tempSumYY += (data_y[i] - Ymean) * (data_y[i] - Ymean);  
55.         E += (data_x[i] - Xmean) * (data_y[i] - Ymean);  
56.     }  
57.     F = sqrt(tempSumXX) * sqrt(tempSumYY);  
58.   
59.     float r;  
60.     r = E / F;  
61.   
62.     vResult.push_back(a);  
63.     vResult.push_back(b);  
64.     vResult.push_back(r*r);  
65. }  

为了验证该算法的有效性，给出如下测试数据，数据来源为某论文的实验数据：

[cpp]  view plain  copy

1. float pY[25] = { 10.98, 11.13, 12.51, 8.40, 9.27,  
2.                       8.73, 6.36, 8.50, 7.82, 9.14,  
3.                       8.24, 12.19, 11.88, 9.57, 10.94,  
4.                       9.58, 10.09, 8.11, 6.83, 8.88,  
5.                       7.68, 8.47, 8.86, 10.38, 11.08 };  
6.   
7. float pX[25] = { 35.3, 29.7, 30.8, 58.8, 61.4,  
8.                       71.3, 74.4, 76.6, 70.7, 57.5,  
9.                       46.4, 28.9, 28.1, 39.1, 46.8,  
10.                       48.5, 59.3, 70.0, 70.0, 74.5,  
11.                       72.1, 58.1, 44.6, 33.4, 28.6 };  

该数据在Excel的拟合结果为，其中。

转载地址   http://blog.csdn.net/pl20140910/article/details/51926886

在工程实践中，经常遇到类似的问题:

我们做了n次实验，获得了一组数据

然后，我们希望知道x和y之间的函数关系。所以我们将其描绘在XOY直角坐标系下，得到下面这么一张点云图：

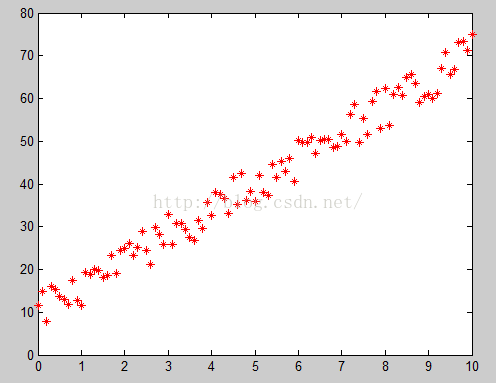
然后，我们发现，x和y「可能」是线性的关系，因为我们可以用一条直线大致的将所有的样本点串连起来，如下图：

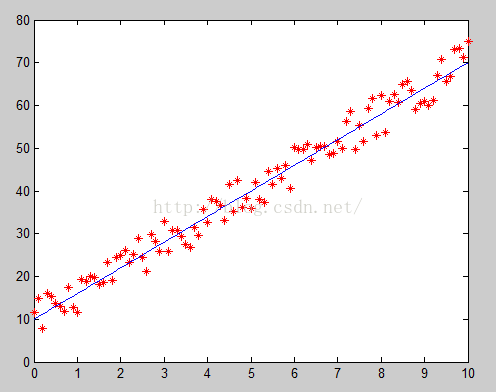
所以，我们可以「猜测」。接下来的问题，就是求出a和b的值。

这看起来是一个很简单的问题，a和b是两个未知数，我们只需要随意找出两个样本点，列出方程组：

两个未知数，两个方程，就可以求解出a和b的值。

然而，在这里是不对的，或者说是不准确的。为什么呢？因为  这个函数关系，是我们「猜测」的，并不一定是客观正确的（虽然也许是正确的）。所以我们不能这么简单粗暴的方程组求解。

那怎么办呢？既然是「猜测」的，那么就存在误差。那么我们将这个函数关系稍加修正为：

这里，  分别是第i次实验的因变量、自变量、误差。

既然是「猜测」，那我们当然希望猜得准一点。那怎么衡量准确呢？自然和e有关系。

上式变型后可得：

在这里，a和b才是自变量，e是函数值。

这里是最容易搞糊涂的地方，为什么a,b是自变量，而不是x,y？

这就要提及「曲线拟合」的概念。所谓「拟合」就是说我们要找到一个函数，来「匹配」我们在实验中获得的样本值。放到上面的例子，就是我们要调整a和b的值，来使得这个函数和实验中获得的数据更加「匹配」。所以，a和b才是「曲线拟合」过程中的自变量。

接下来，继续如何让误差更小的问题。

「最小二乘法」的思想核心，就是定义一个损失函数：

显然，如果我们调整a和b，使得Q达到最小，那么「曲线拟合」的误差也会最小。

这里，Q是a,b的函数。根据高等数学的只是，Q的最小值点必然是其导数为0的点。

所以，我们令：

求解上述方程组以后得到关于a,b的一个二元二次方程组，因此可以解得a和b的值。这就是最小二乘法的整个过程。

最后说明：

（1）最小二乘法英文名Least Squares，其实翻译成「最小平方法」，更容易让人理解。其核心就是定义了损失函数；

（2）评价误差的方法不止一个，还有诸如  等（当然这就不是最小二乘法了）；

（3）最小二乘法不仅可以用于一次函数的拟合，还可以用于更高次函数的拟合；

（4）最小二乘法既是一种曲线拟合的方法，也可用于最优化。