[CV] Wu Enda machine learning course notes | Chapter 9

If there is no special explanation in this series of articles , The text explains the picture above the text
machine learning | Coursera
Wu Enda machine learning series _bilibili

9 neural network ：Learning

9-1 Cost function applied to neural network

• use $L$ Represents the total number of layers of the neural network （Layers）
• use $s_l$ It means the first one $l$ Layer unit （ Neuron ） The number of （ The bias unit is not included ）
• $h_{\Theta }(x)\in {\mathbb{R}}^K$（$h_{\Theta }(x)$ by $K$ Dimension vector , Common to the output layer of neural network $K$ Neurons , That is to say $K$ Outputs ）
• $(h_{\Theta }(x){)}_i=i^{th}output$（$(h_{\Theta }(x){)}_i$ It means the first one $i$ Outputs ）

The cost function applied to neural networks is ：

$$J(\Theta )=-\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}^{(i)}log(h_{\Theta }(x^{(i)}){)}_k+(1-y_k^{(i)})log(1-(h_{\Theta }(x^{(i)}){)}_k)\right]+\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}({\Theta }_{ji}^{(l)}{)}^2$$

• In the second item ${\sum }_{i=1}^{s_l}{\sum }_{j=1}^{s_{l+1}}$ It means to be $s_{l+1}$ That's ok $s_l$ Columns of the matrix ${\Theta }_{ji}^{(l)}$ Add up each element in
• In the second item ${\sum }_{l=1}^{L-1}$ It refers to summing the matrices of the input layer and the hidden layer

9-2 Back propagation algorithm

• ${\delta }_j^{(l)}$ It is defined as the first $l$ Layer $j$ Deviation of neurons （“error”）
  
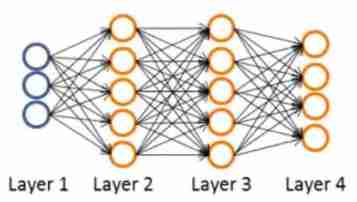
  Take the four layer neural network in the above figure as an example
• ${\delta }_j^{(4)}=a_j^{(4)}-y_j$（$y_j$ Refers to the first $j$ Output values in the data set ,$a_j^{(4)}$ It refers to the second of neural network $j$ Outputs ,$a_j^{(4)}$ It can also be expressed as $(h_{\Theta }(x){)}_j$）
• The above formula can be expressed as ${\delta }^{(4)}=a^{(4)}-y$, It can also be expressed as ${\delta }^{(4)}=h_{\Theta }(x)-y$
• ${\delta }^{(3)}=({\Theta }^{(3)}{)}^T{\delta }^{(4)}\cdot g^{\prime }(z^{(3)})$
  among $g^{\prime }(z^{(3)})=a^{(3)}\cdot (1-a^{(3)})$
• ${\delta }^{(2)}=({\Theta }^{(2)}{)}^T{\delta }^{(3)}\cdot g^{\prime }(z^{(2)})$
  among $g^{\prime }(z^{(2)})=a^{(2)}\cdot (1-a^{(2)})$

The result of dot multiplication is a number , The cross product is a vector

• $\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=a_j^{(l)}{\delta }_i^{(l+1)}$
  The regularization term is ignored here , The idea that $\lambda =0$
  
• The above figure is the flow of the back propagation algorithm , Finally, we can get $\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{ij}^{(l)}$, Then carry out gradient descent algorithm

9-3 Understand back propagation

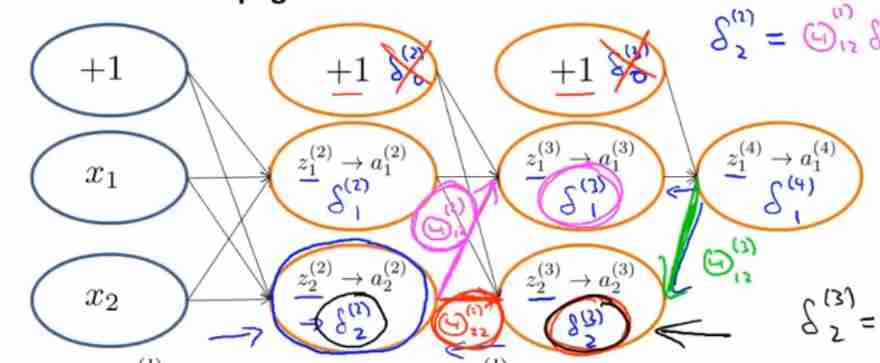
Take the neural network in the figure above as an example

• ${\delta }_2^{(2)}={\Theta }_{12}^{(2)}{\delta }_1^{(3)}+{\Theta }_{22}^{(2)}{\delta }_2^{(3)}$
• ${\delta }_2^{(3)}={\Theta }_{12}^{(3)}{\delta }_1^{(4)}$

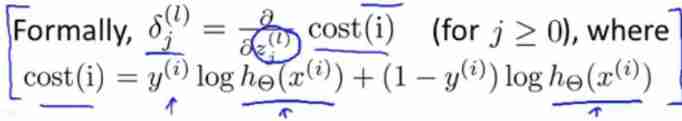
9-4 Expand parameters

9-5 Gradient detection

To estimate the cost function $J(\Theta )$ Upper point $(\theta ,J(\Theta ))$ Derivative at , Can use $\frac{\mathrm{d}}{\mathrm{d}\theta }J(\theta )\approx \frac{J(\theta +\epsilon )-J(\theta -\epsilon )}{2\epsilon }(\epsilon =10^{-4}byshould)$ Obtain derivative

Expand into vectors , Pictured above

• $\theta$ It's a $n$ Dimension vector , It's a matrix ${\Theta }^{(1)},{\Theta }^{(2)},{\Theta }^{(3)},...$ Expansion of
• It can be estimated that $\frac{\partial }{\partial {\theta }_n}J(\theta )$ Value

Compare the estimated partial derivative value with the partial derivative value obtained by back propagation , If the two values are very close , You can verify that the calculation is correct
Once it is determined that the value calculated by the back propagation algorithm is correct , You should turn off the gradient test algorithm

9-6 Random initialization

If at the beginning of the program $\Theta$ All elements in are 0, It will cause multiple neurons to calculate the same characteristics , Leading to redundancy , This becomes a symmetric weight problem
So when initializing, make ${\Theta }_{ij}^{(l)}$ be equal to $[-ϵ,ϵ]$ A random value in

9-7 Review summary

Train a neural network ：
1. Random an initial weight
2. Execute forward propagation algorithm , Get to all $x^{(i)}$ Of $h_{\Theta }(x^{(i)})$
3. Computational cost function $J(\Theta )$
4. Execute back propagation algorithm , Calculation $\frac{\partial }{\partial {\Theta }_{jk}^{(l)}}J(\Theta )$
(get $a^{(l)}$ and ${\delta }^{(l)}$ for $l=2,...,L$)
5. Estimated by gradient test algorithm $J(\Theta )$ Partial derivative of , Compare the estimated partial derivative value with the partial derivative value obtained by back propagation , If the two values are very close , It can be verified that the calculation result of the back propagation algorithm is correct ; After verification , Turn off the run Inspection Algorithm (disable gradient checking code)
6. Use gradient descent algorithm or other more advanced optimization methods , Combined with the back propagation calculation results , Get to make $J(\Theta )$ The smallest parameter $\Theta$ Value