Semantic segmentation ｜ learning record (4) expansion convolution (void convolution)

---

Preface

This blog mainly introduces the knowledge of dilation convolution , Expansion convolution （Dilated convolution） Also called void convolution （Atrous convolution）. When I first came into contact with this word, I really see deeplabv3+ I came across this word when I was writing my thesis , Here is a detailed introduction .

One 、 Expansion convolution

The following figure shows ordinary convolution ：k=3,r=1,p=0,s=1

The following figure shows expansion convolution ：k=3,r=2,p=0,s=1
We can find that these two convolutions are also used 3*3 Of kernel, But in expansion convolution ,kernel There is a gap , We call it Expansion factor r.

What's the use of expanding convolution ？

• Increase the receptive field
• Keep the original input characteristic graph W,H（ Pictured above , In actual use, it will padding Set to 1 In this way, we can ensure that the size of the feature map remains unchanged ）

Why use dilation convolution ？

In image classification network, we usually need to carry out multiple down sampling , Compare the following sampling 32 times , After that, the size of the original image will be restored by upsampling , But too much down sampling has a great impact on our restoration to the original image . take VGG16 Take the Internet as an example , stay VGG16 Through the Internet maxpooling Operate to down sample the picture to reduce the length and width , But doing so will lose some details and particularly small goals . And it cannot be restored through up sampling .
Someone will say , Then we will maxpooling Can you remove the layer ？ Get rid of maxpooling Layer is not a good method , This will reduce the receptive field .
So expansion convolution solves this problem , It can increase the receptive field , It can also ensure that the height and width of the input and output characteristic graph will not change .

Two 、gridding effect

Understanding Convolution for Semantic Segmentation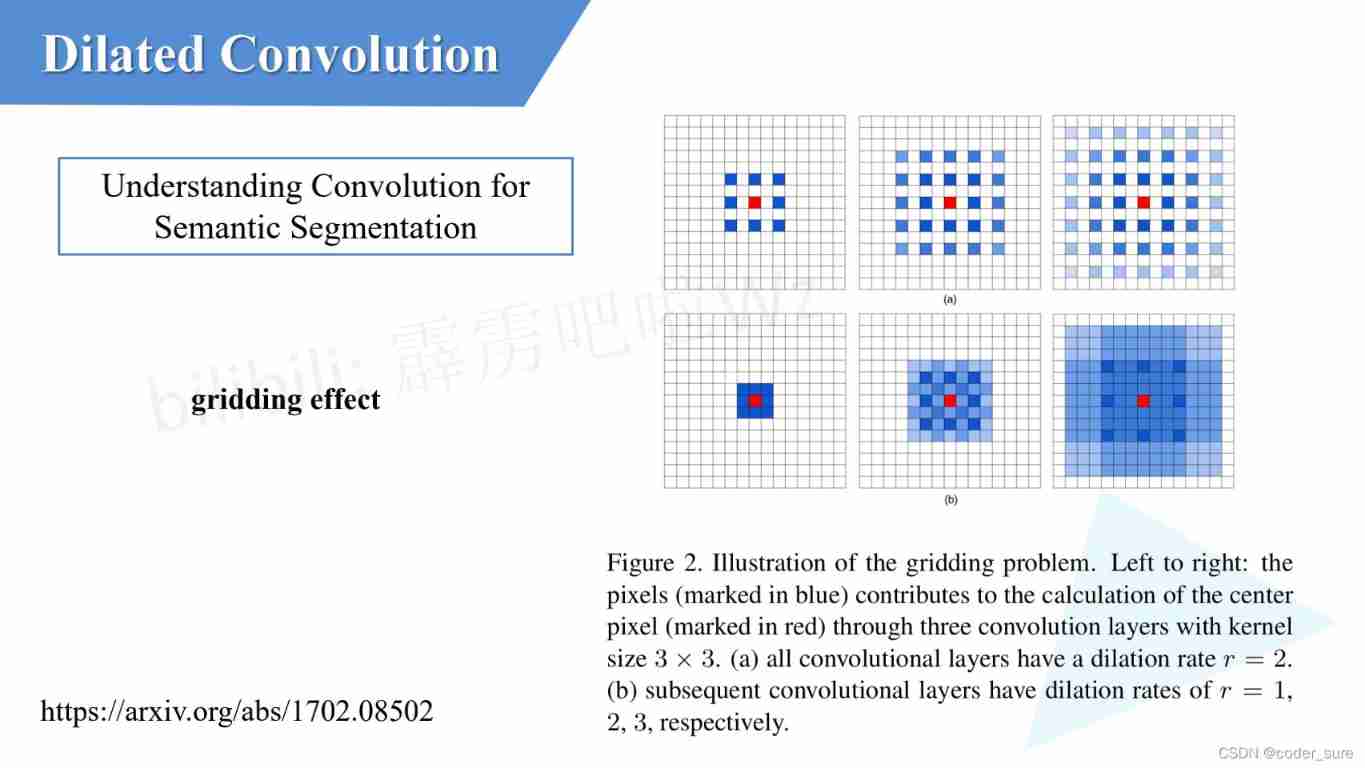

There are four convolutions in the figure below ：layer1 To Layer4 the 3 The operational convolution kernel of sub expansion convolution is $3\ast 3$, The coefficient of expansion is r2

Let's take a detailed look layer2 We used Layer1 What data is on ？
We see layer2 The previous pixel will be used as shown in the following figure 9 individual layer1 Parameters in position

Look again. layer3 We used Layer1 What data is on ？
We see layer3 The previous pixel will be used as shown in the following figure 25 individual layer1 Parameters in position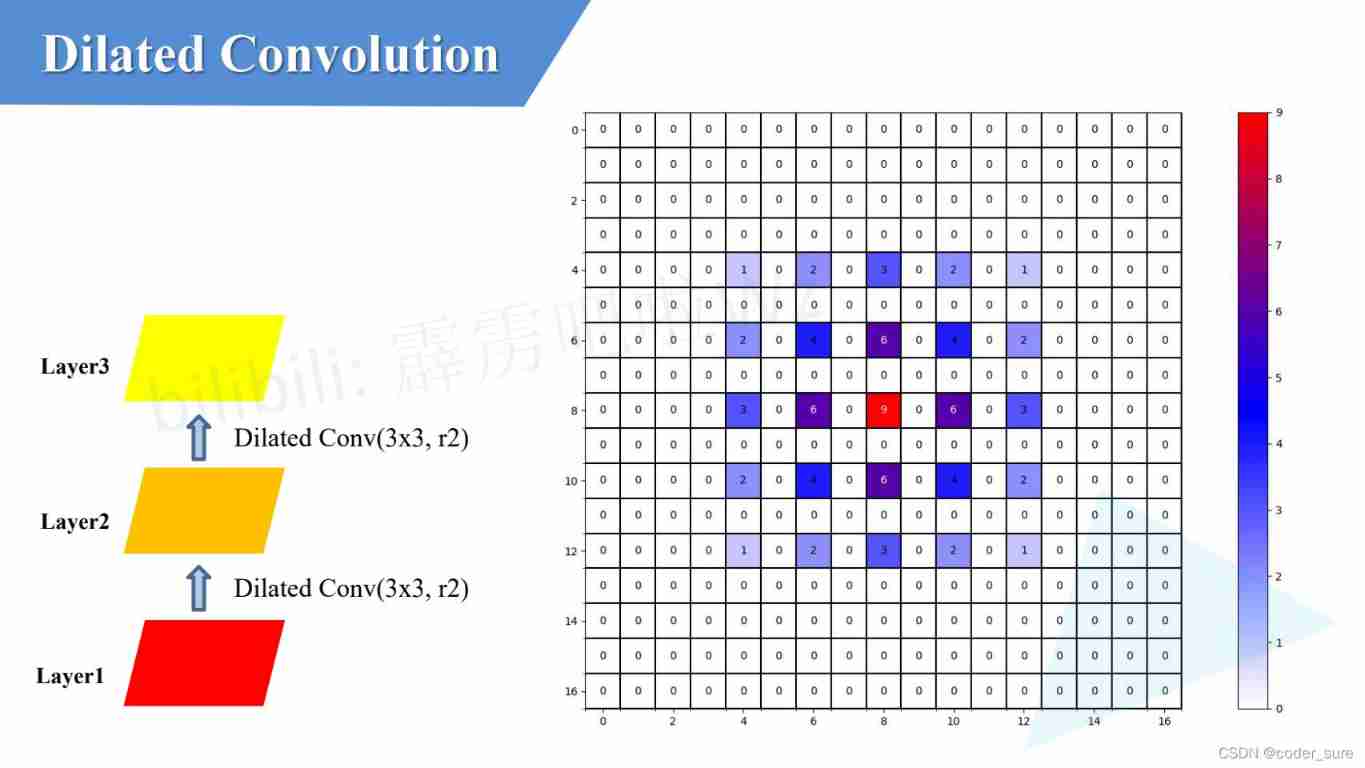

Look again. layer4 We used Layer1 What data is on ？
We see layer4 The previous pixel will be used as shown in the following figure 49 individual layer1 Parameters in position

At this time, we can observe , The underlying image pixels we use through dilation convolution are not continuous , There is a gap between every non-zero element , This will inevitably lead to the loss of feature information , This is gridding effect problem , We should also try to avoid gridding effect problem .

If we design the expansion factor of the cubic expansion convolution operation in the above figure r1,r2,r3 In the form of ：




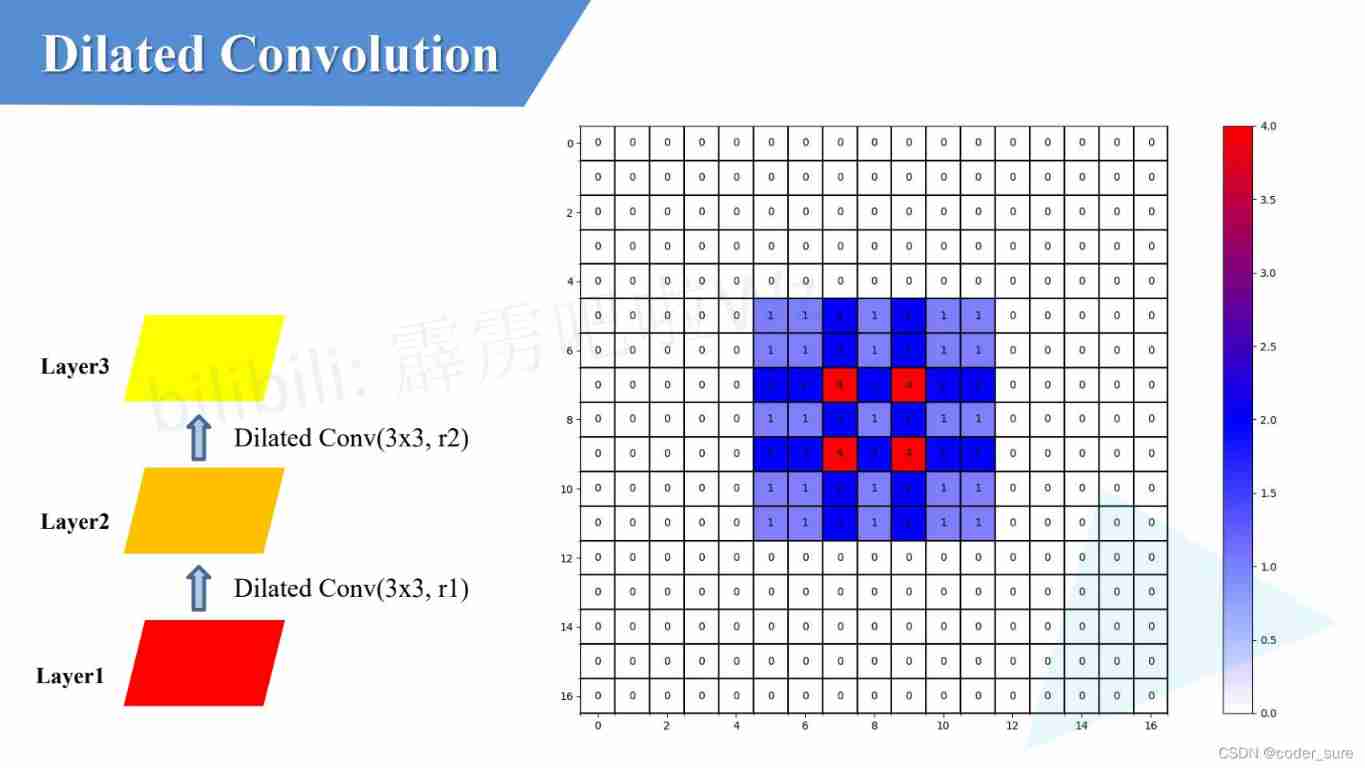
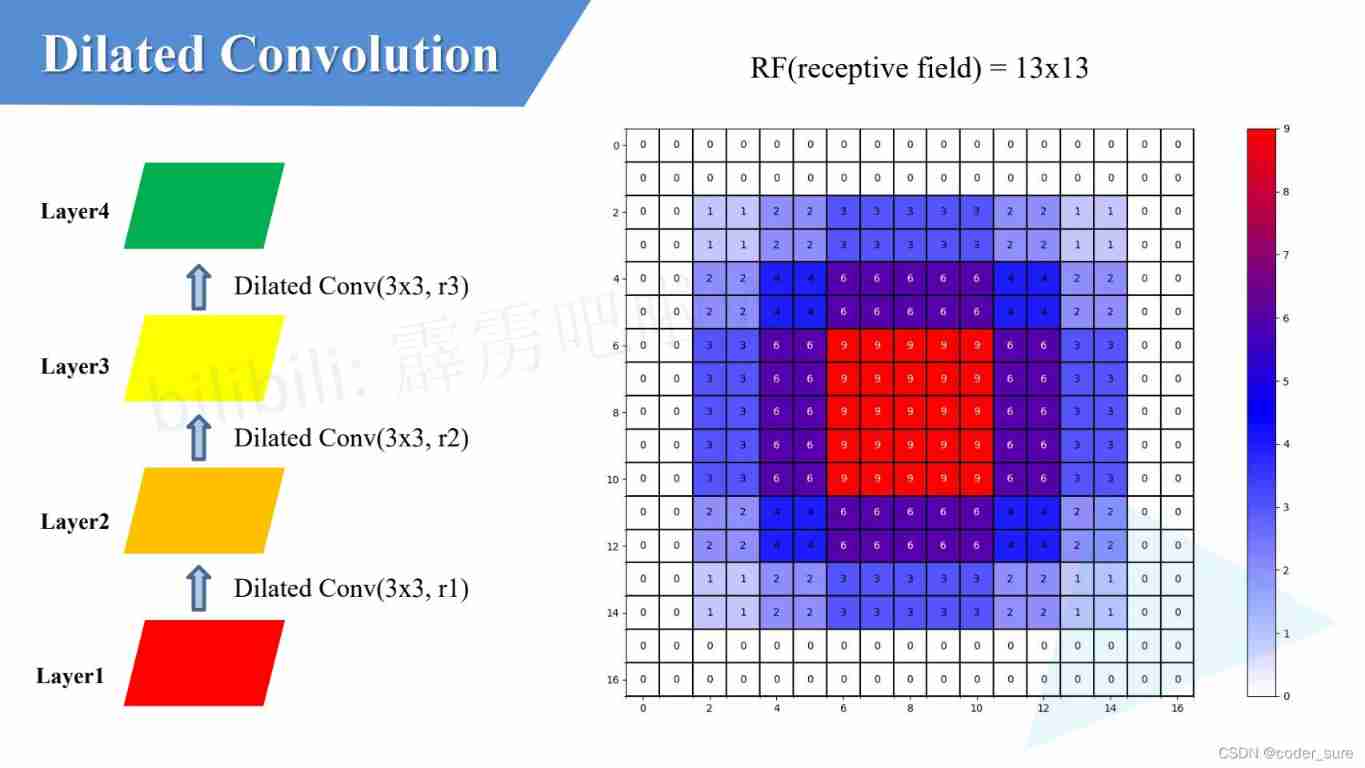
After setting the expansion coefficient in this way , The underlying information we use is continuous ！
Let's look at a group of experiments , If you use ordinary convolution ：




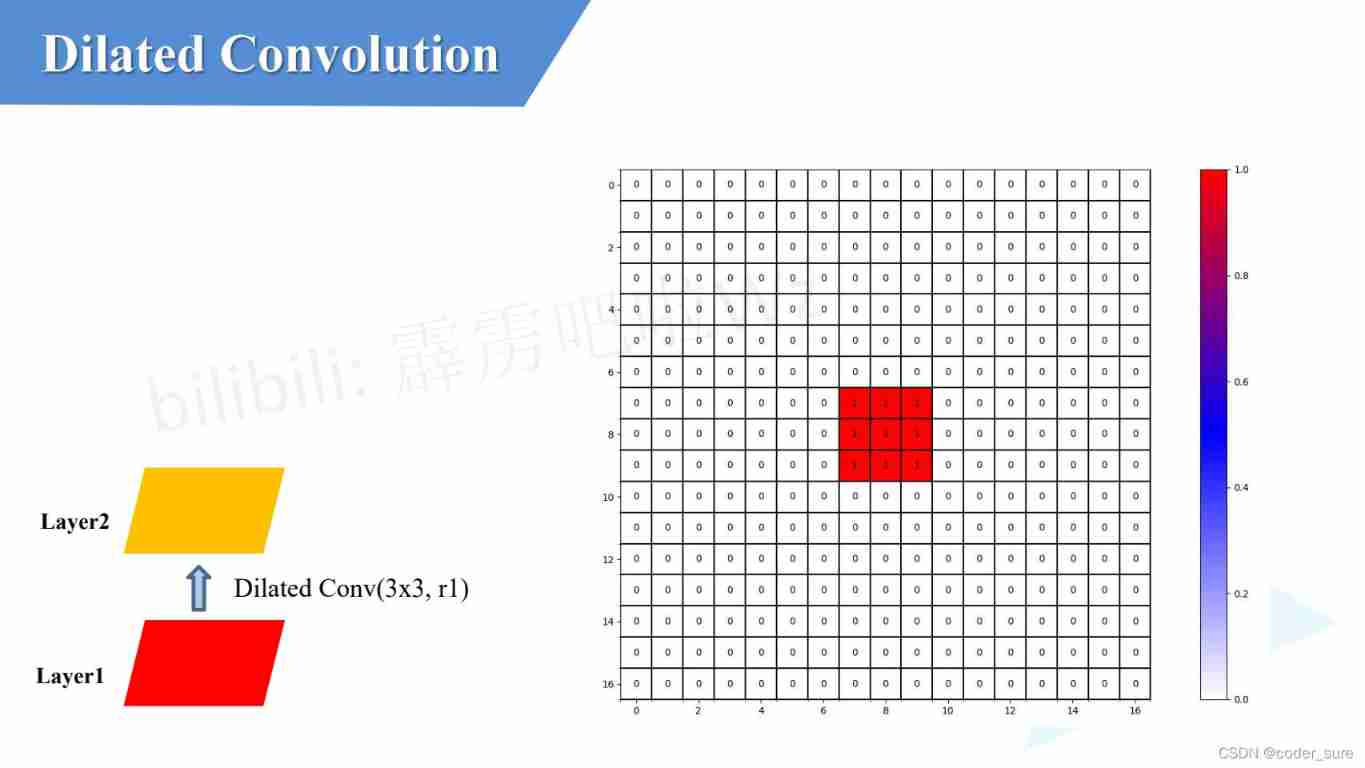
Obviously, we can see that under the same parameters, the receptive field of ordinary convolution is smaller than that of dilated convolution .

3、 ... and 、 When using multiple expansion convolutions , How to set the expansion coefficient ？

Understanding Convolution for Semantic Segmentation The method is given in this paper .
We can see in the experiment just now , The expansion coefficients used are 1,2,3 The effect of continuous convolution is better than that of convolution with the same expansion coefficient . So how to design the coefficient ？ The author puts forward HDC Design criteria ：

Let's use the actual code to test these two groups of examples of setting the expansion convolution coefficient in the paper ：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


def dilated_conv_one_pixel(center: (int, int),
                           feature_map: np.ndarray,
                           k: int = 3,
                           r: int = 1,
                           v: int = 1):
    """  The center of the expanded convolution kernel is in the specified coordinate center Location time , Count which pixels are used ,  And an increment is added at the utilized pixel position v Args: center:  The coordinates of the center of the expanded convolution kernel  feature_map:  A characteristic diagram that records the number of times each pixel is used  k:  Expansion convolution kernel kernel size  r:  Dilated convoluted dilation rate v:  Use times increment  """
    assert divmod(3, 2)[1] == 1

    # left-top: (x, y)
    left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
    for i in range(k):
        for j in range(k):
            feature_map[left_top[1] + i * r][left_top[0] + j * r] += v


def dilated_conv_all_map(dilated_map: np.ndarray,
                         k: int = 3,
                         r: int = 1):
    """  According to which pixels in the output characteristic matrix are used and how many times they are used ,  With expansion convolution k and r Calculate which pixels of the input characteristic matrix are used and how many times they are used  Args: dilated_map:  Record the characteristic diagram of the number of times each pixel is used in the output characteristic matrix  k:  Expansion convolution kernel kernel size  r:  Dilated convoluted dilation rate """
    new_map = np.zeros_like(dilated_map)
    for i in range(dilated_map.shape[0]):
        for j in range(dilated_map.shape[1]):
            if dilated_map[i][j] > 0:
                dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])

    return new_map


def plot_map(matrix: np.ndarray):
    plt.figure()

    c_list = ['white', 'blue', 'red']
    new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
    plt.imshow(matrix, cmap=new_cmp)

    ax = plt.gca()
    ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
    ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)

    #  Show color bar
    plt.colorbar()

    #  Mark the quantity in the drawing 
    thresh = 5
    for x in range(matrix.shape[1]):
        for y in range(matrix.shape[0]):
            #  Notice the matrix[y, x] No matrix[x, y]
            info = int(matrix[y, x])
            ax.text(x, y, info,
                    verticalalignment='center',
                    horizontalalignment='center',
                    color="white" if info > thresh else "black")
    ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
    plt.show()
    plt.close()


def main():
    # bottom to top
    dilated_rates = [1, 2, 3]
    # init feature map
    size = 31
    m = np.zeros(shape=(size, size), dtype=np.int32)
    center = size // 2
    m[center][center] = 1
    # print(m)
    # plot_map(m)

    for index, dilated_r in enumerate(dilated_rates[::-1]):
        new_map = dilated_conv_all_map(m, r=dilated_r)
        m = new_map
    print(m)
    plot_map(m)


if __name__ == '__main__':
    main()

r=[1,2,3]:

r=[1,2,5]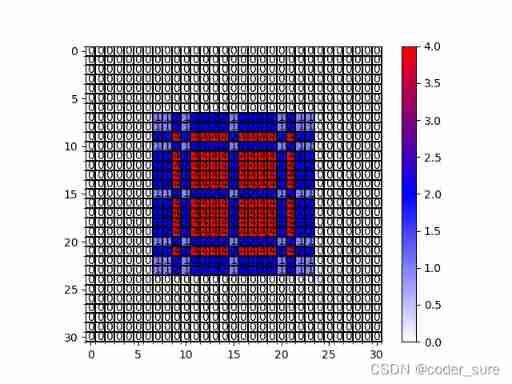

r=[1,2,9]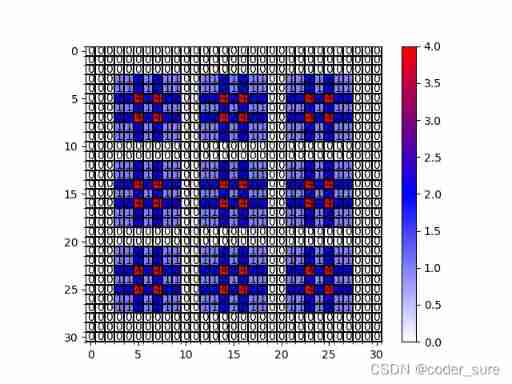

Four 、 Suggestions for setting expansion coefficient

• The suggestion is to dilation rates Set to sawtooth structure , for example [1,2,3,1,2,3]
• The common divisor of the expansion coefficient is not greater than 1
  for example r=[2,4,8]: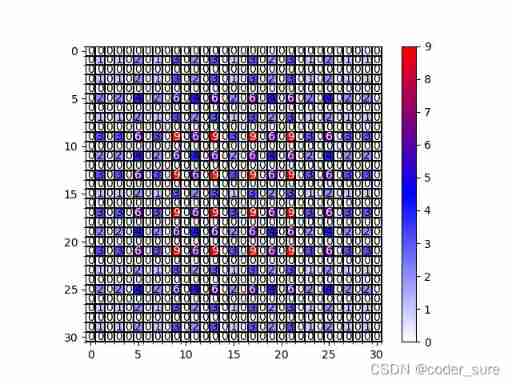
  
  If the expansion coefficient is set in this way , The feature map we get is not zero pixels nor continuous .

5、 ... and 、 Whether it is applied HDC Comparison of segmentation effects of design criteria

The first line is GT, The second line is ResNet-DUC model, The third line is application HDC Design criteria , It is obvious that the scientific setting of expansion coefficient has a positive impact on the segmentation effect .

6、 ... and 、 summary

• Introduced what is expansion convolution
• The role of expansion convolution
• Why use expansion convolution
• Determination method and influence of expansion convolution expansion coefficient

Reference material

up Lord thunderbolt Wz Original video
Source code of the program
Understanding Convolution for Semantic Segmentation