当前位置:网站首页>信息学奥赛一本通(1258:【例9.2】数字金字塔)
信息学奥赛一本通(1258:【例9.2】数字金字塔)
2022-08-02 20:02:00 【橙子教师】
1258:【例9.2】数字金字塔
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 20019 通过数: 11518
【题目描述】
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
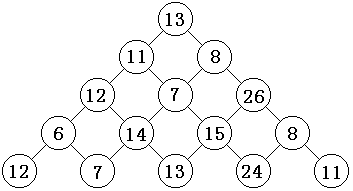
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
【输入】
第一个行包含R(1≤R≤1000),表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
【输出】
单独的一行,包含那个可能得到的最大的和。
【输入样例】
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11【输出样例】
86【分析】
方法1:顺推
设a[i][j]存储数塔,f[i][j]则记录从起点到第 i 层第 j 列的路径数字和。
(1)划分阶段。
阶段:每一层就是一个阶段;样例中共有五个阶段。
(2)确定状态和状态变量。
状态:二维数组中的每个值就是状态。状态信息用f[i][j]表示。
(2)确定决策并写出状态转移方程。
f[i][j]的值从哪来?当然是从上面第 i-1 行的第 j 列和第 j-1 列来。决策:来自上? 或是 来自左上?,策略:最大化路径。故:
状态转移方程:![f[i][j]=a[i][j]+max\left\{\begin{matrix} f[i-1][j-1]\\ f[i-1][j] \end{matrix}\right.](http://img.inotgo.com/imagesLocal/202208/02/202208022000269923_3.gif)
(4)寻找边界条件。
顺推时, 边界:f[1][1]=a[1][1]。目标:max(f[n][j])
(5)设计并实现程序。

【参考代码1】
#include <stdio.h>
#define MAXN 1010
int a[MAXN][MAXN]; //存储数塔数据
int f[MAXN][MAXN]; //f[i][j]表示从起点到i层j列的路径数字和
int max(int x,int y)
{
return x > y ? x : y;
}
int main()
{
int i,j,n,ans;
scanf("%d",&n);
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
scanf("%d",&a[i][j]);
f[1][1]=a[1][1];
for(i=2;i<=n;i++)
for(j=1;j<=i;j++)
f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]; //状态转移方程
ans=0;
for(i=1;i<=n;i++) //max(f[n][j])
ans=max(ans,f[n][i]);
printf("%d",ans);
return 0;
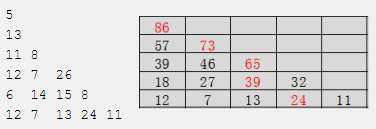
}方法2:逆推法
逆推时,f[i][j]的值从哪来?是从下面第 i+1 行的第 j 列和第 j+1 列来。状态转移方程为:
![f[i,j]=a[i][j]+max\left\{\begin{matrix} f[i+1][j]\\f[i+1][j+1] \end{matrix}\right.](http://img.inotgo.com/imagesLocal/202208/02/202208022000269923_0.gif)
边界:f[n][j]=a[n][j]。目标:f[1][1]。
【参考代码2】
#include <stdio.h>
#define MAXN 1010
int a[MAXN][MAXN]; //存储数塔数据
int f[MAXN][MAXN]; //f[i][j]表示从起点到i层j列的路径数字和
int max(int x,int y)
{
return x > y ? x : y;
}
int main()
{
int i,j,n;
scanf("%d",&n);
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
scanf("%d",&a[i][j]);
for(i=1;i<=n;i++)
f[n][i]=a[n][i];
for(i=n-1;i>=1;i--)
for(j=1;j<=i;j++)
f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j]; //状态转移方程
printf("%d",f[1][1]); //目标 f[1][1]
return 0;
}边栏推荐
猜你喜欢
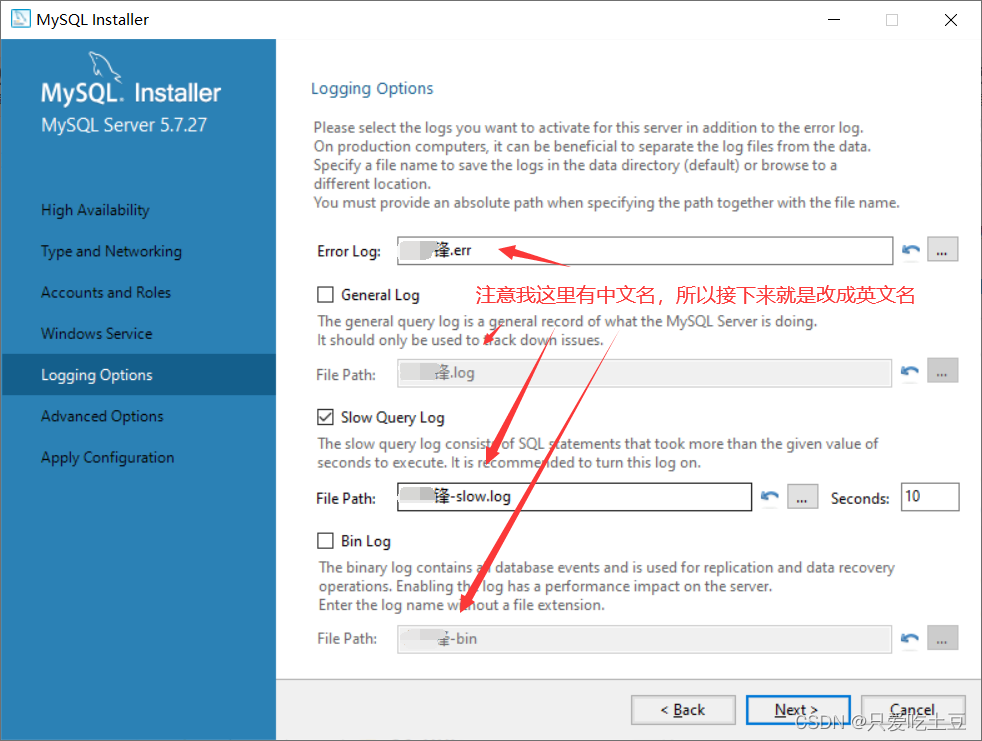
MySQL安装时一直卡在starting server

J9数字论:互联网跨链桥有什么作用呢?

实现fashion_minst服装图像分类

SCANIA SCANIA OTL tag is introduced
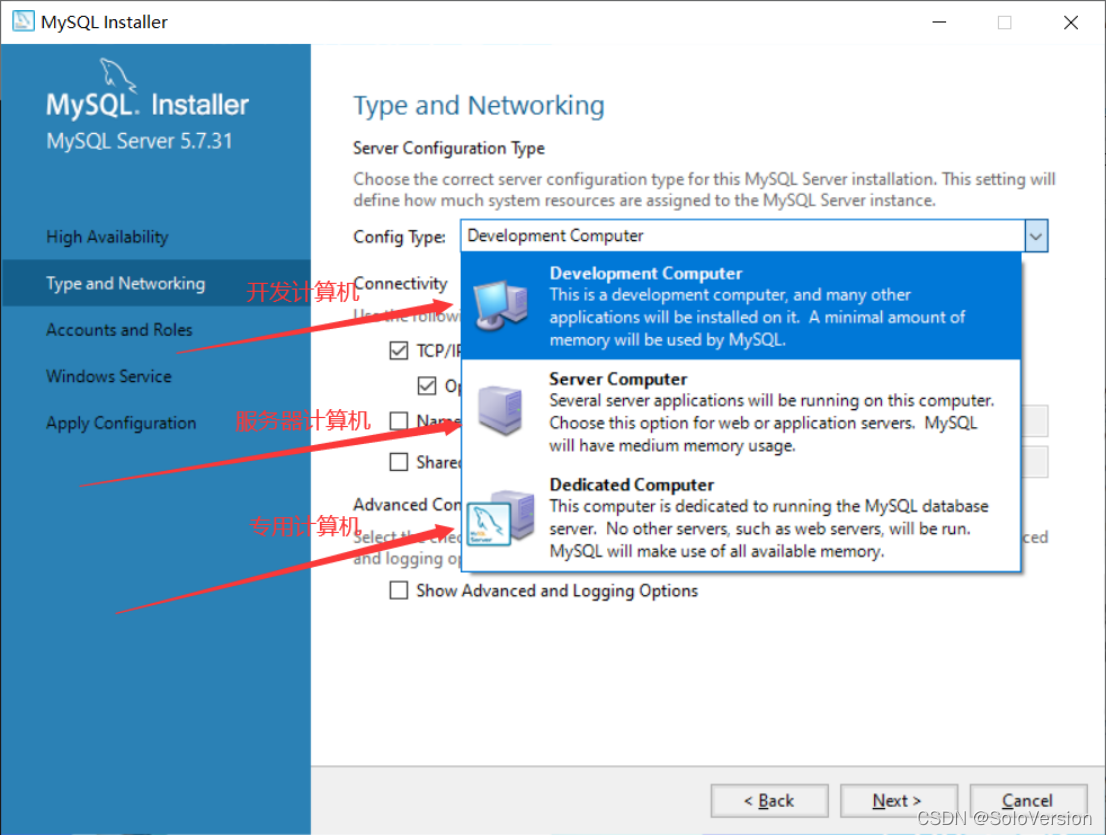
MySQL安装配置教程(超级详细、保姆级)

Thread线程类基本使用(下)
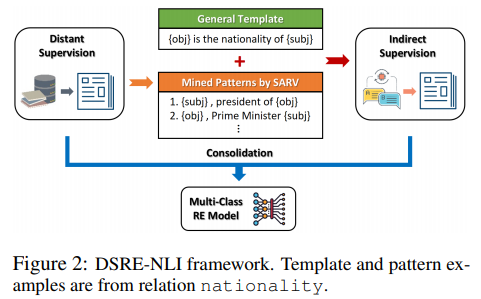
美国爱荷华州立大学| Improving Distantly Supervised Relation Extraction by Natural Language Inference(通过自然语言推理改进远程监督关系提取)

J9 Digital Currency Theory: Identifying Web3's New Scarcity: Open Source Developers
技术分享 | Apache Linkis 快速集成网页IDE工具 Scriptis

LM小型可编程控制器软件(基于CoDeSys)笔记二十五:plc的数据存储区(数字量输入通道部分)
随机推荐
GNN教程:图神经网络基础知识!
MySQL安装配置教程(超级详细、保姆级)
有效解决MySQL报错:ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: NO/YES)
【 LeetCode 】 1374. Generate each character string is an odd number
网络协议介绍
J9 Digital Currency Theory: Identifying Web3's New Scarcity: Open Source Developers
You want the metagenomics - microbiome knowledge in all the (2022.8)
ssdp协议搜索GB28181设备
【数据分析】:什么是数据分析?
ABAP语法小复习
KDD 2022 | 深度图神经网络中的特征过相关:一个新视角
B站HR对面试者声称其核心用户都是生活中的Loser
Office2021 安装MathType
Golang source code analysis: juju/ratelimit
磁盘分区的知识
网上那么多教人赚钱的方法,但是你实际上是靠什么赚钱的呢?
Golang source code analysis: time/rate
unittest自动化测试框架总结
ALV report learning summary
Solve the docker mysql can't write Chinese