当前位置:网站首页>Three gradient descent methods and code implementation
Three gradient descent methods and code implementation
2022-07-03 17:54:00 【Chen Chen】
Catalog
Preface
This paper belongs to Linear regression algorithm 【AIoT Stage three 】( Not updated yet ), Here is an excerpt from one of them , It is convenient for readers to understand and read quickly according to their needs . This paper deduces through formula + Both aspects of the code are carried out at the same time , Because it involves compiling and running the code , If you don't N u m P y NumPy NumPy, P a n d a s Pandas Pandas, M a t p l o t l i b Matplotlib Matplotlib The basis of , It is suggested to fix the article first : Data analysis three swordsmen 【AIoT Stage 1 ( Next )】( 100000 words blog post Nanny level explanation ), This paper is the second part of gradient descent , Before learning, you need to learn : gradient descent 【 Unconstrained optimization problems 】, There will be : Gradient descent optimization , Gradient descent optimization advanced ( Update yet )
1. Gradient descent method
1.1 The three gradients fall differently
There are three types of gradient descent : Batch gradient descent B G D BGD BGD(Batch Gradient Descent)、 Small batch gradient descent M B G D MBGD MBGD(Mini-Batch Gradient Descent)、 Stochastic gradient descent S G D SGD SGD(Stochastic Gradient Descent).

What is the difference between the three gradients ? Let's start with the gradient descent step , The gradient descent step is divided into the following four steps :
1、 Random assignment , R a n d o m Random Random Random number generation θ \theta θ, A random set of values w 0 、 w 1 … … w n w_0、w_1……w_n w0、w1……wn
2、 Find gradient g g g , The gradient represents the slope of the tangent at a point on the curve , Going down the tangent is equivalent to going down in the steepest direction of the slope
3、 i f if if g < 0 g < 0 g<0, θ \theta θ Bigger , i f if if g > 0 g > 0 g>0, θ \theta θ smaller
4、 Judge whether convergence or not c o n v e r g e n c e convergence convergence, If convergence jumps out of the iteration , If convergence is not achieved , Huidi 2 2 2 Step perform... Again 2 2 2 ~ 4 4 4 Step
The criterion of convergence is : As the iteration progresses, the loss function L o s s Loss Loss, The change is so small that it doesn't even change , That is, it is considered to reach convergence
The three gradients fall differently , Embodied in the second step :
B G D BGD BGD It means in Every iteration Use All samples To update the gradient
M B G D MBGD MBGD It means in Every iteration Use Part of the sample ( All samples 500 500 500 individual , Use among them 32 32 32 Samples ) To update the gradient
S G D SGD SGD Refer to Every iteration Random selection A sample To do gradient update
1.2 Linear regression gradient update formula
Review the previous formula !
The formula of the least square method is as follows :
J ( θ ) = 1 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2}\sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) - y^{(i)})^2 J(θ)=21i=1∑n(hθ(x(i))−y(i))2
Matrix writing :
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y) J(θ)=21(Xθ−y)T(Xθ−y)
Next, we will explain how to solve the problem of gradient descent 2 2 2 Step , That is, we need to derive the derivative of the loss function to .
θ j n + 1 = θ j n − η ∗ ∂ J ( θ ) ∂ θ j \theta_j^{n + 1} = \theta_j^{n} - \eta * \frac{\partial J(\theta)}{\partial \theta_j} θjn+1=θjn−η∗∂θj∂J(θ) among j j j It means the first one j j j A coefficient of
∂ J ( θ ) ∂ θ j = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 \frac{\partial J(\theta)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j}\frac{1}{2}(h_{\theta}(x) - y)^2 ∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2
= 1 2 ∗ 2 ( h θ ( x ) − y ) ∂ ∂ θ j ( h θ ( x ) − y ) = \frac{1}{2}*2(h_{\theta}(x) - y)\frac{\partial}{\partial \theta_j}(h_{\theta}(x) - y) =21∗2(hθ(x)−y)∂θj∂(hθ(x)−y) ( 1 ) (1) (1)
= ( h θ ( x ) − y ) ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = (h_{\theta}(x) - y)\frac{\partial}{\partial \theta_j}(\sum\limits_{i = 0}^n\theta_ix_i - y) =(hθ(x)−y)∂θj∂(i=0∑nθixi−y) ( 2 ) (2) (2)
= ( h θ ( x ) − y ) x j = (h_{\theta}(x) - y)x_j =(hθ(x)−y)xj ( 3 ) (3) (3)
x 2 x^2 x2 The derivative of is 2 x 2x 2x, According to the chain derivation rule , We can launch the first ( 1 ) (1) (1) Step . Then multiple linear regression , therefore h θ ( x ) h_{\theta}(x) hθ(x) Just yes θ T x \theta^Tx θTx That is w 0 x 0 + w 1 x 1 + … … + w n x n w_0x_0 + w_1x_1 + …… + w_nx_n w0x0+w1x1+……+wnxn namely ∑ i = 0 n θ i x i \sum\limits_{i = 0}^n\theta_ix_i i=0∑nθixi. Here we are right θ j \theta_j θj To find the partial derivative , So and w j w_j wj There is no negligible relationship , So there's only x j x_j xj.
We can conclude that θ j \theta_j θj Corresponding gradient and predicted value y ^ \hat{y} y^ And real value y y y of , here y ^ \hat{y} y^ and y y y Is a column vector ( That is, multiple data ), And also with θ j \theta_j θj Corresponding feature dimension x j x_j xj of , here x j x_j xj Is the second of the original dataset matrix j j j Column . If we separate each dimension θ 0 、 θ 1 … … θ n \theta_0、\theta_1……\theta_n θ0、θ1……θn Finding partial derivatives , The gradient values corresponding to all dimensions can be obtained .
- g 0 = ( h θ ( x ) − y ) x 0 g_0 = (h_{\theta}(x) - y)x_0 g0=(hθ(x)−y)x0
- g 1 = ( h θ ( x ) − y ) x 1 g_1 = (h_{\theta}(x) - y)x_1 g1=(hθ(x)−y)x1
- ……
- g j = ( h θ ( x ) − y ) x j g_j = (h_{\theta}(x) - y)x_j gj=(hθ(x)−y)xj
summary :
θ j n + 1 = θ j n − η ∗ ( h θ ( x ) − y ) x j \theta_j^{n + 1} = \theta_j^{n} - \eta * (h_{\theta}(x) - y )x_j θjn+1=θjn−η∗(hθ(x)−y)xj
1.3 Batch gradient descent B G D BGD BGD
Batch gradient descent method Is the most primitive form , It means in Every iteration Use All samples To update the gradient . The formula for updating parameters in each iteration is as follows :
θ j n + 1 = θ j n − η ∗ 1 n ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{n}\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗n1i=1∑n(hθ(x(i))−y(i))xj(i)
Get rid of 1 n \frac{1}{n} n1 It's fine too , Because it's a constant , You can talk to η \eta η Merge
θ j n + 1 = θ j n − η ∗ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\sum\limits_{i = 1}^{n} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗i=1∑n(hθ(x(i))−y(i))xj(i)
Matrix writing :
θ n + 1 = θ n − η ∗ X T ( X θ − y ) \theta^{n + 1} = \theta^{n} - \eta * X^T(X\theta -y) θn+1=θn−η∗XT(Xθ−y)
among 𝑖 = 1 , 2 , . . . , n 𝑖 = 1, 2, ..., n i=1,2,...,n Represents the number of samples , 𝑗 = 0 , 1 … … 𝑗 = 0, 1…… j=0,1…… The number of features , Here we use the offset term , I.e. solution x 0 ( i ) = 1 x_0^{(i)} = 1 x0(i)=1.
Note that there is a summation function when updating here , That is to calculate and process all samples !
advantage :
(1) One iteration is to compute all samples , At this point, the matrix is used to operate , Parallel .
(2) The direction determined by the whole data set can better represent the sample population , So that we can be more accurate in the direction of the extremum . When the objective function is convex , B G D BGD BGD We must be able to get the global optimum .
shortcoming :
(1) When the number of samples n n n When a large , Each iteration step needs to be calculated for all samples , The training process will be slow .
In terms of the number of iterations , B G D BGD BGD The number of iterations is relatively small . The convergence curve of its iteration can be shown as follows :
1.4 Stochastic gradient descent S G D SGD SGD
Random gradient descent method Different from batch gradient descent , The random gradient descent is Every iteration Use A sample To update the parameters . Make training faster . The formula for updating parameters in each iteration is as follows :
θ j n + 1 = θ j n − η ∗ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *(h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗(hθ(x(i))−y(i))xj(i)
Batch gradient descent The algorithm will be used every time All The training sample , So these calculations are redundant , Because the same sample set is used every time . and Stochastic gradient descent The algorithm only selects randomly at a time One Samples to update model parameters , So every time you learn, you are very fast .
advantage :
(1) Because it is not an updated calculation on all training data , But in each iteration , Randomly select a piece of data for update calculation , In this way, the update speed of each round of parameters is greatly accelerated .
shortcoming :
(1) Decreased accuracy . Because even if the objective function is strongly convex , S G D SGD SGD Still can't converge linearly .
(2) It may converge to the local optimum , Because a single sample can't represent the trend of the whole sample .
Explain why SGD Convergence rate ratio BGD Be quick :
- Here we assume that 30 W 30W 30W Samples , about B G D BGD BGD for , Each iteration requires calculation 30 W 30W 30W Only samples can update the parameters once , It may take many iterations to get the minimum value ( So let's say that this is 10 10 10).
- And for S G D SGD SGD, Only one sample is required for each parameter update , So if you use this 30W Samples for parameter update , Then the parameters will be iterated 30 W 30W 30W Time , And in the meantime , S G D SGD SGD It can ensure that it can converge to a suitable minimum .
- in other words , In convergence , B G D BGD BGD To calculate the 10 × 30 W 10×30W 10×30W Time , and S G D SGD SGD Only calculated 1 × 30 W 1×30W 1×30W Time .
In terms of the number of iterations , S G D SGD SGD More iterations , The search process in solution space will be blind . The convergence curve of its iteration can be shown as follows :

1.5 Small batch gradient descent M B G D MBGD MBGD
Small batch gradient descent , It is an example of batch gradient descent and random gradient descent compromise Way . The idea is : Every iteration Use a portion of the total sample ( b a t c h s i z e ) (batch_size) (batchsize) Samples to update parameters . So let's assume that b a t c h s i z e = 20 batch_size = 20 batchsize=20, Sample size n = 1000 n = 1000 n=1000 . The balance between update speed and update times is achieved . The formula for updating parameters in each iteration is as follows :
θ j n + 1 = θ j n − η ∗ 1 b a t c h _ s i z e ∑ i = 1 b a t c h _ s i z e ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{n + 1} = \theta_j^{n} - \eta *\frac{1}{batch\_size}\sum\limits_{i = 1}^{batch\_size} (h_{\theta}(x^{(i)}) - y^{(i)} )x_j^{(i)} θjn+1=θjn−η∗batch_size1i=1∑batch_size(hθ(x(i))−y(i))xj(i)
Relative to random gradient descent algorithm , The small batch gradient descent algorithm reduces the convergence volatility , That is to say, the variance of parameter update is reduced , Make updates more stable . The gradient decreases relative to the total amount , It improves the speed of each learning . And it doesn't need to worry about the memory bottleneck, so it can use matrix operation to calculate efficiently .
In general , Small batch gradient descent is the recommended variant of gradient descent , Especially in deep learning . Choose... Randomly every time 2 2 2 Idempotent number of samples to learn , for example : 8 8 8、 16 16 16、 32 32 32、 64 64 64、 128 128 128、 256 256 256. Because the structure of computer is binary . But you have to choose according to the specific problem , Many tests can be carried out in practice , Select a number of samples with appropriate update speed and times .
M B G D MBGD MBGD The convergence curve of gradient descent iteration is more gentle :

2. Code implementation gradient descent
2.1 Batch gradient descent B G D BGD BGD
2.1.1 Univariate linear regression
import numpy as np
# Create data
X = np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size = 2)
# Increase noise , Also known as " Add salt "
y = w * X + b + np.random.rand(100, 1)
# hold b As a bias term , Intercept correspondence coefficient x_0 = 1, to update X
X = np.concatenate([X, np.full(shape = (100, 1),
fill_value = 1)], axis = 1)
# cycles
epoches = 10000
# Learning rate
eta = 0.01
# Coefficient of required solution ," Blind "
theta = np.random.randn(2, 1)
for i in range(epoches):
# Batch gradient descent ,X For matrix , Contains all the data
g = X.T.dot(X.dot(theta) - y) # The gradient calculated according to the formula
theta = theta - eta * g
print(' True slope 、 intercept :', w, b)
print(' Use BGD Find the slope of 、 intercept :', theta[0], theta[1])
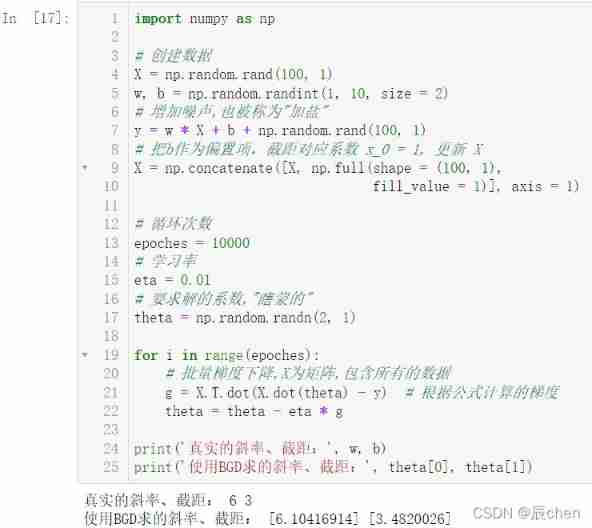
It can be seen that , There is still a certain gap between our calculated data and the real data , This is adding noise ( Add salt ) The result of the action of , But such calculation data is more real , Because data in real life cannot be perfect .
The following figure is a schematic diagram of gradient descent :
We can see that , For the beginning of gradient descent , L e a r n i n g Learning Learning s t e p step step The larger , That is, the value of learning rate is relatively large , The closer you get to the right answer , L e a r n i n g Learning Learning s t e p step step The smaller it becomes , This actually gives us an idea , That our e t a eta eta It can change dynamically with the number of cycles that the gradient decreases :
import numpy as np
# Create data
X = np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size = 2)
# Increase noise , Also known as " Add salt "
y = w * X + b + np.random.rand(100, 1)
# hold b As a bias term , Intercept correspondence coefficient x_0 = 1, to update X
X = np.concatenate([X, np.full(shape = (100, 1),
fill_value = 1)], axis = 1)
# cycles
epoches = 10000
# Learning rate
t0, t1 = 5, 1000
# t Is the number of gradient drops , Inverse time attenuation , As the gradient decreases, the number of times increases , The learning rate is getting smaller
def learning_rate_shedule(t):
return t0 / (t + t1)
# Coefficient of required solution ," Blind "
theta = np.random.randn(2, 1)
for i in range(epoches):
# Batch gradient descent ,X For matrix , Contains all the data
g = X.T.dot(X.dot(theta) - y) # The gradient calculated according to the formula
eta = learning_rate_shedule(i)
theta = theta - eta * g
print(' True slope 、 intercept :', w, b)
print(' Use BGD Find the slope of 、 intercept :', theta[0], theta[1])

2.1.2 Eight variable linear regression
import numpy as np
# Create data
X = np.random.rand(100, 8)
w = np.random.randint(1, 10, size = (8, 1))
b = np.random.randint(1, 10, size = 1)
# Increase noise , Also known as " Add salt "
y = X.dot(w) + b + np.random.rand(100, 1)
# hold b As a bias term , Intercept correspondence coefficient x_0 = 1, to update X
X = np.concatenate([X, np.full(shape = (100, 1),
fill_value = 1)], axis = 1)
# cycles
epoches = 10000
# Learning rate
t0, t1 = 5, 1000
# t Is the number of gradient drops , Inverse time attenuation , As the gradient decreases, the number of times increases , The learning rate is getting smaller
def learning_rate_shedule(t):
return t0 / (t + t1)
# Coefficient of required solution ," Blind "
theta = np.random.randn(9, 1)
for i in range(epoches):
# Batch gradient descent ,X For matrix , Contains all the data
g = X.T.dot(X.dot(theta) - y) # The gradient calculated according to the formula
eta = learning_rate_shedule(i)
theta = theta - eta * g
print(' True slope 、 intercept :', w, b)
print(' Use BGD Find the slope of 、 intercept :', theta)

2.2 Stochastic gradient descent S G D SGD SGD
2.2.1 Univariate linear regression
import numpy as np
# Create data
X = np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size = 2)
# Increase noise , Also known as " Add salt "
y = w * X + b + np.random.rand(100, 1)
# hold b As a bias term , Intercept correspondence coefficient x_0 = 1, to update X
X = np.concatenate([X, np.full_like(X, fill_value = 1)], axis = 1)
# cycles
epoches = 100
# Learning rate
t0, t1 = 5, 1000
# t Is the number of gradient drops , Inverse time attenuation , As the gradient decreases, the number of times increases , The learning rate is getting smaller
def learning_rate_shedule(t):
return t0 / (t + t1)
theta = np.random.randn(2, 1)
cnt = 0 # Indicates the number of workouts
for t in range(epoches):
index = np.arange(100)
np.random.shuffle(index) # Shuffle , Out of order
# NumPy Fancy index
X = X[index]
y = y[index]
for i in range(100):
X_i = X[[i]]
y_i = y[[i]]
# According to this sample , Calculate the gradient
g = X_i.T.dot(X_i.dot(theta) - y_i)
eta = learning_rate_shedule(cnt)
cnt += 1
theta -= eta * g
print(' True slope 、 intercept :', w, b)
print(' Use SGD Find the slope of 、 intercept :', theta[0], theta[1])

2.2.2 Five variable linear regression
import numpy as np
# Create data
X = np.random.rand(100, 5)
w = np.random.randint(1, 10, size = (5, 1))
b = np.random.randint(1, 10, size = 1)
# Increase noise , Also known as " Add salt "
y = X.dot(w) + b + np.random.rand(100, 1)
# hold b As a bias term , Intercept correspondence coefficient x_0 = 1, to update X
X = np.concatenate([X, np.full(shape = (100, 1), fill_value = 1)], axis = 1)
# cycles
epoches = 100
# Learning rate
t0, t1 = 5, 1000
# t Is the number of gradient drops , Inverse time attenuation , As the gradient decreases, the number of times increases , The learning rate is getting smaller
def learning_rate_shedule(t):
return t0 / (t + t1)
theta = np.random.randn(6, 1)
cnt = 0 # Indicates the number of workouts
for t in range(epoches):
index = np.arange(100)
np.random.shuffle(index) # Shuffle , Out of order
# NumPy Fancy index
X = X[index]
y = y[index]
for i in range(100):
X_i = X[[i]] # Two []: You can do matrix operations
y_i = y[[i]]
# According to this sample , Calculate the gradient
g = X_i.T.dot(X_i.dot(theta) - y_i)
eta = learning_rate_shedule(cnt)
cnt += 1
theta -= eta * g
print(' True slope 、 intercept :', w, b)
print(' Use SGD Find the slope of 、 intercept :', theta)

2.3 Small batch gradient descent M B G D MBGD MBGD
2.3.1 Univariate linear regression
import numpy as np
# 1、 Create a dataset X,y
X = np.random.rand(100, 1)
w,b = np.random.randint(1, 10,size = 2)
y = w * X + b + np.random.randn(100, 1)
# 2、 Use offset x_0 = 1, to update X
X = np.c_[X, np.ones((100, 1))]
# 3、 Define a function to adjust the learning rate
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t + t1)
# 4、 Create a super parameter round 、 Number of samples 、 Small batch quantity
epochs = 100
n = 100
batch_size = 16
num_batches = int(n / batch_size)
# 5、 initialization W0...Wn, Standard Zhengtai distribution creates W
θ = np.random.randn(2, 1)
# 6、 many times for Loop to achieve gradient descent , The final result converges
for epoch in range(epochs):
# On the double deck for Between cycles , Disrupt the data index order before each round starts the batch iteration
index = np.arange(n)
np.random.shuffle(index)
X = X[index]
y = y[index]
for i in range(num_batches):
# Take one batch of data at a time 16 Samples
X_batch = X[i * batch_size : (i + 1) * batch_size]
y_batch = y[i * batch_size : (i + 1) * batch_size]
g = X_batch.T.dot(X_batch.dot(θ) - y_batch)
learning_rate = learning_rate_schedule(epoch * n + i)
θ = θ - learning_rate * g
print(' The true slope and intercept are :', w, b)
print(' The slope and intercept of gradient descent calculation are :',θ)

2.3.2 Ternary linear regression
import numpy as np
# 1、 Create a dataset X,y
X = np.random.rand(100, 3)
w = np.random.randint(1,10,size = (3, 1))
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)
# 2、 Use offset X_0 = 1, to update X
X = np.c_[X, np.ones((100, 1))]
# 3、 Define a function to adjust the learning rate
t0, t1 = 5, 500
def learning_rate_schedule(t):
return t0/(t + t1)
# 4、 Create a super parameter round 、 Number of samples 、 Small batch quantity
epochs = 10000
n = 100
batch_size = 16
num_batches = int(n / batch_size)
# 5、 initialization W0...Wn, Standard Zhengtai distribution creates W
θ = np.random.randn(4, 1)
# 6、 many times for Loop to achieve gradient descent , The final result converges
for epoch in range(epochs):
# On the double deck for Between cycles , Disrupt the data index order before each round starts the batch iteration
index = np.arange(n)
np.random.shuffle(index)
X = X[index]
y = y[index]
for i in range(num_batches):
# Take one batch of data at a time 16 Samples
X_batch = X[i * batch_size : (i + 1) * batch_size]
y_batch = y[i * batch_size : (i + 1) * batch_size]
g = X_batch.T.dot(X_batch.dot(θ) - y_batch)
learning_rate = learning_rate_schedule(epoch * n + i)
θ = θ - learning_rate * g
print(' The true slope and intercept are :', w, b)
print(' The slope and intercept of gradient descent calculation are :',θ)

边栏推荐
- PHP processing - watermark images (text, etc.)
- Leetcode 669 pruning binary search tree -- recursive method and iterative method
- Applet with multiple tabs and Swipers + paging of each tab
- WEB-UI自动化测试-最全元素定位方法
- [Tongxin UOS] scanner device management driver installation
- 聊聊支付流程的設計與實現邏輯
- [combinatorics] generating function (shift property)
- [combinatorics] recursive equation (case where the non-homogeneous part is exponential | example where the non-homogeneous part is exponential)
- Introduction to PHP MySQL
- supervisor监控Gearman任务
猜你喜欢

IntelliJ 2021.3 short command line when running applications

Tensorboard quick start (pytoch uses tensorboard)
Hongmeng fourth training

Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
Talk about the design and implementation logic of payment process

TensorBoard快速入门(Pytorch使用TensorBoard)

基于人脸识别的课堂考勤系统 tkinter+openpyxl+face_recognition
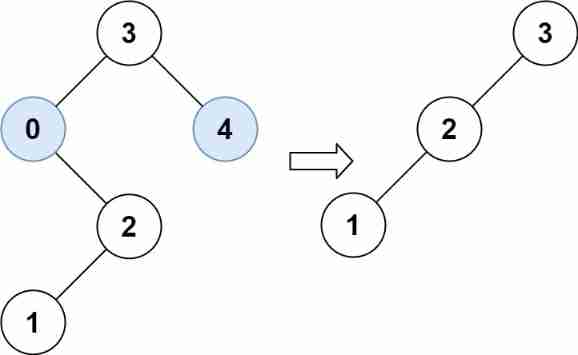
Leetcode 669 pruning binary search tree -- recursive method and iterative method

Type conversion, variable
MySQL grouping query
随机推荐
Hongmeng fourth training
Micro service component sentinel console call
QT learning diary 9 - dialog box
Line by line explanation of yolox source code of anchor free series network (5) -- mosaic data enhancement and mathematical understanding
Hongmeng third training
Kotlin的协程:上下文
Research Report on investment trends and development planning of China's thermal insulation material industry, 2022-2028
国内如何购买Google Colab会员
BFS - topology sort
Fedora 21 installs lamp host server
[combinatorics] generating function (shift property)
PHP MySQL inserts multiple pieces of data
(9) Opencv Canny edge detection
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
Leetcode 669 pruning binary search tree -- recursive method and iterative method
Internet Hospital his Management Platform source, online Inquiry, appointment Registration Smart Hospital Small program source
Postfix 技巧和故障排除命令
聊聊支付流程的设计与实现逻辑
OpenSSL的SSL/BIO_get_fd
STM32实现74HC595控制