当前位置:网站首页>[combinatorics] recursive equation (case where the non-homogeneous part is exponential | example where the non-homogeneous part is exponential)
[combinatorics] recursive equation (case where the non-homogeneous part is exponential | example where the non-homogeneous part is exponential)
2022-07-03 17:23:00 【Programmer community】
List of articles
- One 、 The non-homogeneous part is exponential
- Two 、 The non-homogeneous part is exponential Example
One 、 The non-homogeneous part is exponential
Linear Nonhomogeneous recurrence equation with constant coefficients :
H
(
n
)
−
a
1
H
(
n
−
1
)
−
⋯
−
a
k
H
(
n
−
k
)
=
f
(
n
)
H(n) - a_1H(n-1) - \cdots - a_kH(n-k) = f(n)
H(n)−a1H(n−1)−⋯−akH(n−k)=f(n) ,
n
≥
k
,
a
k
≠
0
,
f
(
n
)
≠
0
n\geq k , a_k\not= 0, f(n) \not= 0
n≥k,ak=0,f(n)=0
The left side of the above equation And “ Linear homogeneous recurrence equation with constant coefficients ” It's the same , But not on the right
0
0
0 , It's based on
n
n
n Of function
f
(
n
)
f(n)
f(n) , This type of recursive equation is called “ Linear Nonhomogeneous recurrence equation with constant coefficients ” ;
The non-homogeneous part is exponential :
If the above “ Linear Nonhomogeneous recurrence equation with constant coefficients ” Of Nonhomogeneous part
f
(
n
)
f(n)
f(n) It's an exponential function ,
β
n
\beta^n
βn ,
If
β
\beta
β Not a characteristic root ,
Then the special solution form of the nonhomogeneous part is :
H
∗
(
n
)
=
P
β
n
H^*(n) = P\beta^n
H∗(n)=Pβn ,
P
P
P Is constant ;
The above special solution
H
∗
(
n
)
=
P
β
n
H^*(n) = P\beta^n
H∗(n)=Pβn , Into the recursive equation , Solve the constant
P
P
P Value , Then the complete special solution is obtained ;
“ Linear Nonhomogeneous recurrence equation with constant coefficients ” The general solution is
H
(
n
)
=
H
(
n
)
‾
+
H
∗
(
n
)
H(n) = \overline{H(n)} + H^*(n)
H(n)=H(n)+H∗(n)
Use the above solution Special solution , And recurrence equation General solution of homogeneous part , Form the complete general solution of the recursive equation ;
Two 、 The non-homogeneous part is exponential Example
Recurrence equation :
a
n
=
6
a
n
−
1
+
8
n
−
1
a_n = 6a_{n-1} + 8^{n-1}
an=6an−1+8n−1
initial value :
a
1
=
7
a_1=7
a1=7
First step , First solve the recursive equation Special solutions corresponding to Nonhomogeneous parts ,
The standard form of recurrence equation is :
a
n
−
6
a
n
−
1
=
8
n
−
1
a_n - 6a_{n-1} = 8^{n-1}
an−6an−1=8n−1
The nonhomogeneous part is
8
n
−
1
8^{n-1}
8n−1 ,
Therefore, its Special solution The form of
a
∗
n
=
P
8
n
−
1
a^*n = P 8^{n-1}
a∗n=P8n−1 , among
P
P
P Is constant ;
The special solution is substituted into the above recursive equation :
P
8
n
−
1
−
6
P
8
n
−
2
=
8
n
−
1
P 8^{n-1} - 6P 8^{n-2} = 8^{n-1}
P8n−1−6P8n−2=8n−1
stay
6
P
8
n
−
2
6P 8^{n-2}
6P8n−2 Item times
8
8
8 become
6
P
8
n
−
1
6P8^{n-1}
6P8n−1 , Divided by
8
8
8 become
6
P
8
n
−
1
8
=
3
P
8
n
−
1
4
\cfrac{6P8^{n-1}}{8}=\cfrac{3P8^{n-1}}{4}
86P8n−1=43P8n−1 , Into the equation ,
P
8
n
−
1
−
3
P
8
n
−
1
4
=
8
n
−
1
P 8^{n-1} - \cfrac{3P8^{n-1}}{4} = 8^{n-1}
P8n−1−43P8n−1=8n−1
P
8
n
−
1
4
=
8
n
−
1
\cfrac{P8^{n-1}}{4} = 8^{n-1}
4P8n−1=8n−1
P
4
=
1
\cfrac{P}{4} = 1
4P=1
P
=
4
P = 4
P=4
The constant term in the special solution
P
=
4
P=4
P=4 , The final solution is
a
∗
n
=
4
×
8
n
−
1
a^*n = 4\times 8^{n-1}
a∗n=4×8n−1
The second step , Find the general solution of the homogeneous part
The standard form of recurrence equation is :
a
n
−
6
a
n
−
1
=
8
n
−
1
a_n - 6a_{n-1} = 8^{n-1}
an−6an−1=8n−1 ,
Homogeneous part is
a
n
−
6
a
n
−
1
=
0
a_n - 6a_{n-1} = 0
an−6an−1=0
Write the characteristic equation :
x
−
6
=
0
x - 6 = 0
x−6=0 ,
Characteristic root
q
=
6
q= 6
q=6
Write the homogeneous partial general solution form :
a
n
‾
=
c
×
6
n
\overline{a_n} = c \times 6^n
an=c×6n
“ Linear Nonhomogeneous recurrence equation with constant coefficients ” The general solution is
a
n
=
a
n
‾
+
a
∗
n
a_n = \overline{a_n} + a^*n
an=an+a∗n
The general solution of the recurrence equation is :
a
n
=
c
×
6
n
+
4
×
8
n
−
1
a_n = c \times 6^n + 4\times 8^{n-1}
an=c×6n+4×8n−1
The third step , Substitute into the initial value , Find the final general solution
Substitute into the initial value
a
1
=
7
a_1 = 7
a1=7 Get from the above general solution
c
×
6
1
+
4
×
8
1
−
1
=
7
c \times 6^1 + 4 \times 8^{1-1} = 7
c×61+4×81−1=7
6
c
+
4
=
7
6c + 4 = 7
6c+4=7
c
=
1
2
c=\cfrac{1}{2}
c=21
a
n
=
c
×
6
n
+
4
×
8
n
−
1
a_n = c \times 6^n + 4\times 8^{n-1}
an=c×6n+4×8n−1 Constants in the general solution
c
=
1
2
c=\cfrac{1}{2}
c=21 , Substitute constants into ,
The general explanation is
a
n
=
1
2
×
6
n
+
4
×
8
n
−
1
a_n = \cfrac{1}{2} \times 6^n + 4\times 8^{n-1}
an=21×6n+4×8n−1
边栏推荐
- C language modifies files by line
- [combinatorics] recursive equation (the relationship theorem between the solution of the recursive equation and the characteristic root | the linear property theorem of the solution of the recursive e
- 聊聊接口优化的几个方法
- Rsync remote synchronization
- Talk about several methods of interface optimization
- ANOVA example
- One brush 149 force deduction hot question-10 regular expression matching (H)
- Hongmeng third training
- Test your trained model
- 鸿蒙第三次培训
猜你喜欢
One brush 147-force deduction hot question-4 find the median of two positive arrays (H)

Select 3 fcpx plug-ins. Come and see if you like them

Wechat applet for the first time

Pools de Threads: les composants les plus courants et les plus sujets aux erreurs du Code d'affaires
kubernetes资源对象介绍及常用命令(五)-(NFS&PV&PVC)

设计电商秒杀

【RT-Thread】nxp rt10xx 设备驱动框架之--hwtimer搭建和使用
Depth first search of graph
免费数据 | 新库上线 | CnOpenData中国保险中介机构网点全集数据
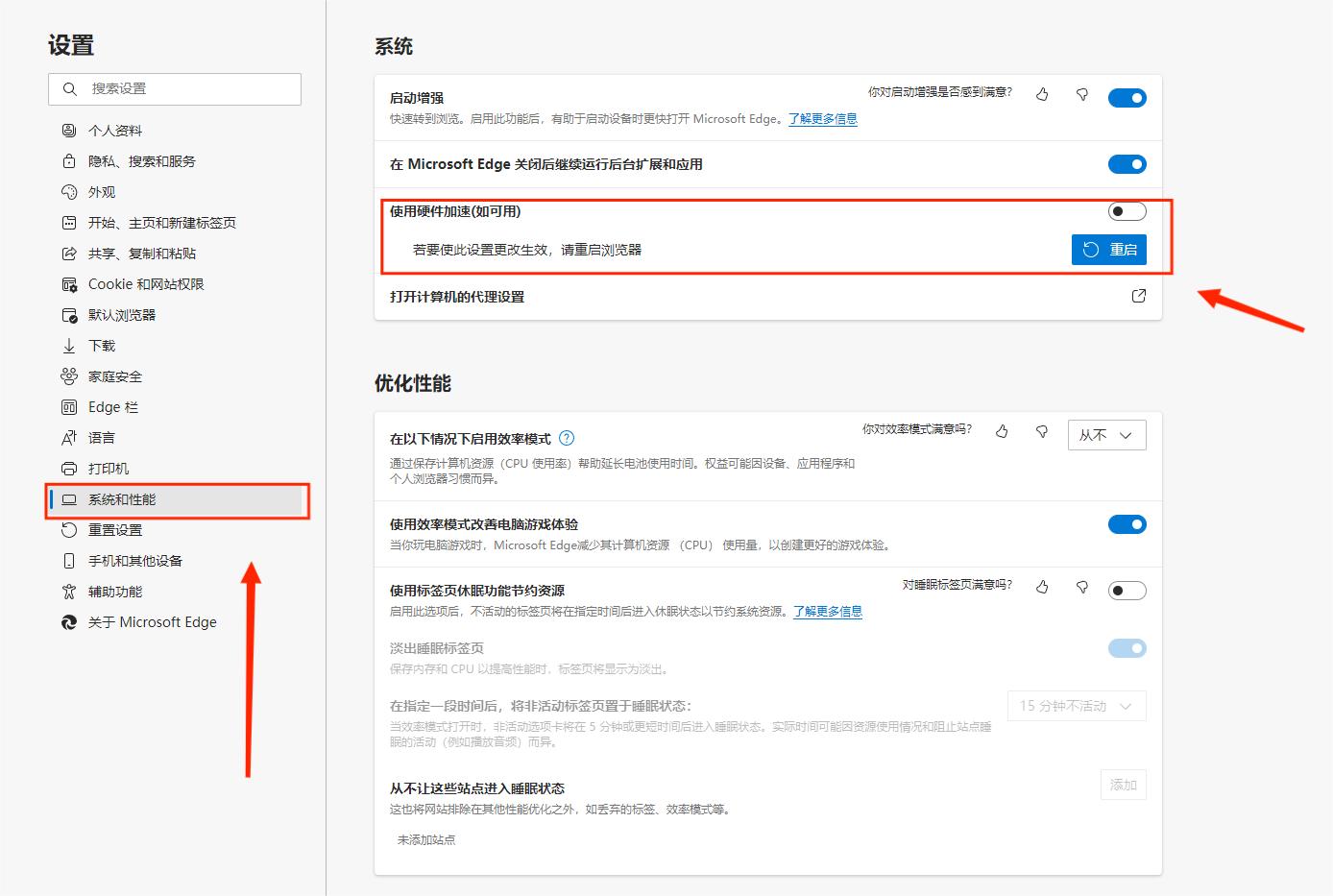
Notes on problems -- watching videos on edge will make the screen green
随机推荐
AcWing 3438. 数制转换
鸿蒙第三次培训
PR second time
Is AI too slow to design pictures and draw illustrations? 3 sets of practical brushes to save you
27. Input 3 integers and output them in descending order. Pointer method is required.
简单配置PostFix服务器
Pools de Threads: les composants les plus courants et les plus sujets aux erreurs du Code d'affaires
VM11289 WAService. js:2 Do not have __ e handler in component:
Where is the database account used when running SQL tasks in data warehouse tasks configured
LeetCode13.罗马数字转整数(三种解法)
Thread pool: the most common and error prone component of business code
29: Chapter 3: develop Passport Service: 12: develop [obtain user account information, interface]; (use VO class to package the found data to meet the requirements of the interface for the returned da
One brush 149 force deduction hot question-10 regular expression matching (H)
How to train mask r-cnn model with your own data
Online assignment 3 of mobile Internet technology in the 20th autumn of electronic technology [standard answer]
How SVN views modified file records
Redis: operation commands for list type data
Enterprise custom form engine solution (XI) -- form rule engine 1
Financial management (Higher Vocational College) financial management online Assignment 1 in autumn 20
When absolutely positioned, the element is horizontally and vertically centered