One brush 147-force deduction hot question-4 find the median of two positive arrays (H)

 subject ：
 Given two sizes, they are  m  and  n  Positive order of （ From small to large ） Array  nums1  and  nums2.
 Please find and return the values of these two positive ordered arrays   Median  

 The time complexity of the algorithm should be  O(log (m+n)) .
---------------------
 Example ：
 Input ：nums1 = [1,3], nums2 = [2]
 Output ：2.00000
 explain ： Merge array  = [1,2,3] , Median  2
 Example  2：

 Input ：nums1 = [1,2], nums2 = [3,4]
 Output ：2.50000
 explain ： Merge array  = [1,2,3,4] , Median  (2 + 3) / 2 = 2.5
 
 Tips ：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
-------------------
 reflection ：
 Time complexity see  log, Obviously , We can only use the dichotomy method to achieve .
 We might as well use another way of thinking , The question is to find the median , It's actually asking for the first  k  A special case of decimals , But for the second  k  There is an algorithm for decimals .
 Because the sequence is ordered , In fact, we can exclude half of them .
 Suppose we're looking for the third  k  decimal , We can eliminate each cycle  k/2  Number . Look at the next example .

 Suppose we're looking for the third  7  Small numbers .

 We compare the second... Of the two arrays  k/2  A digital , If  k  Is odd , Rounding down .
 That is to compare the second  3  A digital , In the upper array  4  And... In the lower array  3, If which one is small ,
 Just before that array  k/2  It's not the number one  k  Small number , So you can rule out .
 That is to say  1,2,3  These three numbers can't be the third  7  Small numbers , We can rule it out .
 take  1349  and  45678910  Compare the two arrays as a new array .

 More generally  A[1] ,A[2] ,A[3],A[k/2] ... ,B[1],B[2],B[3],B[k/2] ... ,
 If  A[k/2]<B[k/2] , that A[1],A[2],A[3],A[k/2] It can't be the second  k  Small numbers .

A  The array is smaller than  A[k/2]  Small numbers have  k/2-1  individual ,
B  Array ,B[k/2]  Than  A[k/2]  Small ,
 hypothesis  B[k/2]  The numbers in front are better than  A[k/2]  Small , There is only a  k/2-1  individual ,
 So than  A[k/2]  Small numbers have at most  k/1-1+k/2-1=k-2 individual ,
 therefore  A[k/2]  It's the... At most  k-1  Small number . And than  A[k/2]  A small number is even less likely to be the number  k  Small number , So you can exclude them .

 The orange part indicates the number that has been removed .

 Because we have ruled out  3  A digital , This is the  3  The number must be at the top ,
 So in two new arrays , We just need to find the first  7 - 3 = 4  Just a small number , That is to say  k = 4.
 At this point, two arrays , Compare the first  2  A digital ,3 < 5, So we can put... In the small array  1 ,3  Get rid of .

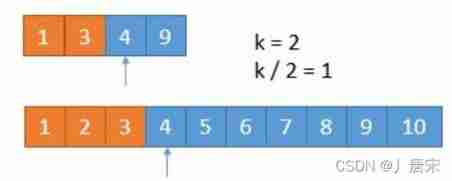
 We ruled out  2  A digital , So now find the first  4 - 2 = 2  Just a small number .
 At this point, the... Of the two arrays is compared  k / 2 = 1  Number ,4 == 4,
 What shall I do? ？ Because the two numbers are equal , So no matter which array we remove ,
 Because get rid of  1  One will always keep  1  One of the , So it doesn't affect .
 In order to unify , Let's assume  4 > 4  Well , So at this time, the following  4  Get rid of .

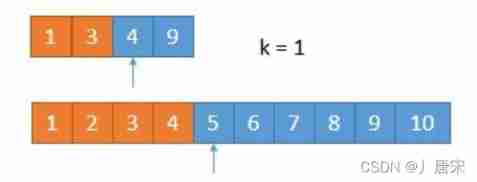
 Due to the removal of  1  A digital , At this point, we are looking for the third  1  Small numbers , the 
 You just need to judge which number is smaller in the first two arrays , That is to say  4.
 So the first  7  The small number is  4.

 We always take  k/2  Compare the number of , Sometimes you may encounter an array with a length less than  k/2 When .

 here  k / 2  be equal to  3, And the length of the upper array is  2, Let's just point the arrow to the end of it .
 In this case , because  2 < 3, So it will lead to the upper array  1,2  Are excluded . Cause the following situation .

 because  2  Elements are excluded , So at this time  k = 5,
 And because the array above is empty , We just need to return the... Of the lower array  5  Just a number .

 You can see from the top , Whether it's looking for the odd or even number , It has no effect on our algorithm ,
 And in the process of algorithm ,k  The value of can change from odd to even , Will eventually become  1  Or because an array is empty , Direct return .

 So we use the idea of recursion ,
 To prevent the array length from being less than  k/2, So every comparison  min(k/2,len( Array )  Corresponding number ,
 Exclude the number of the small corresponding array , Put two new arrays into recursion , and 
 And  k  To subtract the number of excluded numbers . Recursive exit is when  k=1  Or one of the numbers is... Long  0  了 .
 Code ：
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    
    int n = nums1.length;
    int m = nums2.length;
    // Because the array is indexed 0 At the beginning , So we have to +1, Index (k+1) Number of numbers , That's the number one k Number .
    int left = (n + m + 1) / 2;
    int right = (n + m + 2) / 2;
    // Combine even and odd numbers , If it's odd , Will ask for the same twice  k .
    return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) 
    			+ getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;  
}
    
    private int getKth(int[] nums1, int start1, int end1, 
    					int[] nums2, int start2, int end2, int k) {
    
    	// Because index and arithmetic are different 6-0=6, But there is a 7 The number of , because end The initial is the array length -1 Composed of .
        // Last len Represents the current array ( It may also be an array after recursive exclusion ), The number of elements that meet the current condition 
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        // Give Way  len1  The length of is less than  len2, This ensures that if an array is empty , It must be  len1 
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        // If there are no elements in an array , That is, from the remaining array nums2 Actually start2 Start adding k Again -1.
        // because k Represents the number of , Not the index , So from nums2 I'll look for it later k Number , That is start2 + k-1 Just at the index .
        // Because it also includes nums2[start2] It's also a number . Because it was not excluded in the last iteration 
        if (len1 == 0) return nums2[start2 + k - 1];
		// If k=1, It shows that it is closest to the median , That is, in two arrays start Index , Who's worth less , The median is who 
		//(start The index indicates the unqualified elements that have been eliminated after iteration ,
		// That is, the logical range of the array that has not been discarded is nums[start]--->nums[end]).
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);
		 // To prevent the array length from being less than  k/2, Each comparison will grow from the current array and k/2 The comparison ,
		 // Take the small one ( If the larger one , The array will be out of bounds )
        // Then the prime group if len1 Less than k / 2, Indicates that the array will reach the end after the next traversal ,
        // Then we will find the median in the remaining array 
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;
		// If nums1[i] > nums2[j], Express nums2 The array contains j Indexes , Previous elements , Logically, all are eliminated ,
		// That is, next time from J+1 Start .
        // and k It becomes k - (j - start2 + 1), That is, subtract the number of logically discharged elements 
        //( To add 1, Because the indexes are subtracted , Compared with the actual exclusion, there is one less )
        if (nums1[i] > nums2[j]) {
    
            return getKth(nums1, start1, end1, nums2, j + 1, 
            			end2, k - (j - start2 + 1));
        }
        else {
    
            return getKth(nums1, i + 1, end1, nums2, start2, 
            				end2, k - (i - start1 + 1));
        }
    }
 Time complexity ： Every time you do a cycle , We will reduce  k/2  Elements ,
 So time complexity is  O(log(k), and  k=(m+n)/2, So the final complexity is  O(log(m+n）.

 Spatial complexity ： Although we use recursion , But you can see that this recursion belongs to tail recursion ,
 So the compiler doesn't need to stack constantly , So the space complexity is zero  O(1).

LC