当前位置:网站首页>[combinatorics] recursive equation (outline of recursive equation content | definition of recursive equation | example description of recursive equation | Fibonacci Series)
[combinatorics] recursive equation (outline of recursive equation content | definition of recursive equation | example description of recursive equation | Fibonacci Series)
2022-07-03 16:40:00 【Programmer community】
List of articles
- One 、 Recurrence equation Contents summary
- Two 、 Recurrence equation Definition
- 3、 ... and 、 Recurrence equation Example
- Four 、 Fibonacci sequence ( Fibnacci )
One 、 Recurrence equation Contents summary
Recurrence equation Contents summary :
- Recursive equation definition
- Examples of recursive equations
- Constant coefficient linear recurrence equation
- Definition of linear recurrence equation with constant coefficients
- Formula solution
- Application of recurrence equation in counting problem
Two 、 Recurrence equation Definition
Sequence
a
0
,
a
1
,
⋯
,
a
n
,
⋯
a_0 , a_1 , \cdots , a_n , \cdots
a0,a1,⋯,an,⋯ , Remember to do
{
a
n
}
\{a_n\}
{ an} ,
take
a
n
a_n
an And some
a
i
(
i
<
n
)
a_i \ \ ( i < n )
ai (i<n) Connected equations ,
a
i
a_i
ai It can be
1
1
1 individual , It can be multiple ;
take
a
n
a_n
an Use the previous items
a
n
−
1
,
a
n
−
2
,
⋯
a_{n-1} , a_{n-2} , \cdots
an−1,an−2,⋯ Express it ,
be called About sequence
{
a
n
}
\{a_n\}
{ an} Of Recurrence equation ;
The recursive equation consists of : below
3
3
3 One is a set ;
- The sequence
- Recurrence equation
- initial value
Given the recurrence equation , and initial value , Can Uniquely identify a sequence ;
The relationship expressed by recurrence equation : Recurrence equation It only expresses Item is the same as the previous item The relationship between , If Different initial values , The resulting sequence is different ;
The relationship between recurrence equation and sequence : Recursive equations do not represent a sequence , yes Several series Of Common dependencies ;
Recurrence equation , Is to count the result , Expressed as a sequence ,
{
a
n
}
\{a_n\}
{ an} Is the general term formula ;
Sequence example : Such as selecting questions , from
n
n
n Of the elements
r
r
r Elements , If
n
n
n Given , that
r
r
r That's the parameter ,
- When
r
=
0
r = 0
r=0 The number of choices is
a
0
a_0
a0
- When
r
=
1
r = 1
r=1 The number of choices is
a
1
a_1
a1
⋮
\vdots
⋮
- When
r
=
n
r = n
r=n The number of choices is
a
n
a_n
an
The general term of the sequence , Represents some kind of counting result ;
3、 ... and 、 Recurrence equation Example
1 . Factorial calculation sequence :
1
!
,
2
!
,
3
!
,
4
!
,
5
!
,
6
!
,
⋯
1! , 2! , 3! , 4! , 5! , 6! , \cdots
1!,2!,3!,4!,5!,6!,⋯
In sequence The first
1
1
1 Item is
1
1
1 The factorial , The first
2
2
2 Item is
2
2
2 The factorial ,
⋯
\cdots
⋯ , The first
n
n
n Item is
n
n
n The factorial ;
2 . Recurrence equation :
F
(
n
)
=
n
F
(
n
−
1
)
F(n) = nF(n-1)
F(n)=nF(n−1)
Such as : The first
4
4
4 Item value
F
(
4
)
=
5
!
F(4) = 5!
F(4)=5! , It is equal to
4
−
1
=
3
4-1=3
4−1=3 Item value
F
(
4
−
1
)
=
F
(
3
)
=
4
!
F(4-1)=F(3) = 4!
F(4−1)=F(3)=4! multiply
5
5
5 ;
3 . initial value :
F
(
1
)
=
1
F(1) = 1
F(1)=1
according to
F
(
1
)
=
1
F(1) = 1
F(1)=1 You can calculate
F
(
2
)
F(2)
F(2) , according to
F
(
2
)
F(2)
F(2) You can calculate
F
(
3
)
F(3)
F(3) , according to
F
(
3
)
F(3)
F(3) Sure Calculation
F
(
4
)
F(4)
F(4) ,
⋯
\cdots
⋯ , according to
F
(
n
−
1
)
F(n-1)
F(n−1) You can calculate
F
(
n
)
F(n)
F(n) ;
Four 、 Fibonacci sequence ( Fibnacci )
1 . Fibonacci sequence :
1
,
1
,
2
,
3
,
5
,
8
,
13
,
⋯
1 , 1 , 2 , 3 , 5 , 8 , 13 , \cdots
1,1,2,3,5,8,13,⋯
2 . Recurrence equation :
F
(
n
)
=
F
(
n
−
1
)
+
F
(
n
−
2
)
F(n) = F(n-1) + F(n-2)
F(n)=F(n−1)+F(n−2)
describe : The first
n
n
n Item equal to
n
−
1
n-1
n−1 term and The first
n
−
2
n-2
n−2 Sum of items ;
Such as : The first
4
4
4 Item value
F
(
4
)
=
5
F(4) = 5
F(4)=5 , Is equal to
The first
4
−
1
=
3
4-1=3
4−1=3 Item value
F
(
4
−
1
)
=
F
(
3
)
=
3
F(4-1)=F(3) = 3
F(4−1)=F(3)=3
add The first
4
−
2
=
2
4-2=2
4−2=2 Item value
F
(
4
−
2
)
=
F
(
2
)
=
2
F(4-2) = F(2) =2
F(4−2)=F(2)=2 ;
3 . initial value :
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1 , F(1) = 1
F(0)=1,F(1)=1
according to
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1, F(1) = 1
F(0)=1,F(1)=1 You can calculate
F
(
2
)
F(2)
F(2) , according to
F
(
1
)
,
F
(
2
)
F(1),F(2)
F(1),F(2) You can calculate
F
(
3
)
F(3)
F(3) , according to
F
(
2
)
F
(
3
)
F(2)F(3)
F(2)F(3) Sure Calculation
F
(
4
)
F(4)
F(4) ,
⋯
\cdots
⋯ , according to
F
(
n
−
2
)
,
F
(
n
−
1
)
F(n-2) , F(n-1)
F(n−2),F(n−1) You can calculate
F
(
n
)
F(n)
F(n) ;
边栏推荐
- One article takes you to understand machine learning
- 消息队列消息丢失和消息重复发送的处理策略
- Explore Cassandra's decentralized distributed architecture
- Netease UI automation test exploration: airtest+poco
- 0214-27100 a day with little fluctuation
- Register in PHP_ Globals parameter settings
- Shentong express expects an annual loss of nearly 1billion
- Multithread 02 thread join
- Learn from me about the enterprise flutter project: simplified framework demo reference
- 1287. Elements that appear more than 25% in an ordered array
猜你喜欢
Explore Netease's large-scale automated testing solutions see here see here
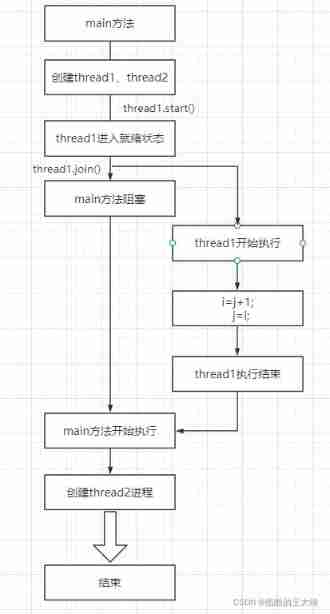
Multithread 02 thread join
word 退格键删除不了选中文本,只能按delete

Myopia: take off or match glasses? These problems must be understood clearly first
一台服务器最大并发 tcp 连接数多少?65535?
Mysql 将逗号隔开的属性字段数据由列转行

Yu Wenwen, Hu Xia and other stars take you to play with the party. Pipi app ignites your summer

什么是质押池,如何进行质押呢?

NLP four paradigms: paradigm 1: fully supervised learning in the era of non neural networks (Feature Engineering); Paradigm 2: fully supervised learning based on neural network (Architecture Engineeri

utfwry. Dat PHP, about ThinkPHP's method of IP location using utfwry address Library
随机推荐
消息队列消息丢失和消息重复发送的处理策略
Eleven requirements for test management post
Unreal_DataTable 实现Id自增与设置RowName
斑馬識別成狗,AI犯錯的原因被斯坦福找到了
Summary of three methods of PHP looping through arrays list (), each (), and while
PyTorch 1.12发布,正式支持苹果M1芯片GPU加速,修复众多Bug
Using optimistic lock and pessimistic lock in MySQL to realize distributed lock
Client does not support authentication protocol requested by server; consider upgrading MySQL client
PHP secondary domain name session sharing scheme
What is the pledge pool and how to pledge?
架构实战营 - 第 6 期 毕业总结
TCP拥塞控制详解 | 3. 设计空间
QT serial port UI design and solution to display Chinese garbled code
Yu Wenwen, Hu Xia and other stars take you to play with the party. Pipi app ignites your summer
Record a jar package conflict resolution process
(补)双指针专题
First knowledge of database
Custom plug-in construction and use of QT plug-in
Page dynamics [2]keyframes
EditText request focus - EditText request focus