当前位置:网站首页>浅谈拉格朗日插值及其应用
浅谈拉格朗日插值及其应用
2022-07-03 16:41:00 【偶耶XJX】
前言
最近在做历年的NOI原题,然后就做到了[NOI2019] 机器人,惊讶地发现我居然没学过拉格朗日插值!
之前的省选题本来有一道拉插的题([省选联考 2022] 填树),但是在 O n e I n D a r k \rm O\red{neInDark} OneInDark 的推荐下用了斯特林反演。其实拉插很简单,而且更适合做像填树、机器人这样的DP优化题目。
简介
粘的别人的
在数值分析中,拉格朗日插值法是以法国18世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。如果对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。上面这样的多项式就称为拉格朗日(插值)多项式。
拉格朗日插值法
众所周知,给出一个 n n n 次多项式的 n + 1 n+1 n+1 个点值可以唯一地求出这个多项式,一个朴素的求法就是列出 n + 1 n+1 n+1 个方程然后使用高斯消元,复杂度 O ( n 3 ) O(n^3) O(n3),往往还伴随精度问题。
而拉格朗日插值法可以在 O ( n 2 ) O(n^2) O(n2) 时间内以足够高的精度求出多项式。
直接上拉格朗日插值公式:
f ( x ) = ∑ i = 0 n y i ∏ j ≠ i x − x j x i − x j f(x)=\sum_{i=0}^ny_i\prod_{j\neq i}\frac{x-x_j}{x_i-x_j} f(x)=i=0∑nyij=i∏xi−xjx−xj这个式子十分巧妙,因为带入后可以发现它刚好能取到所有的点值,并且次数最大为 n n n。
用这个公式直接求多项式虽然也是 O ( n 3 ) O(n^3) O(n3)(还比高消慢),但是是可以优化滴!
我们可以先求出 g ( x ) = ∏ i = 0 n ( x − x i ) g(x)=\prod_{i=0}^n(x-x_i) g(x)=∏i=0n(x−xi),然后枚举 y i y_i yi 时先 O ( n ) O(n) O(n) 计算下面的 ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1,然后由于 g ( x ) g(x) g(x) 在计算的时候没有被掐断,所以单个 ( x − x i ) (x-x_i) (x−xi) 可以整除 g ( x ) g(x) g(x),直接 O ( n ) O(n) O(n) 递推求出 ∏ j ≠ i ( x − x j ) \prod_{j\neq i}(x-x_j) ∏j=i(x−xj) 即可(注意特判 x i = 0 x_i=0 xi=0)。这样总的复杂度就降为了 O ( n 2 ) O(n^2) O(n2)。
求单个点值
这里求单个点值的意思是给出 k ∉ { x i ∣ 0 ≤ i ≤ n } k\notin \{x_i|0\le i\le n\} k∈/{ xi∣0≤i≤n},我们需要求 f ( k ) f(k) f(k)。
我们显然可以直接求出 f ( x ) f(x) f(x) 然后带入求解,但是当我们的目的仅仅是求出 f ( k ) f(k) f(k) 时,这么做就显得麻烦且低效。
我们不妨直接带入拉格朗日插值公式:
f ( k ) = ∑ i = 0 n y i ∏ j ≠ i k − x j x i − x j f(k)=\sum_{i=0}^ny_i\prod_{j\neq i}\frac{k-x_j}{x_i-x_j} f(k)=i=0∑nyij=i∏xi−xjk−xj由于不再是求多项式,所以我们可以在 O ( n ) O(n) O(n) 时间内求出所有的 ∏ j ≠ i ( k − x j ) \prod_{j\neq i}(k-x_j) ∏j=i(k−xj),然后每次枚举 y i y_i yi 时就只用求 ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1 了。虽然还是 O ( n 2 ) O(n^2) O(n2),但是减小了常数且更简单。
O(n)求单个点值
还是只要求求出 f ( k ) f(k) f(k)。
在多数应用到拉插的题目中,这 n + 1 n+1 n+1 个点值是满足下标连续,或者等间距的,即 x 1 − x 0 = x 2 − x 1 = . . . = x n − x n − 1 x_1-x_0=x_2-x_1=...=x_n-x_{n-1} x1−x0=x2−x1=...=xn−xn−1。
此时我们可以做些预处理(比如当间距等于 1 的时候,你需要预处理阶乘的逆元),然后就可以单次 O ( 1 ) O(1) O(1) 求出 ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1。(需要特别注意符号问题)
应用
有一个经典问题:计算 ∑ i = 1 n i k \sum_{i=1}^ni^k ∑i=1nik。这个问题显然可以用斯特林反演 O ( k log k ∼ k 2 ) O(k\log k\sim k^2) O(klogk∼k2) 解决。
众所周知这个东西是一个关于 n n n 的 k + 1 k+1 k+1 次多项式,所以我们可以先 O ( k ) O(k) O(k)(忽略快速幂,你也可以用线性筛)求出前 k + 2 k+2 k+2 个点值,然后用上面的方法 O ( k ) O(k) O(k) 拉插求出 n n n 处的答案,这样总复杂度只有 O ( k ) O(k) O(k)。
更实用的场景是在一些DP题中,比如你需要求 m m m 个DP值来转移,但是你发现这 m m m 个点值的函数是一个次数较小的 n n n 次多项式,那么就可以只求前 n + 1 n+1 n+1 个DP值,剩下的拉插即可。
一般要看出这是个多项式需要归纳证明,但是我不会
边栏推荐
- Two sides of the evening: tell me about the bloom filter and cuckoo filter? Application scenario? I'm confused..
- Is it safe to open a stock account by mobile registration? Does it need money to open an account
- [combinatorics] polynomial theorem (polynomial coefficients | full arrangement of multiple sets | number of schemes corresponding to the ball sub model | polynomial coefficient correlation identity)
- Everyone in remote office works together to realize cooperative editing of materials and development of documents | community essay solicitation
- Using optimistic lock and pessimistic lock in MySQL to realize distributed lock
- Why does the std:: string operation perform poorly- Why do std::string operations perform poorly?
- [Jianzhi offer] 64 Find 1+2+... +n
- 关于视觉SLAM的最先进技术的调查-A survey of state-of-the-art on visual SLAM
- IL Runtime
- Multithread 02 thread join
猜你喜欢

Deep understanding of grouping sets statements in SQL
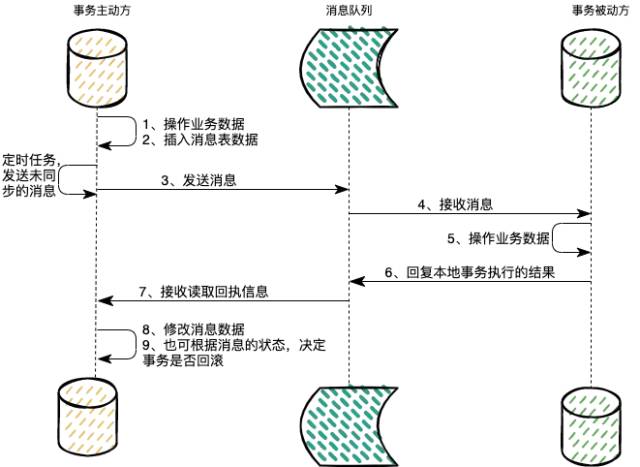
消息队列消息丢失和消息重复发送的处理策略

What material is 12cr1movr? Chemical property analysis of pressure vessel steel plate 12cr1movr

What is the pledge pool and how to pledge?
QT serial port UI design and solution to display Chinese garbled code
智慧之道(知行合一)

Add color to the interface automation test framework and realize the enterprise wechat test report

Daily code 300 lines learning notes day 10
![[solved] access denied for user 'root' @ 'localhost' (using password: yes)](/img/71/1ff8ed1d773da99054310f96dca3f8.jpg)
[solved] access denied for user 'root' @ 'localhost' (using password: yes)

NFT new opportunity, multimedia NFT aggregation platform okaleido will be launched soon
随机推荐
香港理工大学|数据高效的强化学习和网络流量动态的自适应最优周界控制
TCP congestion control details | 3 design space
What material is sa537cl2 equivalent to in China? Sa537cl2 corresponding material
There are several APIs of airtest and poco that are easy to use wrong in "super". See if you have encountered them
【剑指 Offer】58 - II. 左旋转字符串
Page dynamics [2]keyframes
Preventing/catching “IllegalArgumentException: parameter must be a descendant of this view” error
利用MySQL中的乐观锁和悲观锁实现分布式锁
CC2530 common registers
Register in PHP_ Globals parameter settings
Everyone in remote office works together to realize cooperative editing of materials and development of documents | community essay solicitation
PyTorch 1.12发布,正式支持苹果M1芯片GPU加速,修复众多Bug
Mysql 将逗号隔开的属性字段数据由列转行
What material is sa537cl1? Sa537cl1 corresponds to the national standard material
8 tips for effective performance evaluation
Golang 装饰器模式以及在NSQ中的使用
深入理解 SQL 中的 Grouping Sets 语句
nifi从入门到实战(保姆级教程)——flow
Difference between JSON and bson
线程池执行定时任务
