[combinatorics] non descending path problem (number of non descending paths with constraints)

One 、 The number of non descending paths of the constraint

---

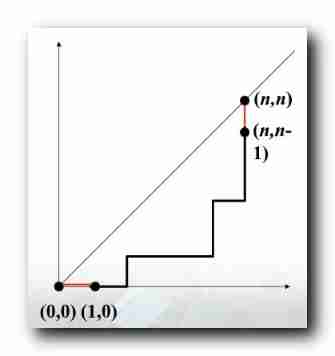
from

(

0

,

0

)

(0,0)

(0,0) To

(

n

,

n

)

(n,n)

(n,n) Except endpoint , The number of non descending paths that do not touch the diagonal ?

At this time, the basic formula cannot be used for processing , You must use the idea of combining correspondence ;

In the example above , from

(

0

,

0

)

(0,0)

(0,0) Set out to

(

n

,

n

)

(n,n)

(n,n) , There are only two endpoints

(

0

,

0

)

(0,0)

(0,0) and

(

n

,

n

)

(n,n)

(n,n) Touching the diagonal , Every step in the middle does not touch the diagonal ;

1 . Calculation principle , First calculate the non descending path below the diagonal : Here, only the number of non descending paths below the diagonal is counted , because The non descending path above and below the diagonal is symmetric , So here First calculate the non descending path below the diagonal ;

The non descending path below the diagonal multiply

2

2

2 , That's all Not touching the diagonal Number of non descending paths ;

2 . Starting point analysis : from

(

0

,

0

)

(0,0)

(0,0) After departure , The first

1

1

1 Step must go to the right , Go to the

(

1

,

0

)

(1, 0)

(1,0) spot , If you go up, you can't come down anymore ( Otherwise, it will touch the diagonal ) , At this time, it is not the non descending path below the diagonal ;

3 . End point analysis :

arrive

(

n

,

n

)

(n,n)

(n,n) spot , There are only two cases :

• Above the diagonal : One case is from the left $(n-1,n)$
• Below the diagonal : One situation is from the bottom $(n,n-1)$

At present, only The number of non descending paths below the diagonal , arrive

(

n

,

n

)

(n,n)

(n,n) The previous step , Must be from

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Position go to

(

n

,

n

)

(n,n)

(n,n) Of ;

4 . Corresponding relation

Above You must leave after the starting point

(

1

,

0

)

(1, 0)

(1,0) spot , You must go before the end

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) spot ,

therefore Below the diagonal from

(

0

,

0

)

(0,0)

(0,0) To

(

n

,

n

)

(n,n)

(n,n) Except endpoint , The number of non descending paths that do not touch the diagonal

Equivalent to

from

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal

5 . Calculation

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal

Let's talk about “ from

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal ” How to count ;

Think in reverse , Statistics from

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Between , The non descending path that touches the diagonal , The rest is the path that does not touch the diagonal ;

The total of the above two is

C

(

2

n

−

2

,

n

−

1

)

C(2n-2 , n-1)

C(2n−2,n−1) individual ;

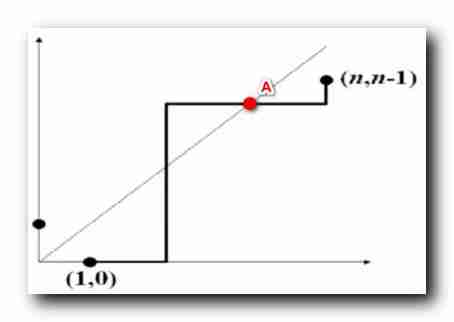
Above, One “ from

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) , The non descending path that touches the diagonal ” ,

In the picture Red dot

A

A

A Is the position where the non descending path finally contacts the diagonal , The front may touch the diagonal many times ;

take

(

1

,

0

)

(1, 0)

(1,0) spot And

A

A

A spot Blue line segment between , Make a symmetrical image about the diagonal , obtain Red line ,

In the picture above Blue line segment The starting point is

(

1

,

0

)

(1,0)

(1,0), So the corresponding The starting point of the red line segment must be

(

0

,

1

)

(0,1)

(0,1) ;

Every one from

(

1

,

0

)

(1,0)

(1,0) Start to

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) The non descending path of the contact diagonal , There are blue line segments , Can use symmetrical method , Get one from

(

0

,

1

)

(0,1)

(0,1) arrive

A

A

A The red line segment of the dot ;

Here we get a combinatorial correspondence :

Each from

(

0

,

1

)

(0,1)

(0,1) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Of Non descending path ( the Red line segment And remainder Black line segment Paths that can be spliced )

Can and

from

(

1

,

0

)

(1,0)

(1,0) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Contact diagonal Non descending path

One-to-one correspondence ;

So if required " from

(

1

,

0

)

(1,0)

(1,0) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Contact diagonal Number of non descending paths " , You can ask for “ from

(

0

,

1

)

(0,1)

(0,1) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Of Number of non descending paths ” ;

“ from

(

0

,

1

)

(0,1)

(0,1) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Of Number of non descending paths ” You can use formulas to calculate , The result is

C

(

2

n

−

2

,

n

)

C(2n - 2 , n)

C(2n−2,n) ,

Corresponding " from

(

1

,

0

)

(1,0)

(1,0) set out , To

(

n

,

n

−

1

)

(n, n-1)

(n,n−1) Contact diagonal Number of non descending paths " , The result is

C

(

2

n

−

2

,

n

)

C(2n - 2 , n)

C(2n−2,n) ;

6 . Calculation

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) The number of all non descending paths

Calculate according to the formula , The result is :

C

(

2

n

−

2

,

n

−

1

)

C(2n - 2 , n-1)

C(2n−2,n−1)

7 . Calculation

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal

"

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal " Namely

"

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) The number of all non descending paths " subtract "

(

1

,

0

)

(1, 0)

(1,0) To

(

n

,

n

−

1

)

(n,n-1)

(n,n−1) Except endpoint , The number of non descending paths that do not touch the diagonal " ;

    

C

(

2

n

−

2

,

n

−

1

)

−

C

(

2

n

−

2

,

n

)

\ \ \ \ C(2n - 2 , n-1) - C(2n - 2 , n)

    C(2n−2,n−1)−C(2n−2,n)

=

(

2

n

−

2

n

−

1

)

−

(

2

n

−

2

n

)

=\dbinom{2n - 2}{n-1} - \dbinom{2n - 2}{n}

=(n−12n−2​)−(n2n−2​)

8 . Calculation from

(

0

,

0

)

(0,0)

(0,0) To

(

n

,

n

)

(n,n)

(n,n) Except endpoint , The number of non descending paths that do not touch the diagonal

above

(

2

n

−

2

n

−

1

)

−

(

2

n

−

2

n

)

\dbinom{2n - 2}{n-1} - \dbinom{2n - 2}{n}

(n−12n−2​)−(n2n−2​) It only calculates the number of non descending paths below the diagonal ,

from

(

0

,

0

)

(0,0)

(0,0) set out , To

(

n

,

n

)

(n,n)

(n,n) The number of non descending paths that do not touch the diagonal , Multiplied by

2

2

2 , You get the final result of this topic ;

from

(

0

,

0

)

(0,0)

(0,0) To

(

n

,

n

)

(n,n)

(n,n) Except endpoint , The number of non descending paths that do not touch the diagonal

The end result is :

2

[

(

2

n

−

2

n

−

1

)

−

(

2

n

−

2

n

)

]

2[\dbinom{2n - 2}{n-1} - \dbinom{2n - 2}{n}]

2[(n−12n−2​)−(n2n−2​)]