当前位置:网站首页>[combinatorics] recursive equation (example of solving recursive equation without multiple roots | complete process of solving recursive equation without multiple roots)
[combinatorics] recursive equation (example of solving recursive equation without multiple roots | complete process of solving recursive equation without multiple roots)
2022-07-03 17:06:00 【Programmer community】
List of articles
- One 、 Fibonacci sequence solution
- Two 、 Complete process of solving recursive equations without multiple roots
One 、 Fibonacci sequence solution
1 . Fibonacci sequence example :
( 1 ) Fibonacci sequence :
1
,
1
,
2
,
3
,
5
,
8
,
13
,
⋯
1 , 1 , 2 , 3 , 5 , 8 , 13 , \cdots
1,1,2,3,5,8,13,⋯
( 2 ) Recurrence equation :
F
(
n
)
=
F
(
n
−
1
)
+
F
(
n
−
2
)
F(n) = F(n-1) + F(n-2)
F(n)=F(n−1)+F(n−2)
describe : The first
n
n
n Item equal to
n
−
1
n-1
n−1 term and The first
n
−
2
n-2
n−2 Sum of items ;
Such as : The first
4
4
4 Item value
F
(
4
)
=
5
F(4) = 5
F(4)=5 , Is equal to
The first
4
−
1
=
3
4-1=3
4−1=3 Item value
F
(
4
−
1
)
=
F
(
3
)
=
3
F(4-1)=F(3) = 3
F(4−1)=F(3)=3
add The first
4
−
2
=
2
4-2=2
4−2=2 Item value
F
(
4
−
2
)
=
F
(
2
)
=
2
F(4-2) = F(2) =2
F(4−2)=F(2)=2 ;
( 3 ) initial value :
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1 , F(1) = 1
F(0)=1,F(1)=1
according to
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1, F(1) = 1
F(0)=1,F(1)=1 You can calculate
F
(
2
)
F(2)
F(2) , according to
F
(
1
)
,
F
(
2
)
F(1),F(2)
F(1),F(2) You can calculate
F
(
3
)
F(3)
F(3) , according to
F
(
2
)
F
(
3
)
F(2)F(3)
F(2)F(3) Sure Calculation
F
(
4
)
F(4)
F(4) ,
⋯
\cdots
⋯ , according to
F
(
n
−
2
)
,
F
(
n
−
1
)
F(n-2) , F(n-1)
F(n−2),F(n−1) You can calculate
F
(
n
)
F(n)
F(n) ;
2 . Write the characteristic equation of Fibonacci sequence and solve the characteristic root :
Recurrence equation :
F
(
n
)
=
F
(
n
−
1
)
+
F
(
n
−
2
)
F(n) = F(n-1) + F(n-2)
F(n)=F(n−1)+F(n−2)
( 1 ) The standard form of recurrence equation :
F
(
n
)
−
F
(
n
−
1
)
−
F
(
n
−
2
)
=
0
F(n) - F(n-1) - F(n-2) = 0
F(n)−F(n−1)−F(n−2)=0
( 2 ) Recursive equation writing :
① First determine the number of terms of the characteristic equation : The same number of terms as the recursive equation ,
3
3
3 term ;
② In determining the characteristic equation
x
x
x Power of power : from
3
−
1
=
2
3-1=2
3−1=2 To
0
0
0 ;
③ Write a recurrence equation without coefficients :
x
2
+
x
1
+
x
0
=
0
x^2 + x^1 + x^0 = 0
x2+x1+x0=0
④ Filling factor : Then the characteristic equation without coefficients
x
2
+
x
1
+
x
0
=
0
x^2 + x^1 + x^0 = 0
x2+x1+x0=0 And
F
(
n
)
−
F
(
n
−
1
)
−
F
(
n
−
2
)
=
0
F(n) - F(n-1) - F(n-2) = 0
F(n)−F(n−1)−F(n−2)=0 The coefficients of corresponding bits are filled into the characteristic equation :
x
2
x^2
x2 The coefficient before Corresponding
F
(
n
)
F(n)
F(n) Coefficient before item
1
1
1 ;
x
1
x^1
x1 The coefficient before Corresponding
F
(
n
−
1
)
F(n-1)
F(n−1) Coefficient before item
−
1
-1
−1 ;
x
0
x^0
x0 The coefficient before Corresponding
F
(
n
−
2
)
F(n-2)
F(n−2) Coefficient before item
−
1
-1
−1 ;
Then the final The characteristic equation is
1
x
2
+
(
−
1
)
x
1
+
(
−
1
)
x
0
=
0
1 x^2 + (-1)x^1 + (-1)x^0 = 0
1x2+(−1)x1+(−1)x0=0 , It is reduced to :
x
2
−
x
−
1
=
0
x^2 - x - 1 = 0
x2−x−1=0
The characteristic root of the characteristic equation is : The solution of the above equation is the characteristic root , Generally, it is a quadratic equation with one variable ;
x
=
1
±
5
2
x = \cfrac{1 \pm \sqrt{5}}{2}
x=21±5
Reference resources : Univariate quadratic equation form
a
x
2
+
b
x
+
c
=
0
ax^2 + bx + c = 0
ax2+bx+c=0
The solution is :x
=
−
b
±
b
2
−
4
a
c
2
a
x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x=2a−b±b2−4ac
3 . Write the general solution of Fibonacci sequence :
The characteristic root of Fibonacci series recurrence equation is :
1
±
5
2
\cfrac{1 \pm \sqrt{5}}{2}
21±5 ;
q
1
=
1
+
5
2
q_1 = \cfrac{1 + \sqrt{5}}{2}
q1=21+5 ,
q
2
=
1
−
5
2
q_2 =\cfrac{1 - \sqrt{5}}{2}
q2=21−5
The general solution is in the form of
F
(
n
)
=
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
F(n) = c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
F(n)=c1q1n+c2q2n+⋯+ckqkn
Set feature root
q
1
,
q
2
q_1 , q_2
q1,q2 After substituting the above general solution form, it becomes :
F
(
n
)
=
c
1
(
1
+
5
2
)
n
+
c
2
(
1
−
5
2
)
n
F(n) = c_1 ( \cfrac{1 + \sqrt{5}}{2} ) ^n + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) ^n
F(n)=c1(21+5)n+c2(21−5)n
4 . Substitute the initial value of the recurrence equation into general solution , Solve the constants in the general solution :
Fibonacci sequence Initial value of recurrence equation :
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1 , F(1) = 1
F(0)=1,F(1)=1
Substitute the above initial value
F
(
0
)
=
1
,
F
(
1
)
=
1
F(0) = 1 , F(1) = 1
F(0)=1,F(1)=1 To General solution of recurrence equation
F
(
n
)
=
c
1
(
1
+
5
2
)
n
+
c
2
(
1
−
5
2
)
n
F(n) = c_1 ( \cfrac{1 + \sqrt{5}}{2} ) ^n + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) ^n
F(n)=c1(21+5)n+c2(21−5)n in , The following equations are obtained :
{
c
1
(
1
+
5
2
)
0
+
c
2
(
1
−
5
2
)
0
=
F
(
0
)
=
1
c
1
(
1
+
5
2
)
1
+
c
2
(
1
−
5
2
)
1
=
F
(
1
)
=
1
\begin{cases} c_1 ( \cfrac{1 + \sqrt{5}}{2} ) ^0 + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) ^0 = F(0) = 1 \\\\ c_1 ( \cfrac{1 + \sqrt{5}}{2} ) ^1 + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) ^1 = F(1) = 1 \end{cases}
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧c1(21+5)0+c2(21−5)0=F(0)=1c1(21+5)1+c2(21−5)1=F(1)=1
After simplification, we get :
{
c
1
+
c
2
=
1
c
1
(
1
+
5
2
)
+
c
2
(
1
−
5
2
)
=
1
\begin{cases} c_1 + c_2 = 1 \\\\ c_1 ( \cfrac{1 + \sqrt{5}}{2} ) + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) = 1 \end{cases}
⎩⎪⎪⎨⎪⎪⎧c1+c2=1c1(21+5)+c2(21−5)=1
Solve the above equations :
c
1
=
1
5
1
+
5
2
,
c
2
=
−
1
5
1
−
5
2
c_1 =\cfrac{1}{\sqrt{5}} \cfrac{1 + \sqrt{5}}{2}, \ \ c_2 =-\cfrac{1}{\sqrt{5}} \cfrac{1 - \sqrt{5}}{2}
c1=5121+5, c2=−5121−5
Will constant
c
1
=
1
5
1
+
5
2
,
c
2
=
−
1
5
1
−
5
2
c_1 =\cfrac{1}{\sqrt{5}} \cfrac{1 + \sqrt{5}}{2}, \ \ c_2 =-\cfrac{1}{\sqrt{5}} \cfrac{1 - \sqrt{5}}{2}
c1=5121+5, c2=−5121−5 Substitute into the general solution
F
(
n
)
=
c
1
(
1
+
5
2
)
n
+
c
2
(
1
−
5
2
)
n
F(n) = c_1 ( \cfrac{1 + \sqrt{5}}{2} ) ^n + c_2 ( \cfrac{1 - \sqrt{5}}{2} ) ^n
F(n)=c1(21+5)n+c2(21−5)n in , You can get a general solution :
F
(
n
)
=
1
5
1
+
5
2
(
1
+
5
2
)
n
−
1
5
1
−
5
2
(
1
−
5
2
)
n
F(n) = \cfrac{1}{\sqrt{5}} \cfrac{1 + \sqrt{5}}{2} ( \cfrac{1 + \sqrt{5}}{2} ) ^n - \cfrac{1}{\sqrt{5}} \cfrac{1 - \sqrt{5}}{2} ( \cfrac{1 - \sqrt{5}}{2} ) ^n
F(n)=5121+5(21+5)n−5121−5(21−5)n
It is reduced to :
F
(
n
)
=
1
5
(
1
+
5
2
)
n
+
1
−
1
5
(
1
−
5
2
)
n
+
1
F(n) = \cfrac{1}{\sqrt{5}}( \cfrac{1 + \sqrt{5}}{2} ) ^{n+1} - \cfrac{1}{\sqrt{5}} ( \cfrac{1 - \sqrt{5}}{2} ) ^{n+1}
F(n)=51(21+5)n+1−51(21−5)n+1
Two 、 Complete process of solving recursive equations without multiple roots
Complete process of solving recursive equations without multiple roots :
- 1 . Write the characteristic equation :
- ( 1 ) The standard form of recurrence equation : Write the recurrence equation Standard form , All items are to the left of the equal sign , On the right is
0
0
0 ;
- ( 2 ) Number of terms of characteristic equation : determine Number of terms of characteristic equation , And The recurrence equation has the same number of terms ;
- ( 3 ) The characteristic equation is sub idempotent : The highest power is Number of terms of characteristic equation
−
1
-1
0
0
0 ;
−1 , Lowest power
- ( 4 ) Write There is no coefficient The characteristic equation of ;
- ( 5 ) The coefficients of the recursive equation will be deduced bit by bit Copy Into the characteristic equation ;
- ( 1 ) The standard form of recurrence equation : Write the recurrence equation Standard form , All items are to the left of the equal sign , On the right is
- 2 . Solution characteristic root : take The eigenvalue of the characteristic equation is solved ,
x
=
−
b
±
b
2
−
4
a
c
2
a
x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x=2a−b±b2−4ac
- 3 . Construct the general solution of recurrence equation : structure
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
c1q1n+c2q2n+⋯+ckqkn Linear combination of forms , The linear combination is the solution of the recursive equation ;
- 4 . Find the constant in the general solution : Substitute the initial value of the recursive equation into the general solution , obtain
k
k
k individual
k
k
k Finite element equations , By solving the equations , Get the constant in the general solution ;
- ( 1 ) The constant is substituted into the general solution : Get the final solution of the recursive equation ;
Recurrence equation -> Characteristic equation -> Characteristic root -> general solution -> Substitute the initial value to find the general solution constant
边栏推荐
- Solution to long waiting time of SSH connection to remote host
- Rsync远程同步
- Apache service suspended asynchronous acceptex failed
- visual studio “通常每个套接字地址(协议/网络地址/端口)只允许使用一次“
- How SVN views modified file records
- 网络硬盘NFS的安装与配置
- One brush 145 force deduction hot question-2 sum of two numbers (m)
- [combinatorics] recursive equation (characteristic equation and characteristic root | example of characteristic equation | root formula of monadic quadratic equation)
- 數據分析必備的能力
- What material is sa537cl2 equivalent to in China? Sa537cl2 corresponding material
猜你喜欢

CC2530 common registers for ADC single channel conversion
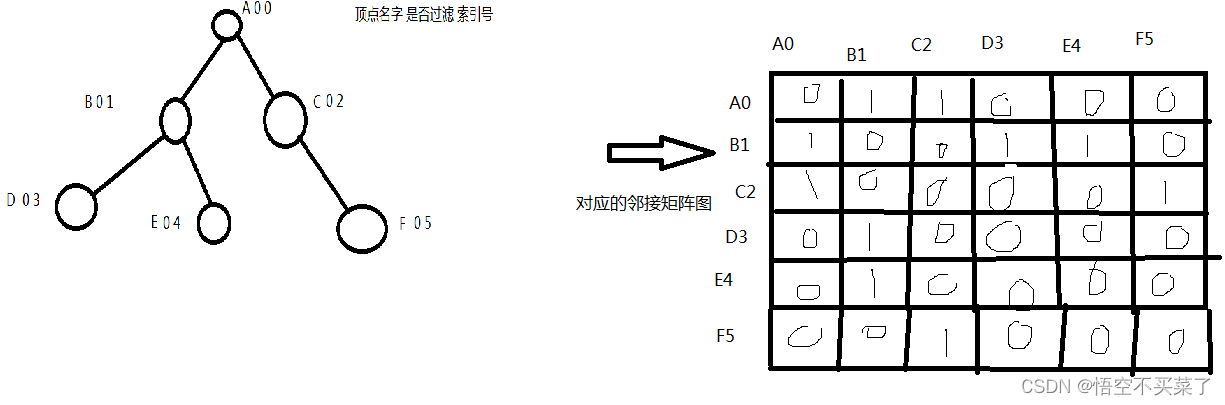
Depth first search of graph
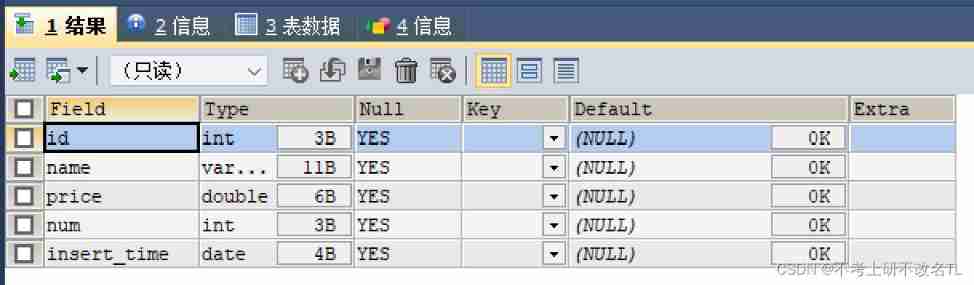
Mysql database DDL and DML

What is the pledge pool and how to pledge?
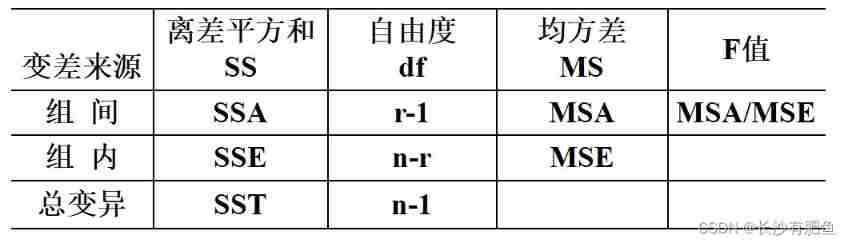
Analysis of variance summary
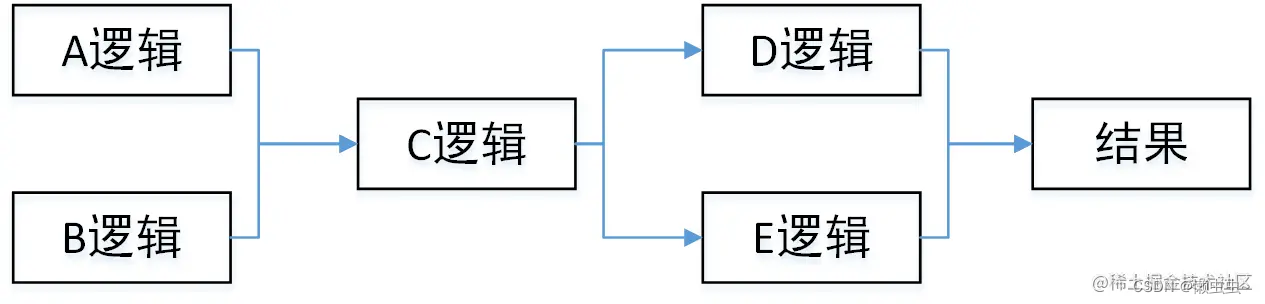
聊聊接口优化的几个方法
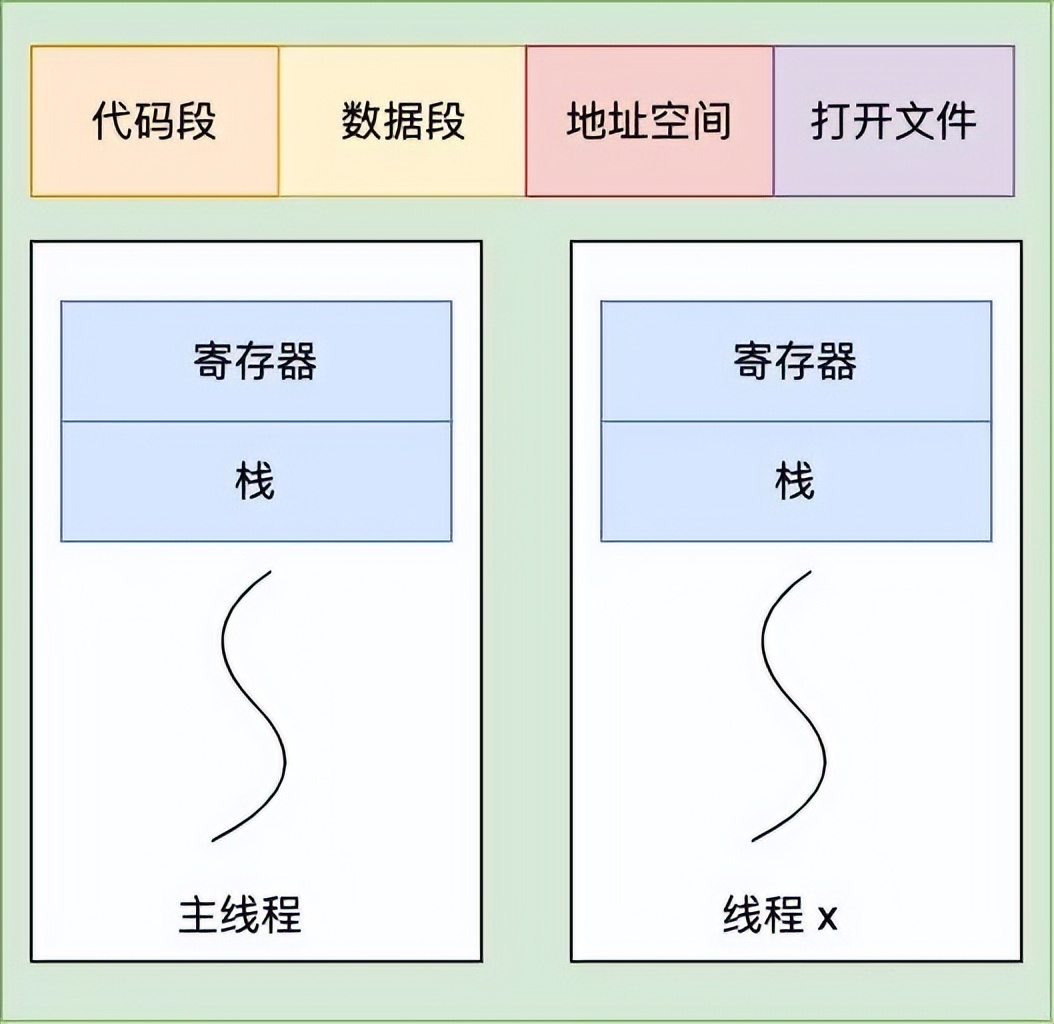
美团一面:为什么线程崩溃崩溃不会导致 JVM 崩溃
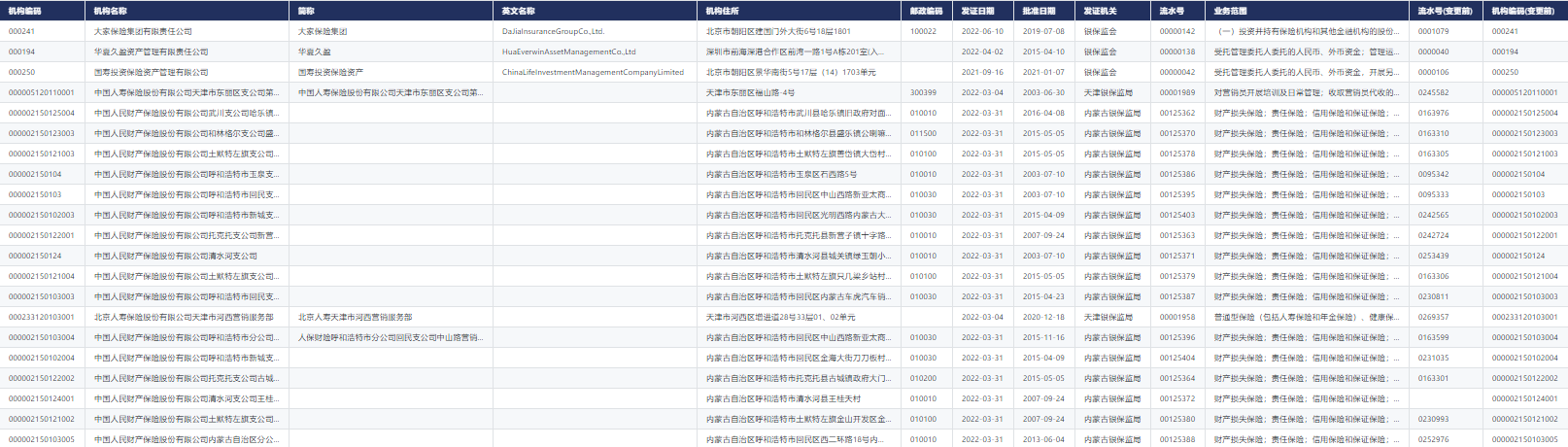
New library online | cnopendata complete data of Chinese insurance institution outlets
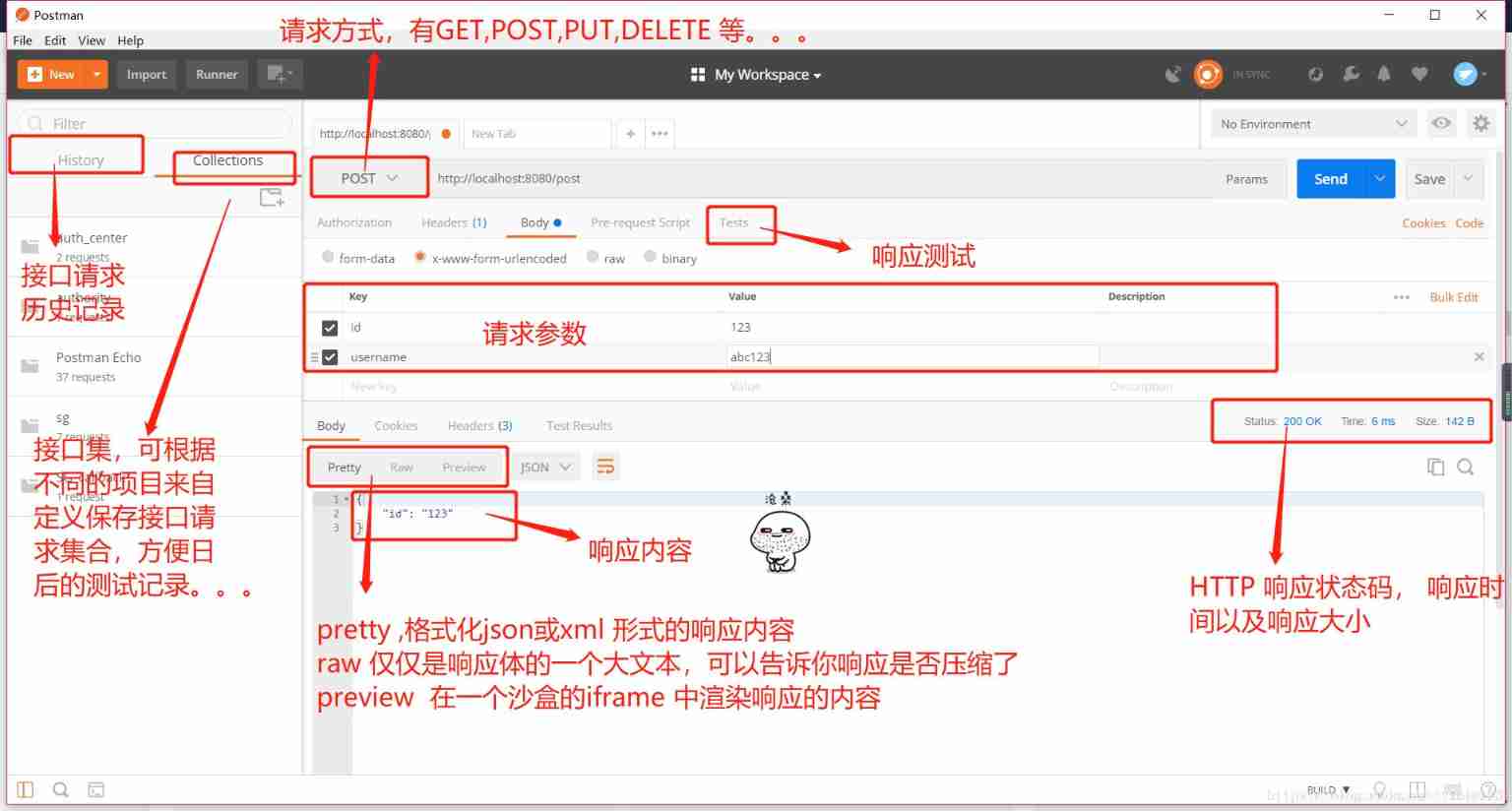
The most complete postman interface test tutorial in the whole network, API interface test

静态程序分析(一)—— 大纲思维导图与内容介绍
随机推荐
LeetCode 1657. Determine whether the two strings are close
[combinatorics] recursive equation (outline of recursive equation content | definition of recursive equation | example description of recursive equation | Fibonacci Series)
[combinatorics] polynomial theorem (polynomial theorem | polynomial theorem proof | polynomial theorem inference 1 item number is the number of non negative integer solutions | polynomial theorem infe
27. 输入3个整数,按从大到小的次序输出。要求用指针方法实现。
Pools de Threads: les composants les plus courants et les plus sujets aux erreurs du Code d'affaires
汇编实例解析--实模式下屏幕显示
Capacités nécessaires à l'analyse des données
Shentong express expects an annual loss of nearly 1billion
PHP converts a one-dimensional array into a two-dimensional array
CC2530 common registers for port interrupts
[2. Basics of Delphi grammar] 2 Object Pascal data type
Mysql database DDL and DML
CC2530 common registers for ADC single channel conversion
Hands on in-depth learning notes (XIV) 3.7 Simple implementation of softmax regression
Kotlin learning quick start (7) -- wonderful use of expansion
[try to hack] active detection and concealment technology
What kind of material is 14Cr1MoR? Analysis of chemical composition and mechanical properties of 14Cr1MoR
HP 阵列卡排障一例
关于学习Qt编程的好书精品推荐
What is the difference between 14Cr1MoR container plate and 14Cr1MoR (H)? Chemical composition and performance analysis of 14Cr1MoR