当前位置:网站首页>[combinatorics] recursive equation (example 1 of recursive equation | list recursive equation)
[combinatorics] recursive equation (example 1 of recursive equation | list recursive equation)
2022-07-03 16:41:00 【Programmer community】
List of articles
- One 、 Examples of recursive equations 1
- Two 、 Summary of recursive equation examples
One 、 Examples of recursive equations 1
The coding system uses
8
8
8 Hexadecimal Numbers , Code the information ,
8
8
8 Hexadecimal digits can only be taken
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7 ,
Only when a code contains Even number
7
7
7 when , This code is valid ,
seek
n
n
n The number of valid codes in the coding of bits ?
analysis :
n
n
n Bit length encoding , Sure from
n
−
1
n-1
n−1 Bit length encoding , Followed by a
8
8
8 Hexadecimal Numbers constitute ;
For each
n
−
1
n-1
n−1 Bit length encoding , Add a digit after it , Make the final coding Satisfy Requirements for effective coding , It contains an even number
7
7
7 , You can get an effective
n
n
n Bit length encoding ;
1 . set up
n
n
n The number of effective codes of bit length is
a
n
a_n
an individual ;
Then there are
n
−
1
n-1
n−1 The number of effective codes of bit length is
a
n
−
1
a_{n-1}
an−1 individual ;
Now consider
n
n
n Bit length encoding And
n
−
1
n-1
n−1 The correlation between bit length codes ;
( 1 ) Even number
7
7
7 : Suppose there is already one
n
−
1
n-1
n−1 Bit long
8
8
8 Hexadecimal encoding string , It happens to contain an even number
7
7
7 , That is, the code has met the requirements of effective coding , Add a digit :
- Figures that cannot be added : Cannot add
7
7
7 , added
7
7
7 after , Will become An odd number
7
7
7 , Become invalid code ;
- Numbers that can be added : Can only add
0
,
1
,
2
,
3
,
4
,
5
,
6
0,1,2,3,4,5,6
0,1,2,3,4,5,6 Numbers , Here you are
7
7
7 Ways of planting ;
By a
n
−
1
n-1
n−1 Bit long , Code that meets the requirements , Yes
7
7
7 There are ways to generate one
n
n
n Bit length encoding ;
( 2 ) An odd number
7
7
7 : Suppose there is already one
n
−
1
n-1
n−1 Bit long
8
8
8 Hexadecimal encoding string , It happens to contain an odd number
7
7
7 , That is, the code does not meet the requirements of effective coding , Add a digit :
- Figures that cannot be added : Cannot add
0
,
1
,
2
,
3
,
4
,
5
,
6
0,1,2,3,4,5,6
0,1,2,3,4,5,6 Numbers , After adding , The final result is still an odd number
7
7
7 , Does not meet the requirements of effective coding ;
- Numbers that can be added : Can only add
7
7
7 , added
7
7
7 after , Will become Even number
7
7
7 , Become a valid code ;
By a
n
−
1
n-1
n−1 Bit long , Codes that do not meet the requirements , Yes
1
1
1 There are ways to generate one
n
n
n Bit length encoding ;
3 . Total number
8
n
−
1
8^{n-1}
8n−1 :
n
−
1
n-1
n−1 The total number of bit length encodings is
8
n
−
1
8^{n-1}
8n−1 individual , Every position has
8
8
8 Two possible options , Yes
n
−
1
n-1
n−1 A place ;
It can also be expressed as :
n
−
1
n-1
n−1 Bits long include , An odd number
7
7
7 , Even number
7
7
7 , The total number of codes is
8
n
−
1
8^{n-1}
8n−1
If there is no
7
7
7 , yes
0
0
0 individual
7
7
7 , Count even numbers
7
7
7 ;
4 .
n
−
1
n-1
n−1 The effective number of bit codes
a
n
−
1
a_{n-1}
an−1 :
n
−
1
n-1
n−1 In a , Even number
7
7
7 The number of , Is the number of effective codes , That is, the above hypothetical
“ set up
n
n
n The number of effective codes of bit length is
a
n
a_n
an individual ” , Then there are
"
n
−
1
n-1
n−1 The number of effective codes of bit length is
a
n
−
1
a_{n-1}
an−1 individual "
5 .
n
−
1
n-1
n−1 Invalid number of bit codes
8
n
−
1
−
a
n
−
1
8^{n-1} - a_{n-1}
8n−1−an−1 :
n
−
1
n-1
n−1 Bits long include An odd number
7
7
7 , Even number
7
7
7 Of The total number of codes is
8
n
−
1
8^{n-1}
8n−1
n
−
1
n-1
n−1 In a , Even number
7
7
7 The number of , Namely Number of valid codes , That is, the above hypothetical
a
n
−
1
a_{n-1}
an−1
be
n
−
1
n-1
n−1 In a , An odd number
7
7
7 The number of , Is the number of invalid codes , The aforementioned Subtract the number of effective codes from the total number , The result is :
8
n
−
1
−
a
n
−
1
8^{n-1} - a_{n-1}
8n−1−an−1
6 . Analysis section
n
n
n Item and
n
−
1
n-1
n−1 The relationship between items , namely
n
n
n Number of bit effective codes And
n
−
1
n-1
n−1 Number of bit effective codes :
The number of adding methods corresponding to the number of effective codes :
n
−
1
n-1
n−1 The effective number of bit codes
a
n
−
1
a_{n-1}
an−1 , Contains an even number of
7
7
7 , Each valid code , Add one digit , form
n
n
n Bit valid encoding , Yes
7
7
7 Corresponding addition methods , Add
0
,
1
,
2
,
3
,
4
,
5
,
6
0,1,2,3,4,5,6
0,1,2,3,4,5,6 Numbers , Seven ways ; The number of methods is
7
a
n
−
1
7a_{n-1}
7an−1
The number of adding methods corresponding to the number of invalid codes :
n
−
1
n-1
n−1 Invalid number of bit codes
8
n
−
1
−
a
n
−
1
8^{n-1} - a_{n-1}
8n−1−an−1 , There are also odd numbers
7
7
7 , Each invalid code , Only one number can be added
7
7
7 , form
n
n
n Bit valid encoding , There is only one way ; The number of methods is
8
n
−
1
−
a
n
−
1
8^{n-1} - a_{n-1}
8n−1−an−1
So here we can write
n
n
n The effective number of bit codes
a
n
a_n
an And
n
−
1
n-1
n−1 Effective number of bit codes
a
n
−
1
a_{n-1}
an−1 The relationship between :
a
n
a_n
an
=
=
=
7
a
n
−
1
7a_{n-1}
7an−1
+
+
+
8
n
−
1
−
a
n
−
1
8^{n-1} - a_{n-1}
8n−1−an−1
After simplification, we get :
a
n
a_n
an
=
=
=
6
a
n
−
1
6a_{n-1}
6an−1
+
+
+
8
n
−
1
8^{n-1}
8n−1
7 . Initial value discussion
If only
1
1
1 Bit code , It can't be
7
7
7 , This will contain an odd number (
1
1
1 individual )
7
7
7 , Is an invalid code ;
Can only be
0
,
1
,
2
,
3
,
4
,
5
,
6
0,1,2,3,4,5,6
0,1,2,3,4,5,6 this
7
7
7 Kind of , So there is
1
1
1 Bit encoding , The number of effective codes is
7
7
7 individual ,
produce Initial value of recurrence equation
a
1
=
7
a_1 = 7
a1=7
8 . The resulting recursive equation :
Recurrence equation :
a
n
a_n
an
=
=
=
6
a
n
−
1
6a_{n-1}
6an−1
+
+
+
8
n
−
1
8^{n-1}
8n−1
initial value :
a
1
=
7
a_1 = 7
a1=7
The general term formula for solving the above recursive equation :
a
n
=
6
n
+
8
n
2
a_n = \cfrac{6^n + 8^n}{2}
an=26n+8n
Two 、 Summary of recursive equation examples
This problem is a specific counting problem , The above problem is not simply counting ,
This count has parameters
n
n
n ,
This type of counting , Can be seen as a Sequence count result ,
If you can find the sequence , consequent , the aforesaid , Dependency of ,
And know initial value ,
Can Solve the general term formula of the sequence ,
The general term formula just corresponds to the counting result ;
边栏推荐
- IDEA-配置插件
- Leetcode binary search tree
- 【剑指 Offer】58 - II. 左旋转字符串
- (Supplement) double pointer topic
- Using optimistic lock and pessimistic lock in MySQL to realize distributed lock
- 在ntpdate同步时间的时候出现“the NTP socket is in use, exiting”
- TCP擁塞控制詳解 | 3. 設計空間
- Preventing/catching “IllegalArgumentException: parameter must be a descendant of this view” error
- NSQ源码安装运行过程
- 【剑指 Offer 】57 - II. 和为s的连续正数序列
猜你喜欢

CC2530 common registers for port initialization

utfwry. Dat PHP, about ThinkPHP's method of IP location using utfwry address Library

Add color to the interface automation test framework and realize the enterprise wechat test report

Daily code 300 lines learning notes day 10
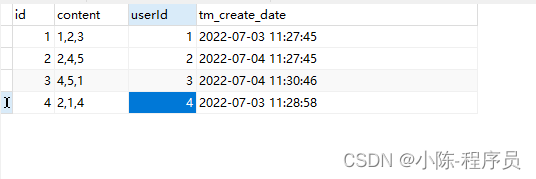
Mysql 将逗号隔开的属性字段数据由列转行
QT串口ui设计和解决显示中文乱码
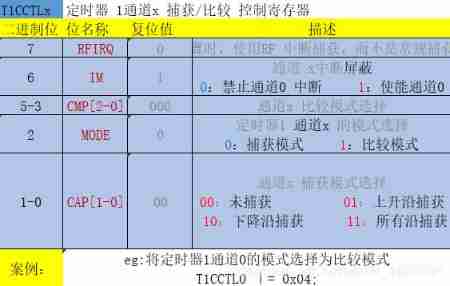
CC2530 common registers for timer 1
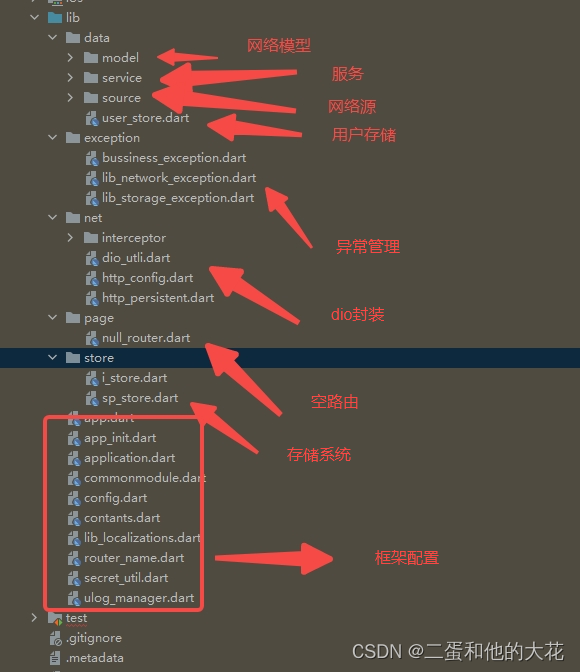
Learn from me about the enterprise flutter project: simplified framework demo reference

A survey of state of the art on visual slam
消息队列消息丢失和消息重复发送的处理策略
随机推荐
Processing strategy of message queue message loss and repeated message sending
手机注册股票开户安全吗 开户需要钱吗
What material is sa537cl2? Analysis of mechanical properties of American standard container plate
Yu Wenwen, Hu Xia and other stars take you to play with the party. Pipi app ignites your summer
A survey of state of the art on visual slam
One article takes you to understand machine learning
The word backspace key cannot delete the selected text, so you can only press Delete
Summary of three methods of PHP looping through arrays list (), each (), and while
nifi从入门到实战(保姆级教程)——flow
特征多项式与常系数齐次线性递推
[Jianzhi offer] 64 Find 1+2+... +n
CC2530 common registers for timer 1
8 cool visual charts to quickly write the visual analysis report that the boss likes to see
PHP CI (CodeIgniter) log level setting
利用MySQL中的乐观锁和悲观锁实现分布式锁
跟我学企业级flutter项目:简化框架demo参考
function overloading
2022.02.14_ Daily question leetcode five hundred and forty
Characteristic polynomial and constant coefficient homogeneous linear recurrence
MongoDB 的安装和基本操作