当前位置:网站首页>[combinatorial mathematics] recursive equation (example of recursive equation 2 Hanoi Tower | example of recursive equation 3 insertion sequencing)
[combinatorial mathematics] recursive equation (example of recursive equation 2 Hanoi Tower | example of recursive equation 3 insertion sequencing)
2022-07-03 16:48:00 【Programmer community】
List of articles
- One 、 Examples of recursive equations 2 Hanoi
- Two 、 Examples of recursive equations 3 Insertion sort
One 、 Examples of recursive equations 2 Hanoi
Hanoi problem :
- The recurrence equation is :
T
(
n
)
=
2
T
(
n
−
1
)
+
1
T(n) =2 T(n-1) + 1
T(n)=2T(n−1)+1
- initial value :
T
(
1
)
=
1
T(1) = 1
T(1)=1
- Explain :
T
(
n
)
=
2
n
−
1
T(n) = 2^n - 1
T(n)=2n−1
The recurrence equation represents , take
n
n
n The number of times a plate moves
T
(
n
)
T(n)
T(n) , And
n
−
1
n-1
n−1 The number of times a plate moves
T
(
n
−
1
)
T(n-1)
T(n−1) The relationship between ;
Solution reference : 【 Combinatorial mathematics 】 Recurrence equation ( Examples of special solutions ) One 、 Special solution example 1 ( Hanoi )
Two 、 Examples of recursive equations 3 Insertion sort
W
(
n
)
W(n)
W(n) Indicates the number of times to insert a sort in the worst case ;
Ahead
n
−
1
n-1
n−1 The number has been arranged , In the worst case, the number of insertion sorts is
W
(
n
−
1
)
W(n-1)
W(n−1) Time ,
The first
n
n
n A number should be inserted here
n
−
1
n-1
n−1 Of the numbers , The worst case scenario is The number to be inserted should be the same as all the sorted numbers
n
−
1
n-1
n−1 Compare two numbers , The number of comparisons is
n
−
1
n-1
n−1 Time ,
So the recurrence equation can be written as :
W
(
n
)
=
W
(
n
−
1
)
+
n
−
1
W(n) = W(n-1) + n-1
W(n)=W(n−1)+n−1
Initial value of recurrence equation :
W
(
1
)
=
0
W(1) = 0
W(1)=0 , If there is only one number , No sorting , The number of comparisons is
0
0
0 ;
The final solution is :
W
(
n
)
=
O
(
n
2
)
W(n) = O(n^2)
W(n)=O(n2) , The exact value is
W
(
n
)
=
n
(
n
−
1
)
2
W(n) = \cfrac{n(n-1)}{2}
W(n)=2n(n−1)
边栏推荐
- 什么是质押池,如何进行质押呢?
- 斑马识别成狗,AI犯错的原因被斯坦福找到了
- Processing strategy of message queue message loss and repeated message sending
- Mysql database DDL and DML
- LeetCode 1656. Design ordered flow
- CC2530 common registers
- [combinatorics] recursive equation (outline of recursive equation content | definition of recursive equation | example description of recursive equation | Fibonacci Series)
- [Jianzhi offer] 64 Find 1+2+... +n
- Basis of target detection (IOU)
- IDEA-配置插件
猜你喜欢

Add color to the interface automation test framework and realize the enterprise wechat test report

2022爱分析· 国央企数字化厂商全景报告

What kind of material is 14Cr1MoR? Analysis of chemical composition and mechanical properties of 14Cr1MoR

什么是质押池,如何进行质押呢?

Daily code 300 lines learning notes day 10
2022.02.14_ Daily question leetcode five hundred and forty
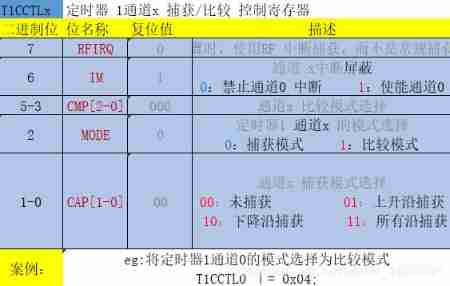
CC2530 common registers for timer 1

CC2530 common registers for port initialization
为抵制 7-Zip,列出 “三宗罪” ?网友:“第3个才是重点吧?”

CC2530 common registers for crystal oscillator settings
随机推荐
What material is 12cr1movr? Chemical property analysis of pressure vessel steel plate 12cr1movr
Learn from me about the enterprise flutter project: simplified framework demo reference
[Jianzhi offer] 64 Find 1+2+... +n
Idea configuration plug-in
word 退格键删除不了选中文本,只能按delete
Kotlin学习快速入门(7)——扩展的妙用
CC2530 common registers for crystal oscillator settings
Necessary ability of data analysis
Informatics Olympiad all in one YBT 1175: divide by 13 | openjudge noi 1.13 27: divide by 13
Is it safe to open a stock account by mobile registration? Does it need money to open an account
AcWing 第58 场周赛
Everyone in remote office works together to realize cooperative editing of materials and development of documents | community essay solicitation
Execute script unrecognized \r
MySQL Basics
Golang decorator mode and its use in NSQ
Network security web penetration technology
Overview of satellite navigation system
【剑指 Offer 】64. 求1+2+…+n
Capacités nécessaires à l'analyse des données
utfwry. Dat PHP, about ThinkPHP's method of IP location using utfwry address Library