当前位置:网站首页>LeetCode·72.编辑距离·动态规划
LeetCode·72.编辑距离·动态规划
2022-08-03 16:30:00 【小迅想变强】
链接:https://leetcode.cn/problems/edit-distance/solution/by-xun-ge-v-7g4m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
题目
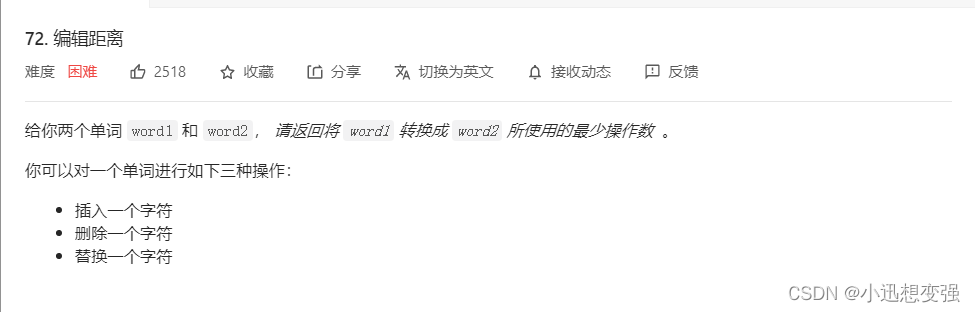
示例
思路
解题思路
动态规划
定义dp[i][j]数组表示word1中前 i 个字符 转换为 word2 中前 j 个字符所需要的步数
- 当 word1[i] == word2[j]时,我们不需要进行然后操作所以 dp[i][j] = dp[i-1][j-1]
- 当 word1[i] != word2[j]时,我们需要对当前位置进行调整,使得两个元素相等,存在三种调整方式
- dp[i-1][j-1] 表示替换操作
- dp[i-1][j] 表示删除操作
- dp[i][j-1] 表示插入操作
我们取这三种方式中操作数最少的数更新为当前操作步数即可
内存优化
从上面思路来看,我们在计算当前位置操作数时,只需要用到dp[i-1][j] , dp[i][j-1] , dp[i-1][j-1],分别为当前位置的上方,左边,左上角,那么我们可以将二维空间转换为一维,对于dp[i-1][j] -> 当前一维空间未更新之前的dp[j] , dp[i][j-1] -> 当前一维空间更新之后的dp[j-1], 那么dp[i-1][j-1]不好表示,我们申请一个变量临时保存他,然后动态更新即可
代码
动态规划内存优化
#define MIN(a , b , c) (((a) < (b) ? (a) : (b)) < (c) ? ((a) < (b) ? (a) : (b)) : (c))
int minDistance(char * word1, char * word2){
int len1 = strlen(word1);
int len2 = strlen(word2);
int dp[len2+1];//初始化
for(int i = 0; i < len2+1; i++)//初始化一维空间
{
dp[i] = i;
}
int s = dp[0];//临时变量保存dp【i-1】【j-1】
for(int i = 0; i < len1; i++)
{
for(int j = 1; j <= len2; j++)
{
int t = dp[j];//动态更新保存dp[i-1][j-1]
if(word1[i] == word2[j-1])
{
dp[j] = s;
}
else
{
dp[j] = MIN(dp[j] , dp[j-1] , s) + 1;
}
s = t;//更新dp[i-1][j-1]
}
dp[0]++;
s = dp[0];
}
return dp[len2];
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/edit-distance/solution/by-xun-ge-v-7g4m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。动态规划
#define MIN(a , b , c) (((a) < (b) ? (a) : (b)) < (c) ? ((a) < (b) ? (a) : (b)) : (c))
int minDistance(char * word1, char * word2){
int len1 = strlen(word1);
int len2 = strlen(word2);
int dp[len1+1][len2+1];
for(int i = 0; i < len1+1; i++)
{
dp[i][0] = i;
}
for(int i = 0; i < len2+1; i++)
{
dp[0][i] = i;
}
for(int i = 1; i <= len1; i++)
{
for(int j = 1; j <= len2; j++)
{
if(word1[i-1] == word2[j-1])
{
dp[i][j] = dp[i-1][j-1];
}
else
{
dp[i][j] = MIN(dp[i-1][j] , dp[i][j-1] , dp[i-1][j-1]) + 1;
}
}
}
return dp[len1][len2];
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/edit-distance/solution/by-xun-ge-v-7g4m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。边栏推荐
- C专家编程 第2章 这不是Bug,而是语言特性 2.3 误做之过
- Kubernetes 笔记 / 任务 / 管理集群 / 用 kubeadm 管理集群 / 配置一个 cgroup 驱动
- C专家编程 第3章 分析C语言的声明 3.1 只有编译器才会喜欢的语法
- C专家编程 第2章 这不是Bug,而是语言特性 2.1 这关语言特性何事,在Fortran里这就是Bug呀
- 通俗理解apt-get 和pip的区别是什么
- TCP 可靠吗?为什么?
- 滑环安装注意事项
- uniapp的webview滑动缩放
- TypeScript文件的编译执行
- error:Illegal instruction (core dumped),离线下载安装这个other版本numpy
猜你喜欢

罗克韦尔AB PLC RSLogix5000中创建新项目、任务、程序和例程的具体方法和步骤
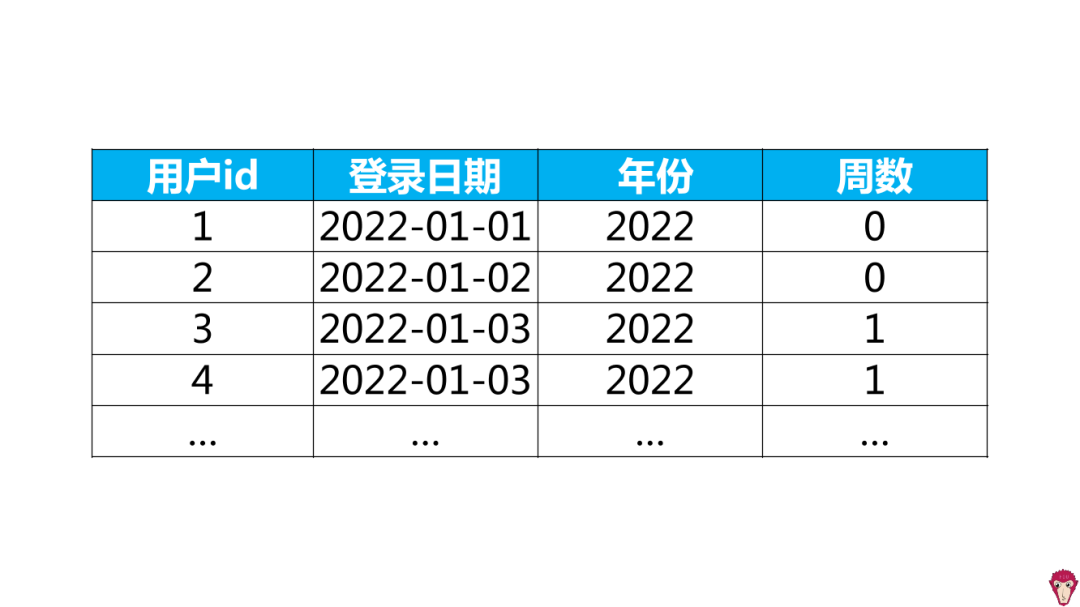
How to analyze the weekly activity rate?
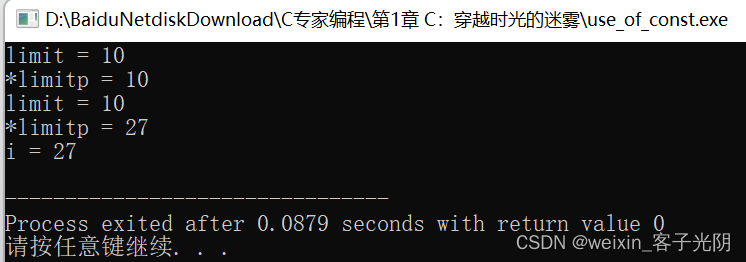
C专家编程 第1章 C:穿越时空的迷雾 1.9 阅读ANSI C标准,寻找乐趣和裨益
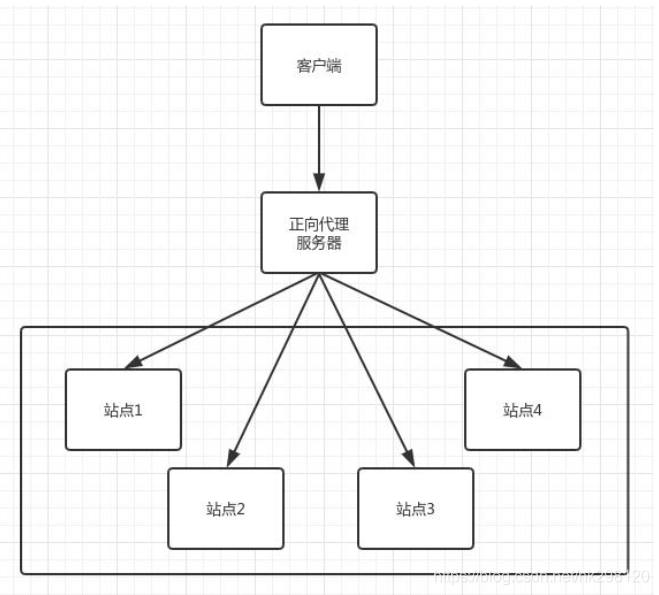
正向代理与反向代理

中小微企业如何简单便捷、低成本实现数字化?360视觉云有妙招
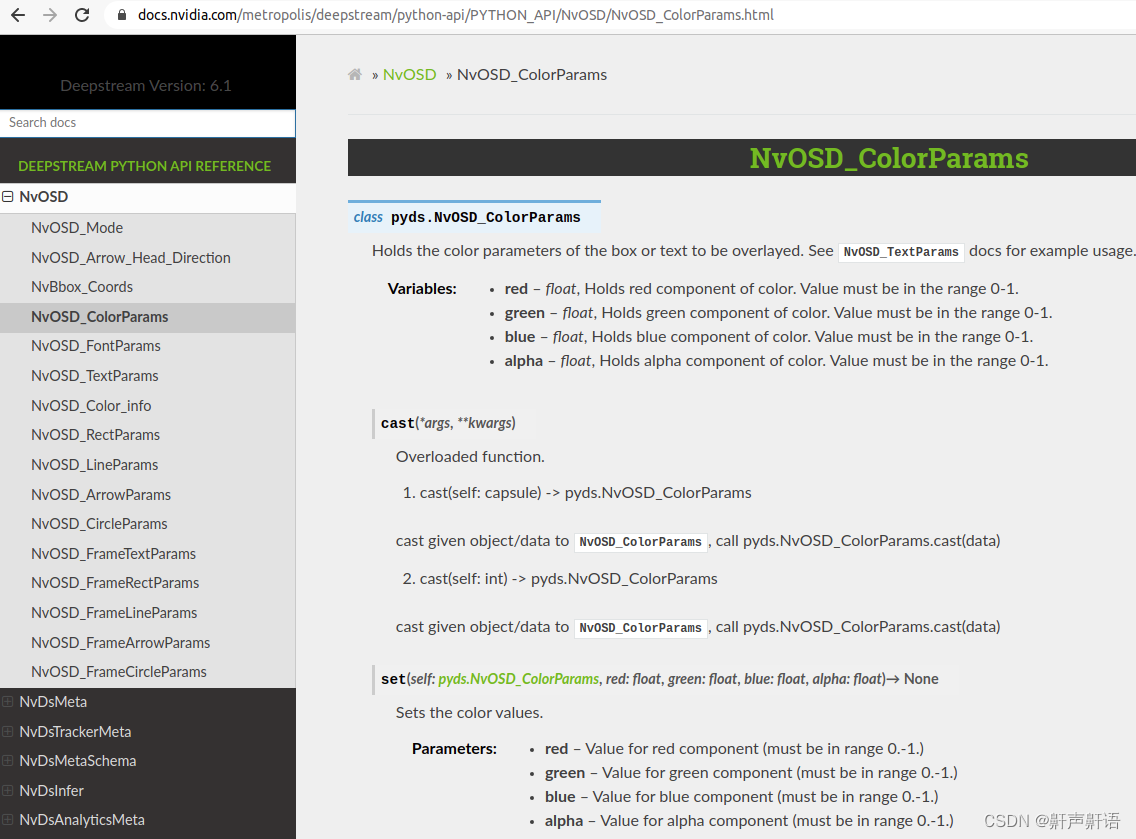
deepstresam的插件配置说明,通过配置osd,设置字体的背景为透明

蒋松廷 荣获第六季完美童模全球总决赛 全球总冠军
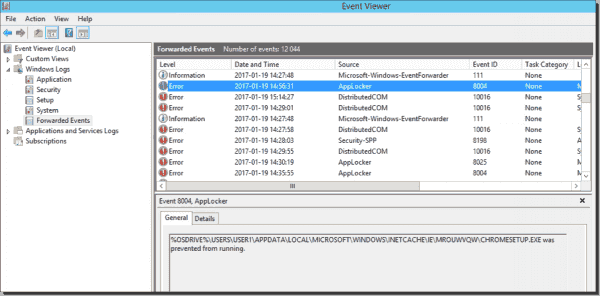
Windows 事件转发到 SQL 数据库
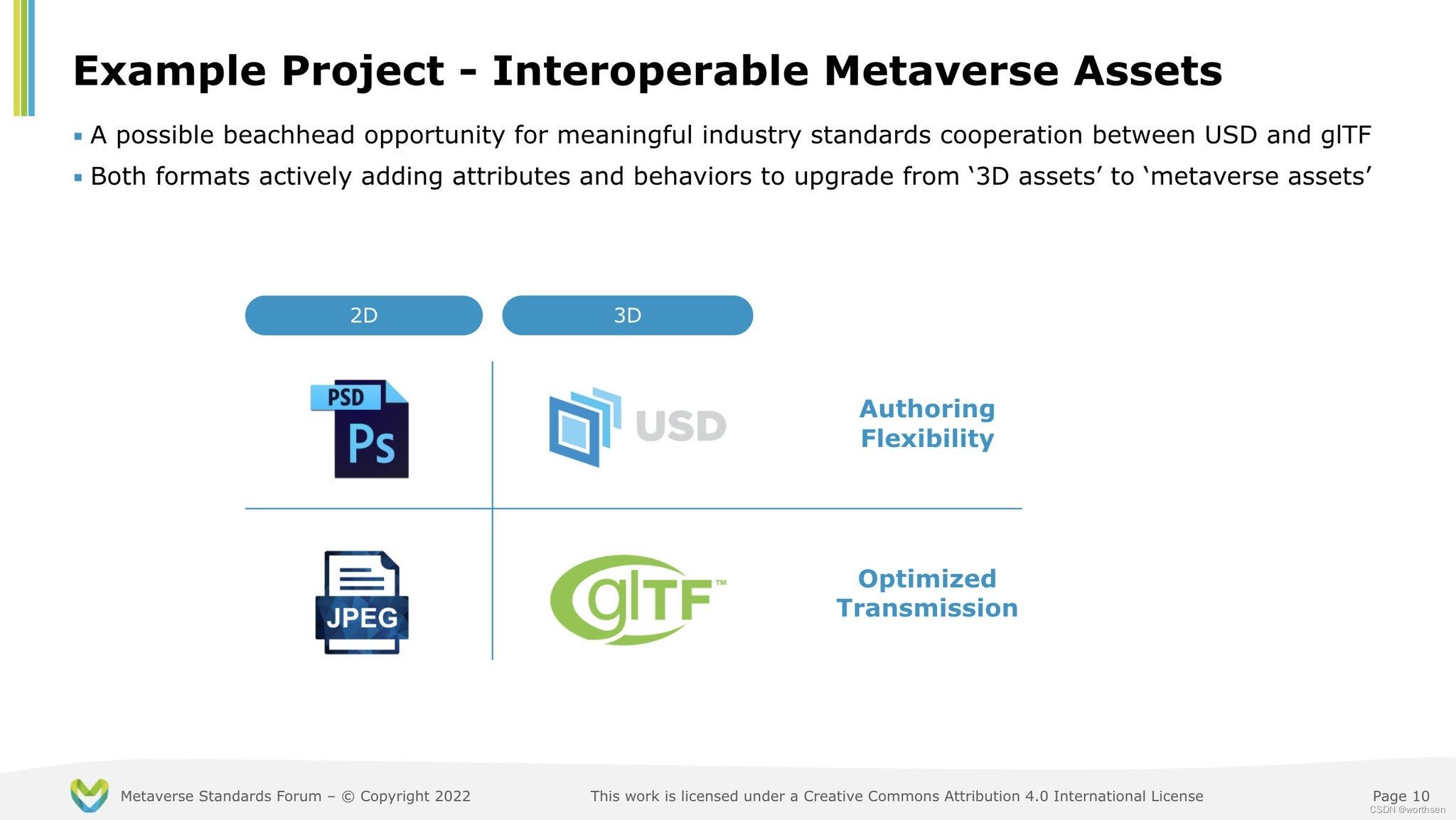
机器人开发--Universal Scene Description(USD)
Component communication - parent-child component communication
随机推荐
TypeScript文件的编译执行
C专家编程 第3章 分析C语言的声明 3.5 typedef可以成为你的朋友
黄致绮 荣获第六季完美童模全球总决赛 全国总冠军
Cookie和Session的关系
设置海思芯片MMZ内存、OS内存详解
Components of communication - the drop-down menu
C语言02、语句、函数
面试突击71:GET 和 POST 有什么区别?
Looking at the ecological potential of Hongmeng OS from the evolution of MatePad Pro
世界顶级级架构师编写2580页DDD领域驱动设计笔记,属实有牌面
请问下这个hologres维表是被缓存了么?怎么直接Finished了
Leetcode76. Minimal Covering Substring
C# 获取文件名和扩展名(后缀名)
C专家编程 第3章 分析C语言的声明 3.6 typedef int x[10]和#define x int[10]的区别
【带你了解SDN和网络虚拟化】
MATLAB | 七夕节快到了,还不给朋友安排上这个咕呱小青蛙?
如何使用MATLAB绘制极坐标堆叠柱状图
MobileVIT实战:使用MobileVIT实现图像分类
[Unity Getting Started Plan] Basic Concepts (8) - Tile Map TileMap 01
[Unity Getting Started Plan] Basic Concepts (7) - Input Manager & Input Class