【CCPC】2020CCPC长春 F - Strange Memory | 树上启发式合并(dsu on a tree)、主席树

想让APP和微信一样，可以流畅运行小程序？ | 体验即送大疆、华为、樱桃键盘！>>>

人均会dsu的赛区..早知道就把数组开大一点了..

差20分钟就银了呀..

最后一场ccpc留下遗憾了...

题目大意：

给出一个树

让你求出：

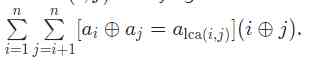
题目思路：

看到lca，那就只能是枚举每个点作为lca的贡献

所以枚举当前节点作为lca时，所以能够产生贡献的就是，他的任意两棵子树的贡献

所以直接枚举当前这个子树的所有点，然后和之前的权值去匹配

这里需要按位拆分一下：

a^(b+c) != a^b + a^c

但是把数按位拆分之后，对于当前lca权值是ai = c，当前点是ak = a，对于之前所有子树内权值a^c的点，如果k的第x位是1，那么就看一下a^c的点中 有多少个在第k位是0，反之亦然

这样就可以把贡献求出来了

此时就需要一个操作：

求出权值为 c 的第k位 是1的数量

这个地方好像可以用unorder_map 或者 multiset 解决掉

但是比赛时太保险了...加了主席树..(可能不保险莽一波 就不同结果了)

至于这里的启发式合并无非就是类似哈夫曼树的原理:

让节点个数最大的子树只访问一次，但是这里有一个点，如果给出的树是一条链的话，还是会被卡成n^2/2，但是需要注意一个细节点：不可能有ai = ai^aj的情况，因为aj一定大于0

所以此时就可以直接排除链的情况把复杂度 总体控制到O(nlogn)

加个主席树以后总体复杂度：O(nlog^n)

Code:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5+6;
const int mod = 1e9+7;
const ll base = 1e9;
ll n,m,p;
ll a[maxn];
int L[maxn],R[maxn];
int cnt = 0;
vector<int>v[maxn];
vector< pair<int,int> >g[maxn];
struct node{
    int v[22],w;///第k位的数量
    int l,r;
}t[maxn*21];
int root[maxn];
int sz[maxn];
int cot = 0;
void Insert(int &x,int y,int l,int r,int pos,ll w){
    x = ++cnt;
    t[x] = t[y];
    for(int i=0;i<=20;i++)
        if(w>>i&1) t[x].v[i]++;
    t[x].w ++;
    if(l == r) return ;
    int mid = (l+r)/2;
    if(pos<=mid) Insert(t[x].l,t[y].l,l,mid,pos,w);
    else Insert(t[x].r,t[y].r,mid+1,r,pos,w);
}
ll Query(int x,int y,int l,int r,int pos,ll w){
    if(l == r){
        ll ans = 0;
        for(int i=0;i<=20;i++){
            if(w>>i&1)
                ans += ( (t[y].w - t[x].w) - (t[y].v[i]-t[x].v[i]) )*(1<<i);
            else
                ans += (t[y].v[i] - t[x].v[i])*(1ll<<i);
        }
        return ans;
    }
    int mid = (l+r)/2;
    if(pos <= mid) return Query(t[x].l,t[y].l,l,mid,pos,w);
    return Query(t[x].r,t[y].r,mid+1,r,pos,w);
}

void dfs(int u,int fa){
    sz[u] = 1;
    for(int e:v[u]){
        if(e == fa) continue;
        dfs(e,u);
        g[u].push_back({sz[e],e});
        sz[u] += sz[e];
    }
    sort(g[u].begin(),g[u].end());
}

void dfs1(int u){
    int sz = g[u].size();
    L[u] = ++cot;
    Insert(root[cot],root[cot-1],0,1e6,a[u],u);
    for(int i=sz-1;i>=0;i--){
        int e = g[u][i].second;
        dfs1(e);
    }
    R[u] = cot;
}

ll res = 0;
ll work(int u,int R,int L,int x){
    ll temp = 0;
    if(a[u]^x||a[u]^x<=1e6)
        temp += Query(root[L-1],root[R],0,1e6,a[u]^x,u);
    for(auto tempx:g[u])  temp += work(tempx.second,R,L,x);
    return temp;
}

void dfs2(int u){
    int sz = g[u].size();
    int pre = L[u],last = R[u];
    for(int i=sz-2;i>=0;i--){
        last = R[g[u][i+1].second];
        res += work(g[u][i].second,last,pre,a[u]);
    }
    for(int i=sz-1;i>=0;i--) dfs2(g[u][i].second);
}
int main(){

    scanf("%lld",&n);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    for(int i=1;i<=n-1;i++){
        int x,y;scanf("%d%d",&x,&y);
        v[x].push_back(y);
        v[y].push_back(x);
    }

    dfs(1,1);
    dfs1(1);
    dfs2(1);
    printf("%lld\n",res);
    return 0;
}
/**
6
4 2 1 6 6 5
1 2
2 3
1 4
4 5
4 6
**/