[paper reading notes] network embedding with attribute refinement

[ Paper reading notes ] Network Embedding with Attribute Refinement

---

The structure of this paper

1. solve the problem
2. Main contributions
3. Algorithm principle
4. reference

---

(1) solve the problem

According to the homogeneity Hypothesis , Similar nodes tend to be linked together , Nodes with similar properties are also topologically connected by . But some of the properties of real networks are not very good , namely Node attributes and topology are often inconsistent , This makes some pairs of nodes similar in topology , But it's not necessarily the same in node properties , vice versa .

---

(2) Main contributions

Contribution 1： It is found that the node attribute is inconsistent with the node topology .

Contribution 2： A novel unsupervised framework is proposed NEAR, It uses an attribute filter guided by homogeneity to optimize the attributes and solve the inconsistency between node attributes and node topology , So as to improve the accuracy of attribute network representation .

---

(3) Algorithm principle

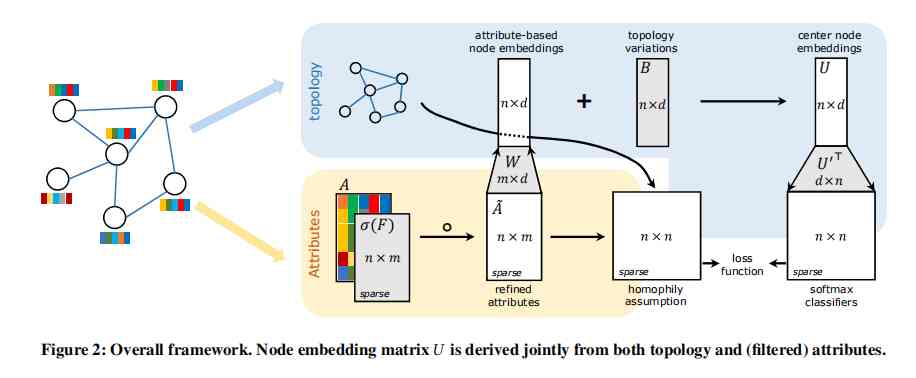
NEAR The main framework of the algorithm is shown in the figure below ： From the frame diagram, we can see the general idea of the algorithm ：（ Firstly, it is clear that the parameters to be learned by the network are filters F、 Hidden layer weight matrix W、 Topological information matrix B And the node context vector U'） Second, let's look at the introduction of attribute information , Attribute matrix A With a filter F The optimized data matrix is obtained by multiplication A~,A~ And the corresponding weight matrix in the network W Multiply to get a n x d Attribute based node representation vector matrix , Plus the bias matrix in the network B（ Represents the network embedding matrix based on topology information ） We can get the node center vector （ The nodes in the neural network are represented by two vectors , Center node vector and context vector , Analogy to Skip-Gram）, The node center vector matrix and the node context vector matrix get a similar node similarity matrix , Again softmax Normalization can predict the possible context of the central node （ namely Skip-Gram Model ）, The loss function of this part is Skip-Gram Loss function of （ Maximize the co-occurrence probability of nodes ）. also , Let's look at the introduction of topological information , Topology information is used to calculate the node similarity matrix n x n （ Introduction ） And A~ Attribute matrix n x n combination , As a term in the loss function . You can see , The final loss function consists of two parts ,Skip-Gram Loss function + Based on the homogeneity assumption, it is used to optimize the node properties （ Solve the problem of inconsistent properties and topology ） Loss function （ Introduction ）. About the network training part , Training samples are generated either by sampling neighbors or by random walk .

The loss function consists of two parts , The following is an introduction to each part ：

• Skip-Gram The loss function is as follows （ The detailed derivation process is shown in DeepWalk The original paper ）： Minimizing the objective function is to find the node vector , It maximizes the co-occurrence probability of nodes in the window .

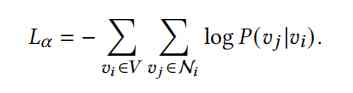
• Based on the homogeneity assumption, it is used to optimize the node properties （ Solve the problem of inconsistent properties and topology ） Loss function ： sim_t It is the similarity of node pairs in topology （ The homogeneity hypothesis can be expressed by the similarity of nodes' neighborhood ）, In this paper, I use Adar index To measure （ The two nodes Adar index Measurement calculation ： Of all the common neighbors of two nodes logk Divided 1 Sum up ）.sim_a Is the attribute similarity of a node pair , In this paper, the cosine of node attribute vector is used to measure . Then minimize the following objective function to express the meaning of ： somehow （ Such as filter F） Adjust the attribute vector of the node pair , The product of structural similarity and attribute similarity of node pairs is the largest （ It's the biggest when it's equal ）, This ensures that the nodes are in the structure （ attribute ） Similar at the same time in the properties （ structure ） It's similar to , That is to solve the problem of inconsistency between node attribute and node topology .

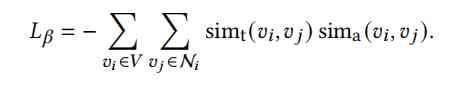
The final objective function is as follows （ Weighted sum of the above two objective functions ）：

---

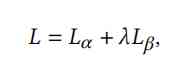
(4) reference

Xiao T, Fang Y, Yang H, et al. Network Embedding with Attribute Refinement[J].

---