[paper reading notes] a multilayered informational random walk for attributed social network embedding

[ Paper reading notes ] A Multilayered Informative Random Walk for Attributed Social Network Embedding

---

The structure of this paper

1. solve the problem
2. Main contributions
3. Algorithm principle
4. reference

---

(1) solve the problem

Most of the existing unsupervised attribute network representation algorithms don't distinguish the information content of node edge structure and attribute . namely , Sometimes two nodes have no edges in topology , But it's very similar in properties （ The inconsistency of node topology and attributes ）.

---

(2) Main contributions

Contribution 1： Put forward MIRand（ Random walk of multi-layer information ） Method , This method first constructs a multilevel graph , Secondly, we use a novel random walk （ Based on the amount of information , The node structure and properties are considered ） Jump to capture features in a multi-level graph . This is the first attribute network representation learning algorithm using multi-layer graph random walk .（ One layer corresponds to the structure , Another layer deals with the attributes associated with nodes ）. Other non attribute network representation algorithms based on random walk can also be extended to attribute network representation .

---

(3) Algorithm principle

It is proposed in the paper that MIRand The algorithm includes the following three parts ：

1. Network layering （ Structure layer and attribute layer ）.
2. Random walk of multi-layer graph based on node information .
3. adopt Skip-Gram Model to learn the vector representation of nodes .

The following is from MIRand Each part of the algorithm is described separately ：

• First step , Network layering （ Structure layer and attribute layer ）： The structural layer is very simple , The topology of the original network （ Edge graph ） It's the structure of the network . The edge in the attribute graph can be constructed by calculating the attribute similarity of the nodes, so as to construct the attribute graph , However, it is very expensive to calculate the attribute similarity of all nodes in the network , So only each node is calculated θ x Average degree The node with the largest cosine similarity is connected to the edge , Thus the attribute graph is constructed .

• The second step , Random walk of multi-layer graph based on node information ： The random walk will jump and walk on the attribute map and structure diagram . When random walk reaches the node v_i When , Our goal is to choose to jump to structure or attribute graph based on the amount of information in the corresponding layer . So how to calculate the information of nodes in the structure layer or attribute layer ？ The author thinks that in random walk, we should try our best to transfer to those nodes which only have strong link relationship with a few neighbors , Because these nodes with strong link relationship have higher confidence in similarity . In this paper, we assume that the edge whose edge weight is greater than the average edge weight in the network is a strong link edge . The nodes with strong link edges in the network are strong link neighbors of each other .（ Strong linked neighbors are defined in both structure and attribute graphs ） We define nodes separately v_i The amount of information in the structure diagram and in the attribute diagram is shown in the following formula . The more strongly linked neighbors , The less information it has （ The node with low degree of information is high , The probability of similarity between these nodes and their neighbors is also greater than that of high nodes ）.
  
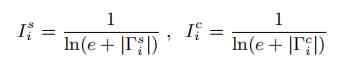
  According to the amount of information of the current node, we can define the transition probability between layers , That is, according to probability, the next node will jump in the structure diagram or in the attribute graph . What about the transition probability of nodes in the inner layer , As shown in the following formula ：
  
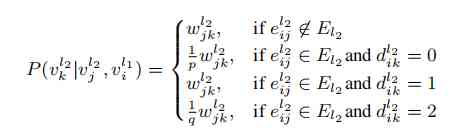
  The above intra layer transfer probability can be divided into two cases .
  (1) If node i And nodes j stay l2 If there is no edge in the layer , Then the next hop selects nodes according to probability j The most powerful neighbor .(2) If node i and j Have edge , Then press node2vec The way to swim .
  The inter layer transfer probability and the intra layer transfer probability are described above , Now the random walk based on the amount of information should have been understood ！！！
  （MIRand It can be extended to networks with multiple types of properties , Design more layers , Then use the amount of information to jump between layers .）

• The third step , Follow step three Skip-Gram Learning nodes represent vectors （ I won't repeat ）.

---

(4) reference

Bandyopadhyay S, Biswas A, Kara H, et al. A Multilayered Informative Random Walk for Attributed Social Network Embedding[J].

---