[paper reading notes] rosane, robust and scalable attributed network embedding for sparse networks

[ Paper reading notes ] RoSANE: Robust and scalable attributed network embedding for sparse networks

---

The structure of this paper

1. solve the problem
2. Main contributions
3. Algorithm principle
4. reference

---

(1) solve the problem

• Most of the existing ANE (attributed network embedding) The algorithm does not consider the problem caused by sparse network （ Still using edges to handle node properties , And there are very few edges in the sparse network , There is limited information available ）.
• existing ANE The scalability of the algorithm （ Some attribute network representation frameworks still have time complexity relative to the number of nodes of square level or cubic level ）.
• There are some ANE The robustness of the algorithm for different networks is relatively low , To ensure that the parameters of the algorithm are better adjusted in different networks, it can be better applied to scale networks （ The parameters of some algorithms need mesh optimization , It's very expensive . It's hard to adapt to the reality ）.

---

(2) Main contributions

Contribution 1： This paper discusses in detail the problems of different kinds of algorithms in dealing with sparse networks .

ANE There are four kinds of algorithms ：

• Based on convex optimization ( Matrix decomposition ): Finally, a matrix factorization operation is required , It's very time consuming , So the algorithm can not be applied to large-scale networks .
• Based on graph convolution network : GCN、graphSAGE Rely on edges to aggregate node attributes , The performance may be lower in sparse networks .GRCN The similarity of node attributes is fused into the adjacency matrix of nodes , Second, use GCN、graphSAGE A similar approach to network representation . However, the accurate calculation of node attribute similarity needs the complexity of the third power of node number .
• Based on deep neural network ： Although it can well mine nonlinear relations , However, the computational complexity is relatively high .
• Based on random walk method ： On a network with sparse edges , Random walk can capture very few node relationships .

Contribution 2： Put forward a novel ANE Method RoSANE, That is to construct and integrate the topological structure and attribute transfer matrix , The transition probability matrix is used to guide random walks on graphs , It is equivalent to reconstructing a dense network which combines the topology and attribute information of nodes and makes network representation on the basis of the network .

---

(3) Algorithm principle

RoSANE The main framework of the algorithm is shown in the figure below ： Suppose there are multiple sources of information S, The proposed method constructs node transition probability matrix for each information source T , And the transfer probability matrix of multiple nodes is fused into a unified node transition probability matrix （ It is equivalent to the fusion of multi-party information to reconstruct a more dense network ）, The transition probability matrix is used to realize random walk on the graph , Finally, using the representation model Skip-Gram Node vector training .

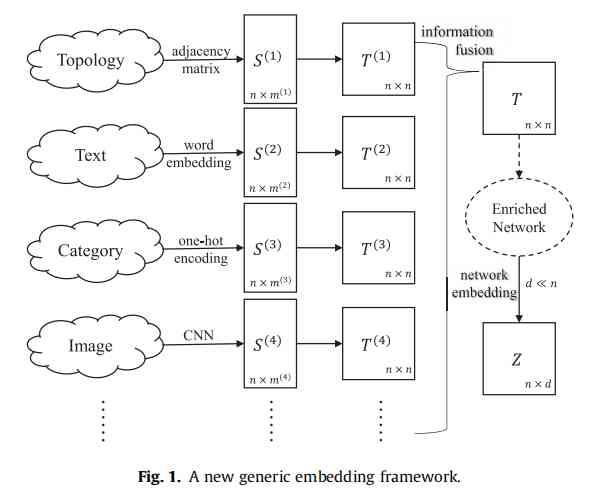
The following is the use of topology information and node attribute information to elaborate the details of the above framework ：

• First step , Topological information transfer probability matrix construction ： As shown in the following formula , It is equivalent to doing a simple row normalization to get the topological information transfer probability matrix , The greater the edge weight, the greater the transfer probability .

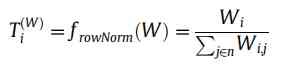
• The second step , Attribute information transfer probability matrix construction ： In order to avoid computing the attribute similarity of all nodes in the network （ If complete calculation, the node attribute similarity matrix will have n Square non-zero elements ）, The algorithm uses a ball tree K The nearest neighbor technique is used to construct the most similar properties of each node k A neighbor （ In this way, the node attribute similarity matrix will only have n x k A non-zero element ）,k The nearest neighbor uses cosine function to measure the matrix of node attribute vector . Get only n x k After the attribute similarity matrix of non-zero elements , The node attribute information transfer probability matrix can be obtained by normalizing the matrix row , The greater the attribute similarity, the greater the transfer probability .

• The third step , Information fusion （ The final transition probability matrix is constructed by integrating the node topology transition matrix and the attribute transition matrix T）： As shown in the following formula ,T(W) and T(X) They are node topology transition matrix and node attribute transfer matrix . The following formula means , If a node has no edges with other nodes in Topology （ Isolated point ）, Then the node jumps according to the attribute transfer probability matrix . Otherwise, the topological transition matrix and the attribute transfer matrix are considered （ To sum by weight ）.

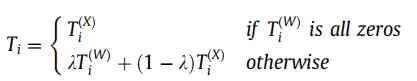
• Step four , Follow step three Skip-Gram Learning nodes represent vectors （ I won't repeat ）.

---

(4) reference

Hou, Chengbin, Shan He, and Ke Tang. "RoSANE: Robust and scalable attributed network embedding for sparse networks." Neurocomputing 409 (2020): 231-243.

---