当前位置:网站首页>【luogu P8326】Fliper(图论)(构造)(欧拉回路)
【luogu P8326】Fliper(图论)(构造)(欧拉回路)
2022-07-31 16:30:00 【SSL_TJH】
Fliper
题目链接:luogu P8326
题目大意
平面上有 n 个挡板(分左上到右下和右上到左下),如果小球碰到会 90 度改变轨迹。
然后你要给每个挡板一个颜色,使得对于每个循环的反弹序列,满足每个颜色的挡板出现次数相同而且是偶数。(如果一个挡板在序列中出现两次算两次)
如果无法构造方案输出 -1。
思路
首先考虑找出循环。
那就是把一个挡板分成两个点(两面),然后连一个同色边表示这个边的颜色确定挡板的颜色。
然后你把从一面弹回到令一个地方的一个面的两个点连边,然后把这个给缩点一下。
那就会形成一些大点(表示循环序列),以及一些其他的点(不在循环序列中),那我们把它连向一个 i n f \rm inf inf 点。
然后考虑染色,会发现你要满足所有的循环序列,如果暴力搞可以解方程但是复杂度也太大了。
考虑找点性质,那这是一个图我们就找点图论的性质。
发现有解的情况我们看看是则那样的,不难想到情况是每个大点的度数要是 8 8 8 的倍数。
然后图论中有一个性质就是度数为奇数的点总是有偶数个的。
然后我们就可以得出 i n f \rm inf inf 点的度数一定也是偶数。(如果是奇数那就只有 1 1 1 个点,不是偶数个)
那不难想到一个东西叫做欧拉回路。
考虑找出欧拉回路然后黑白染色,那我们就分成了两种颜色。
那不难接下来想出分出四种的做法:因为这样之后度数是 4 4 4 的倍数,所以也是存在欧拉回路的。(根据上面的图论性质也会有 i n f \rm inf inf 点度数为偶数)
那我们就对分出的两个颜色的图分别再跑一个欧拉回路,就分成四种了。
代码
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 5e5 + 1000;
/* op=0: / , op=1: \ */
/* i / n+i i \ n+i */
struct node {
int x, y, op, id;
}a[N];
int n, col[N * 2], tot;
int ans[N], KK_, sta[N * 2], du[N * 2];
vector <int> G[N * 2], F[N * 2], F_[N * 2];
bool in[N * 2], use[N * 2];
int zf, re; char c;
int read() {
zf = 1; re = 0; c = getchar();
while (c < '0' || c > '9') {
if (c == '-') zf = -zf;
c = getchar();
}
while (c >= '0' && c <= '9') {
re = (re << 3) + (re << 1) + c - '0';
c = getchar();
}
return re * zf;
}
bool cmpx(node x, node y) {
if (x.x != y.x) return x.x < y.x; return x.y < y.y;}
bool cmpy(node x, node y) {
if (x.y != y.y) return x.y < y.y; return x.x < y.x;}
void add(int x, int y) {
G[x].push_back(y); G[y].push_back(x);
}
//0:光线边
//1:同色边
//2:INF边
bool Find;
void dfs(int now, int father) {
sta[++sta[0]] = now; in[now] = 1;
for (int i = 0; i < G[now].size(); i++)
if (G[now][i] != father) {
if (in[G[now][i]]) {
tot++; Find = 1;
while (sta[0]) col[sta[sta[0]]] = tot, sta[0]--;
return ;
}
else dfs(G[now][i], now);
if (Find) return ;
}
}
void Add(int x, int y, int z) {
F[x].push_back(y); if (x != y) F[y].push_back(x);
F_[x].push_back(z); if (x != y) F_[y].push_back(z);
du[x]++; du[y]++;
}
void Link() {
sort(a + 1, a + n + 1, cmpy);
for (int L = 1, R; L <= n; L = R + 1) {
R = L; while (R < n && a[R + 1].y == a[L].y) R++;
for (int i = L; i < R; i++) {
add(n + a[i].id, a[i + 1].id);
}
}
sort(a + 1, a + n + 1, cmpx);
for (int L = 1, R; L <= n; L = R + 1) {
R = L; while (R < n && a[R + 1].x == a[L].x) R++;
for (int i = L; i < R; i++) {
if (a[i].op == 0 && a[i + 1].op == 0) add(a[i].id, n + a[i + 1].id);
if (a[i].op == 0 && a[i + 1].op == 1) add(a[i].id, a[i + 1].id);
if (a[i].op == 1 && a[i + 1].op == 0) add(n + a[i].id, n + a[i + 1].id);
if (a[i].op == 1 && a[i + 1].op == 1) add(n + a[i].id, a[i + 1].id);
}
}
for (int i = 1; i <= 2 * n; i++)
if (!in[i]) {
sta[0] = 0, Find = 0, dfs(i, 0);
if (!Find) {
while (sta[0]) use[sta[sta[0]]] = 1, sta[0]--;
}
}
for (int i = 1; i <= n; i++) {
int x = use[i] ? 2 * n + 1 : col[i];
int y = use[n + i] ? 2 * n + 1 : col[n + i];
Add(x, y, i);
}
}
bool check_ans() {
for (int i = 1; i <= tot; i++)
if (du[i] % 8 != 0) return 0;
return 1;
}
struct nde {
int id, to, nxt;
}e[N * 2];
int in_[N * 2], le[N * 2], KK;
void run_way(int now) {
for (int i = le[now]; i; i = le[now]) {
le[now] = e[i].nxt;
if (in_[e[i].id]) continue; in_[e[i].id] = 1;
run_way(e[i].to); sta[++sta[0]] = e[i].id;
}
}
void get_oula() {
memset(in_, 0, sizeof(in_)); sta[0] = 0;
run_way(2 * n + 1);
for (int i = 1; i <= tot; i++) run_way(i);
for (int i = 1; i <= sta[0]; i += 2)
in_[sta[i]]++;
}
void clear() {
KK = 0; memset(le, 0, sizeof(le));
}
void slove() {
clear();
for (int i = 1; i <= 2 * n + 1; i++)
for (int j = 0; j < F[i].size(); j++)
e[++KK] = (nde){
F_[i][j], F[i][j], le[i]}, le[i] = KK;
get_oula();
for (int i = 1; i <= n; i++) ans[i] = in_[i] * 2;
clear();
for (int i = 1; i <= 2 * n + 1; i++)
for (int j = 0; j < F[i].size(); j++)
if (ans[F_[i][j]] == 2)
e[++KK] = (nde){
F_[i][j], F[i][j], le[i]}, le[i] = KK;
get_oula();
for (int i = 1; i <= n; i++) if (in_[i]) ans[i] += in_[i] - 2;
clear();
for (int i = 1; i <= 2 * n + 1; i++)
for (int j = 0; j < F[i].size(); j++)
if (ans[F_[i][j]] == 4)
e[++KK] = (nde){
F_[i][j], F[i][j], le[i]}, le[i] = KK;
get_oula();
for (int i = 1; i <= n; i++) if (in_[i]) ans[i] += in_[i] - 2;
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
}
int main() {
// freopen("pinball.in", "r", stdin);
// freopen("pinball.out", "w", stdout);
n = read();
for (int i = 1; i <= n; i++) {
a[i].x = read(); a[i].y = read(); a[i].id = i;
char c = getchar(); while (c != '\\' && c != '/') c = getchar();
if (c == '/') a[i].op = 0; else a[i].op = 1;
}
Link();
if (!check_ans()) {
printf("-1"); return 0;}
slove();
return 0;
}
边栏推荐
- 牛客网刷题(三)
- ASP.NET Core generates continuous Guid
- C程序是如何跑起来的01 —— 普通可执行文件的构成
- flutter设置statusbar状态栏的背景颜色和 APP(AppBar)内部颜色一致方法。
- 动态规划之线性dp(上)
- Graham's Scan method for solving convex hull problems
- 【7.29】代码源 - 【排列】【石子游戏 II】【Cow and Snacks】【最小生成数】【数列】
- The new BMW 3 Series is on the market, with safety and comfort
- C language - function
- 【7.28】代码源 - 【Fence Painting】【合适数对(数据加强版)】
猜你喜欢
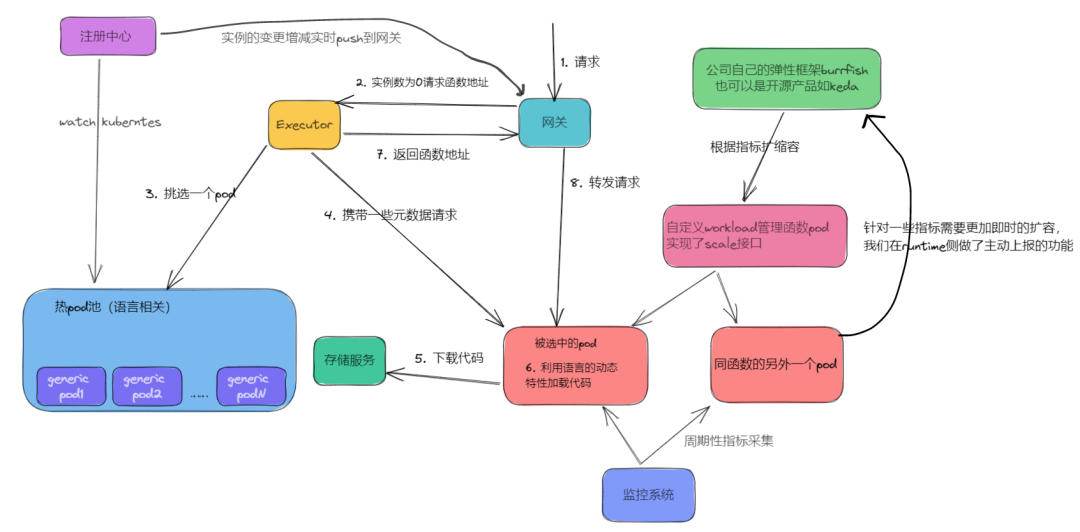
OPPO在FaaS领域的探索与思考
![[Meetup Preview] OpenMLDB+OneFlow: Link feature engineering to model training to accelerate machine learning model development](/img/f6/311d5a4c70993df6291250d2025d3f.jpg)
[Meetup Preview] OpenMLDB+OneFlow: Link feature engineering to model training to accelerate machine learning model development

宁波大学NBU IT项目管理期末考试知识点整理
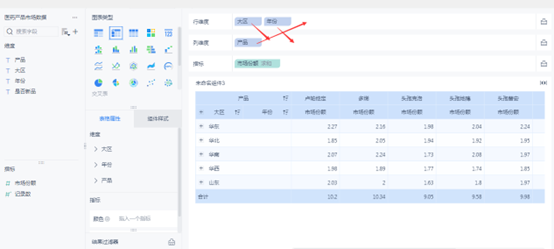
What is the difference between BI software in the domestic market?

第二届中国PWA开发者日

Kubernetes principle analysis and practical application manual, too complete

联邦学习:联邦场景下的多源知识图谱嵌入

【7.29】Code Source - 【Arrangement】【Stone Game II】【Cow and Snacks】【Minimum Number of Spawns】【Sequence】
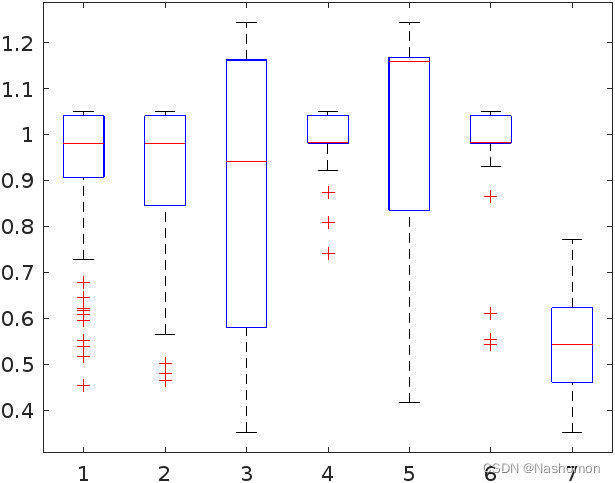
长得很怪的箱图
动态规划之线性dp(上)
随机推荐
Graham's Scan method for solving convex hull problems
2022年必读的12本机器学习书籍推荐
ML.NET related resources
多主复制的适用场景(1)-多IDC
ansible study notes 02
Dialogue with Zhuang Biaowei: The first lesson of open source
tensorflow2.0 cnn(layerwise)
研发过程中的文档管理与工具
Implementing click on the 3D model in RenderTexture in Unity
牛客网刷题(一)
Insert into data table to insert data
Mariabackup实现Mariadb 10.3的增量数据备份
Three aspects of Ali: How to solve the problem of MQ message loss, duplication and backlog?
基于Redis(SETNX)实现分布式锁,案例:解决高并发下的订单超卖,秒杀
Applicable scenario of multi-master replication (2) - client and collaborative editing that require offline operation
SringMVC中个常见的几个问题
最新神作!阿里巴巴刚出炉的面试参考指南(泰山版),我直接狂刷29天
牛客 HJ20 密码验证合格程序
智能垃圾桶(八)——红外对管传感器(树莓派pico)
After Effects 教程,如何在 After Effects 中调整过度曝光的快照?