Defense (greed), FBI tree (binary tree)

Defense

Title Description

Xiao Ming is playing a game recently . Interested in defense in the game .

We believe that the parameters that directly affect defense are " Defense performance ", Write it down as  d, And there are two defense values on the panel  A  and  B , And  d It's logarithmic ,A=2^d,B=3^d（ Note that the above formula holds at any time ）.

During the game , There may be some props that put the defense value  A  Add a value , There are other props that put defense value  BB  Add a value .

Now Xiao Ming has  n1​  Props increase  A  The value of and  n2​  Props increase  B  Value , The increase is known .

It is now known that  i  The second use of props is to increase  A  Or increase  B  Value , But the specific use of that prop is uncertain , Please find a way to use props with the smallest dictionary order , Make the final defense performance maximum .

The initial defense performance is  0, namely  d=0, therefore  A=B=1.

Input description

The first line of input contains two numbers n1,n2, The blank space to separate .

The second line n1 Number , Said to increase A The increase in the value of those props .

The third line n2 Number , Said to increase B The increase in the value of those props .

The fourth line has a length of n1+n2 String , from 0 and 1 form , Indicates the use order of props .0 Indicates that the use of A Worth of props ,1 Indicates that the use of B Worth of props . The input data ensures that there happens to be n1 individual 0,n2 individual 1 .

among , String length ≤2×10^6, Each increment entered does not exceed  2^30.

Output description

For each set of data , Output  n1​+n2​+1  That's ok .

front  n1​+n2​  Output the usage of props in order , If used, add A  Worth of props , Output  Ax ,x  Is the number of the item in this type of item （ from 1 Start ）. If used, add  B The value of the prop is output  Bx.

The last line outputs a capital letter  E .

The sample input

1 2 4 2 8 101 

Sample output

B2 A1 B1 E

  Ideas ：

First of all, read it several times to understand the meaning of the topic , Then use the sample data to further understand the meaning of the topic , Here's the picture

  Therefore, what we need to analyze is how to increase A,B To make d Value is the largest .

1. When continuously increasing A or B when , We use A As an example d=log2​(1+A1+A2+⋯), Therefore, it has nothing to do with the increase of contact .

2. When A or B When increasing alternately , We analyzed it with examples ,B Props from large to small are conducive to d An increase in ,A Props from small to large are conducive to d An increase in .

So we can code with greedy method

Yes Ai​  Sort the structure , First pair Ai​​ Sort by the amount of increase from small to large , Press the subscript again ( Dictionary order ) Sort .

Yes Bi​​ Sort the structure , First pair Bi​​ Sort by the amount of increase from large to small , Press the subscript again ( Dictionary order ) Sort .

Then, in the order required by the topic , Output Ai​  and Bi​.

The code is as follows ：

#include <bits/stdc++.h>
using namespace std;
struct nodea {  // A The props of 
    int id, w;  //id It's a prop ,w It's the increase of this prop 
}a[100005];
struct nodeb { // B The props of 
    int id, w;
}b[100005];
bool cmp1(nodea a, nodea b) {
    if (a.w != b.w) return a.w < b.w;    // First pair A Sort the increase of , From small to large 
    else return a.id < b.id;            // Then in dictionary order id Sort 
}
bool cmp2(nodeb a, nodeb b) {             // First pair B Sort the increase of , From big to small 
    if (a.w != b.w) return a.w > b.w;
    else return a.id < b.id;
}
int main() {
    int n1, n2;
    cin >> n1 >> n2;
    for (int i = 1; i <= n1; i++)  cin >> a[i].w, a[i].id = i;
    for (int i = 1; i <= n2; i++)  cin >> b[i].w, b[i].id = i;
    sort(a + 1, a + n1 + 1, cmp1);
    sort(b + 1, b + n2 + 1, cmp2);
    string s;
    cin >> s;
    int idx1 = 1, idx2 = 1;
    for (int i = 0; i < s.length(); i++) {
        if (s[i] == '1') {
            cout << "B";
            cout << b[idx1++].id << endl;
        }
        else {
            cout << "A";
            cout << a[idx2++].id << endl;
        }
    }
    cout << "E" << endl;
    return 0;
}

FBI Trees

Title Description

We can turn the “0” and “1” There are three types of strings ： whole “0” The string is called B strand , whole “1” The string is called I strand , Both contain “0” It also includes “1” The string of is called F strand .

FBI A tree is a binary tree , Its node types also include F node ,B Node sum I There are three kinds of nodes . By a length of  2^N  Of “01” strand S You can build a tree FBI Trees T, The construction of recursion is as follows ：

1. T The root node of is R, Its type and string S Same type of ;

2. Ruoshan S Is longer than 1, String S Separate from the middle , It is divided into equal length left and right substrings S1 and S2 ; From left sub string S1 structure R The left subtree T1, From the right sub string S2 structure R The right subtree T2.

Now let's give a length of  2^N  Of “01” strand , Please construct a FBI Trees , And output its post order traversal sequence .

Input description

The first line is an integer N（0≤N≤10）.

The second line is a length of  2^N  Of “01” strand .

Output description

Output a string , namely FBI The subsequent traversal sequence of the tree .

I/o sample

Example 1

Input

3
10001011

Output

IBFBBBFIBFIIIFF

  Ideas ：

The idea is simple , Just assign the leaf node as a character according to the rules  F、B、I, Their upper parent nodes are also assigned characters according to rules  F、B、I, We can use recursion to solve . Finally, use the post order traversal to print the binary tree . You can quickly understand the meaning of the question with the following sample diagram .

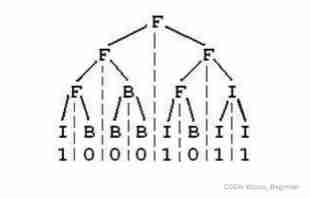
The code is as follows ： 

#include <bits/stdc++.h>
using namespace std;
char s[2000], tree[280000]; //tree[] Full binary tree 

void build_FBI(int k, int left, int right) {
    if (left == right) {      // Reach the leaf node 
        if (s[right] == '1') tree[k] = 'I';
        else tree[k] = 'B';
        return;
    }
    int mid = (left + right) / 2;      // Split in two 
    build_FBI(2 * k, left, mid);     // Recursive left half 
    build_FBI(2 * k + 1, mid + 1, right); // Recursive right half 

    if (tree[2 * k] == 'B' && tree[2 * k + 1] == 'B') // Both left and right sons B
        tree[k] = 'B';
    else if (tree[2 * k] == 'I' && tree[2 * k + 1] == 'I') // Both left and right sons I
        tree[k] = 'I';
    else tree[k] = 'F';
}
void postorder(int v) {   // After the sequence traversal 
    if (tree[2 * v])         postorder(2 * v);
    if (tree[2 * v + 1])         postorder(2 * v + 1);
    printf("%c", tree[v]);
}
int main() {
    int n;        scanf("%d", &n);
    scanf("%s", s + 1);
    build_FBI(1, 1, strlen(s + 1));
    postorder(1);
}

ly