当前位置:网站首页>js中小数四则运算精度问题原因及解决办法
js中小数四则运算精度问题原因及解决办法
2022-08-04 22:32:00 【hzxOnlineOk】
先带着问题看如下2张截图(一脸懵逼)

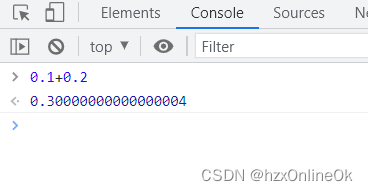
本篇文章主要参考自该博主:https://www.cnblogs.com/zm-blogs/p/12909096.html
js number类型
JS 数字类型只有number类型,number类型相当于其他强类型语言中的double类型(双精度浮点型),不区分浮点型和整数型。
number类型不同进制
number 有四种进制表示方法,十进制,二进制,八进制和十六进制
二进制: 0B或者0b (数字0和字母B或者小写字母b) ,后接1或者0表示二进制数八进制: es5下禁止表示八进制数会自动转化为十进制数,es6用0o ,后接小于8的数字表示八进制十六进制: 以0x或者0X开头,后接0-9数字和a-e五个英文字母十进制:默认直接输入0-9都是十进制数
二进制和十进制互转请参考:https://zhuanlan.zhihu.com/p/75291280
小数,浮点数,及小数运算
由于Js的所有数字类型都是双精度浮点型(64位)采用 IEEE754 标准
64位二进制数表示一个number数字
其中 64位 = 1位符号位 + 11位指数位 + 52位小数位
符号位:用来表示数字的正负,-1^符号位数值,0为正数,1为负数
指数位:一般都用科学计数法表示数值大小,但是这里一般都是2进制的科学计数法,表示2的多少次方
小数位:科学计数法前面的数值,IEEE745标准,默认所有的该数值都转为1.xxxxx这种格式,优点是可以省略一位小数位,可以存储更多的数字内容,缺点是丢失精度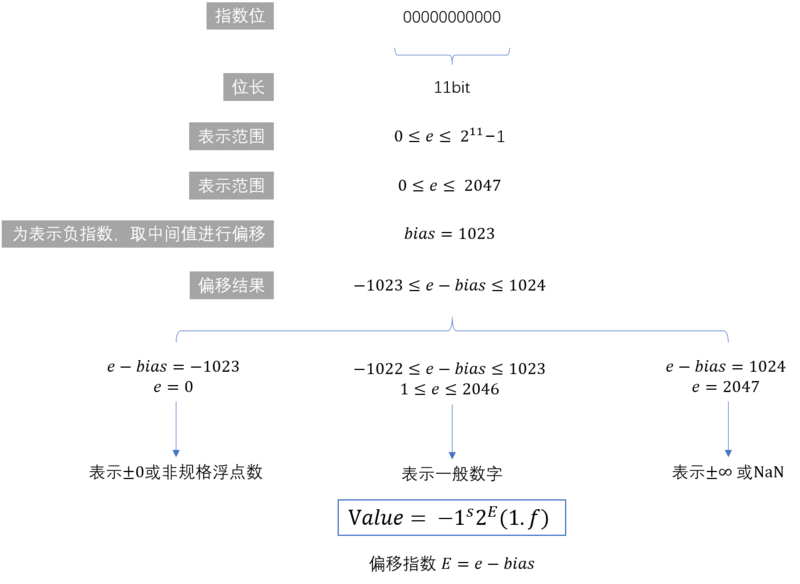
浮点数的运算精度丢失问题就是因为,浮点数转化为该标准的二进制的过程中出现的丢失
整数转二进制
好理解,除二取余法,3(10进制)转二进制
3 / 2 = 1 // 余1
1 / 2 = 0 // 余1
倒着从下往上看 3(十进制) = 11(二进制),二进制转10进制,则是 11 = 1 * 2^0 + 1 * 2^1 = 1 + 2 = 3
整数10转2的口诀是除2取余,从下往上
小数10转2的口诀是乘2取整数,小数继续乘2,继续取整数,直到小数部分为0,最后的结果为整数补0.从上往下看
问题来了,小数如何转二进制!!
由于也需要转化为指数形式,例如 1/2 = 1 * 2^-1, 1/4 = 1 * 2^-2,所以小数的转化二进制过程是通过判断小数是不是满 1/2,1/4,1/8(因为这些数才能乘2后小数部位取余为0)以此类推,换成数学公式就是,乘二取整法
0.125的二进制
0.125 * 2 = 0.25 ====== 取出整数部分0
0.25 * 2 = 0.5 ====== 取出整数部分0
0.5 * 2 = 1.0 ====== 取出整数部分1
所以0.125转化成二进制是:0.001
0.1的二进制
0.1*2=0.2======取出整数部分0
0.2*2=0.4======取出整数部分0
0.4*2=0.8======取出整数部分0
0.8*2=1.6======取出整数部分1
0.6*2=1.2======取出整数部分1
0.2*2=0.4======取出整数部分0
0.4*2=0.8======取出整数部分0
0.8*2=1.6======取出整数部分1
0.6*2=1.2======取出整数部分1
接下来会无限循环
0.2*2=0.4======取出整数部分0
0.4*2=0.8======取出整数部分0
0.8*2=1.6======取出整数部分1
0.6*2=1.2======取出整数部分1
所以0.1转化成二进制是:0.0001 1001 1001 1001…(无限循环)
0.1 => 0.0001 1001 1001 1001…(无限循环)
同理0.2的二进制是0.0011 0011 0011 0011…(无限循环)
OK ,转化为二进制之后,开始准备运算
计算机中的数字都是以二进制存储的,二进制浮点数表示法并不能精确的表示类似0.1这样 的简单的数字
如果要计算 0.1 + 0.2 的结果,计算机会先把 0.1 和 0.2 分别转化成二进制,然后相加,最后再把相加得到的结果转为十进制
但有一些浮点数在转化为二进制时,会出现无限循环 。比如, 十进制的 0.1 转化为二进制,会得到如下结果:
0.1 => 0.0001 1001 1001 1001…(无限循环)
0.2 => 0.0011 0011 0011 0011…(无限循环)
而存储结构中的尾数部分最多只能表示 53 位。为了能表示 0.1,只能模仿十进制进行四舍五入了,但二进制只有 0 和 1 , 于是变为 0 舍 1 入 。 因此,0.1 在计算机里的二进制表示形式如下:
0.1 => 0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 101
0.2 => 0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 001
用标准计数法表示如下:
0.1 => (−1)0 × 2^4 × (1.1001100110011001100110011001100110011001100110011010)2
0.2 => (−1)0 × 2^3 × (1.1001100110011001100110011001100110011001100110011010)2
在计算浮点数相加时,需要先进行 “对位”,将较小的指数化为较大的指数,并将小数部分相应右移:
最终,“0.1 + 0.2” 在计算机里的计算过程如下:

经过上面的计算过程,0.1 + 0.2 得到的结果也可以表示为:
(−1)0 × 2−2 × (1.0011001100110011001100110011001100110011001100110100)2=>.0.30000000000000004
通过 JS 将这个二进制结果转化为十进制表示:
(-1)0 * 2-2 * (0b10011001100110011001100110011001100110011001100110100 * 2**-52); //0.30000000000000004
console.log(0.1 + 0.2) ; // 0.30000000000000004
这是一个典型的精度丢失案例,从上面的计算过程可以看出,0.1 和 0.2 在转换为二进制时就发生了一次精度丢失,而对于计算后的二进制又有一次精度丢失 。因此,得到的结果是不准确的。
但是问题是:几乎所有的编程语言浮点数都是都采用IEEE浮点数算术标准~
JAVASCRIPT中的解决办法
(1)原生方法类
因为浮点数转换的时候小数乘二取整会有无限循环的情况,但是整数除二取余是不会的,所以整数部分不会出现精度丢失问题方案1:将小数转化为整数进行运算
实现思想:先将小数转化为字符串,判断小数部分位数,并且将运算两边小数同时乘以10最大小数位数,再将最后结果除以10最大小数位数
因为小数精度过高的情况下可能出现无限循环,出现截断或者进位等情况方案2:限制精度,只保留小数部分位数,减小精度出现的误差问题
方法:Number.toFixed()
代码:
console.log((0.1 + 0.2).toFixed(12) == 0.3)
// true
console.log((0.1 + 0.2).toFixed(12))
// 0.300000000000
console.log((2.4/0.8).toFixed(12))
// 3.000000000000
注意:toFixed之后会转换为字符串格式,可以再使用parseFloat转换为小数 parseFloat((a+b).toFixed(2))
(2)第三方封装类库math库
统一配置math.js
math.config({
number: 'BigNumber',
// 'number' (default),
precision: 20
});
// 转换数字类型
var temp = math.bignumber(a) * math.bignumber(b)
// 提取数字类型,不然会是一个math对象
var result = math.number(temp)
bignumber、big、decimal等
将js原生number类型转为bignumber,big,decimal等封装类型,(decimal是8421 BCD编码,bignumber是支持高精度的数据类型,实现原理则大概是用类数组存储数据位,保持精度的可靠性)
边栏推荐
- 边缘检测——(纯享版)
- # #ifndef/#define/#endif使用详解
- Oracle增加表空间解决ORACLE ORA-01653: unable to extend table报错
- 【2020】【论文笔记】超表面:多功能和可编程——
- synchronized和ReentrantLock都很丝滑,因为他们都是可重入锁,一个线程多次拿锁也不会死锁,我们需要可重入
- Redis understanding
- JVM memory configuration parameter GC log
- 重新配置chrome中ffmpeg插件
- OC-拷贝
- 历史上的今天:PHP公开发布;iPhone 4 问世;万维网之父诞生
猜你喜欢
2022强网杯web(部分)
How to make a video gif?Try this video making gif artifact
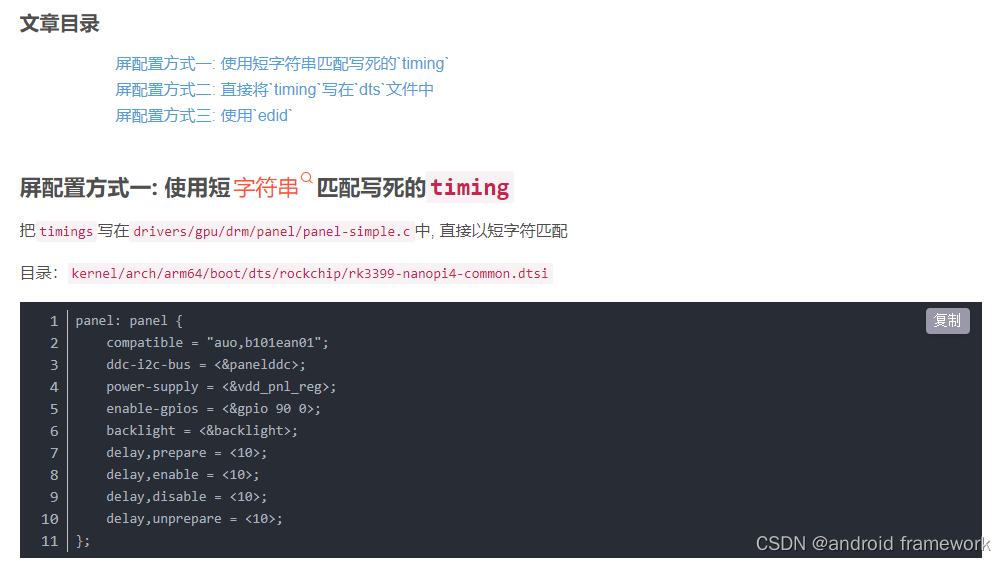
Several ways for rk3399 to drive screen parameters

湖仓一体电商项目(五):内网穿透工具-网云穿

开源一夏 | 云服务器ECS安装Mysql、JDK、RocketMQ

赶紧进来!!!教你C语言实现扫雷小游戏(文章最后有源码!!!)

各行各业都受到重创,游戏行业却如火如荼,如何加入游戏模型师职业
软件测试外包公司怎么样?有什么好处和坏处?为什么没人去?

Debian防火墙的开关以及状态

中国的顶级黑客在国际上是一个什么样的水平?
随机推荐
# #ifndef/#define/#endif使用详解
【游戏建模模型制作全流程】ZBrush蜥蜴模型雕刻教程
【论文笔记KDD2021】MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
DREAMWEAVER8 部分问题解决方案
【3D建模制作技巧分享】ZBrush模型制作流程:地精
rk3399 驱动屏参的几种方式
The Record of Reminding myself
软件测试外包公司怎么样?有什么好处和坏处?为什么没人去?
今天是七夕,来看看程序员的土味情话。
Milvus configuration related
Operations on std::vector
智慧养老整体解决方案
puzzle(022.1)黑白迭代
【游戏建模模型制作全流程】使用ZBrush制作骷髅王
JVM内存配置参数GC日志
Why is MySQL query slow?
基于事实的结果
现在学习次世代3D游戏建模还能找到高薪好工作吗
3D建模师为了让甲方爸爸过稿,还可以这么做,就是在赚血汗钱啊
idea 仓库地址连接不上问题
