当前位置:网站首页>【论文笔记KDD2021】MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
【论文笔记KDD2021】MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
2022-08-04 22:03:00 【山顶夕景】
学习总结
零、论文简介
论文题目:MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
论文链接:http://keg.cs.tsinghua.edu.cn/jietang/publications/KDD21-Huang-et-al-MixGCF.pdf
论文代码:https://github.com/huangtinglin/MixGCF
论文作者:Tinglin Huang,唐杰老师等人
一、Introduction
导言:GNN被广泛应用于embedding的生成场景,对user和item分别进行embedding化,使用双塔模型;类似像Graphsage、PinSage、LightGCN等算法也有被应用在工业界的推荐系统上,但是GNN的负采样技术还有待研究,过去大多数算法是从真实的数据中选取负样本,而忽略了embedding的信息,而MixGCF是经过数据增强、聚合的方法获取负样本及其表示。NGCF和LightGCN在使用MixGCF后,在NDCG指标上分别提高了26%和22%。
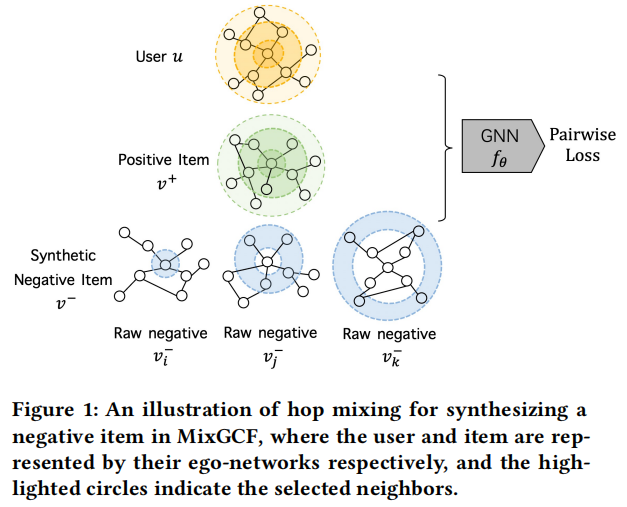
1.1 聚合 Aggregation
聚合过程: e u ( l + 1 ) = ∑ i ∈ N u 1 ∣ N u ∣ ∣ N i ∣ e i ( l ) , e v ( l + 1 ) = ∑ j ∈ N v 1 ∣ N v ∥ N j ∣ e j ( l ) \mathbf{e}_{u}^{(l+1)}=\sum_{i \in N_{u}} \frac{1}{\sqrt{\left|N_{u}\right|\left|N_{i}\right|}} \mathbf{e}_{i}^{(l)}, \mathbf{e}_{v}^{(l+1)}=\sum_{j \in N_{v}} \frac{1}{\sqrt{\left|N_{v} \| N_{j}\right|}} \mathbf{e}_{j}^{(l)} eu(l+1)=i∈Nu∑∣Nu∣∣Ni∣1ei(l),ev(l+1)=j∈Nv∑∣Nv∥Nj∣1ej(l)
1.2 池化过程
池化过程: e u ∗ = ∑ l = 0 L λ l e u ( l ) , e v ∗ = ∑ l = 0 L λ l e v ( l ) \mathbf{e}_{u}^{*}=\sum_{l=0}^{L} \lambda_{l} \mathbf{e}_{u}^{(l)}, \mathbf{e}_{v}^{*}=\sum_{l=0}^{L} \lambda_{l} \mathbf{e}_{v}^{(l)} eu∗=l=0∑Lλleu(l),ev∗=l=0∑Lλlev(l)
1.3 负采样优化
一般LTR任务的损失函数是BPR loss: max ∏ v + , v − ∼ f S ( u ) P u ( v + > v − ∣ Θ ) \max \prod_{v^{+}, v^{-} \sim f_{S}(u)} P_{u}\left(v^{+}>v^{-} \mid \Theta\right) maxv+,v−∼fS(u)∏Pu(v+>v−∣Θ)
其中参数:
- v + v^{+} v+和 v − v^{}- v−分别表示positive items和negative items
- P u ( a > b ) P_{u}(a>b) Pu(a>b)表示用户u,相比于item b来说,更加偏爱于item a
- f S ( u ) f_{S}(u) fS(u)是negative sampling的分布,很多推荐算法(如LightGCN、NCF、BPR、NGCF等算法)都是将negative sample服从于uniform均匀分布( f S ( u ) = f uniform ( u ) f_{S}(u)=f_{\text {uniform }}(u) fS(u)=funiform (u))
1.4 负采样问题
- 经典的BPR loss栗子。
- 负采样一般使用uniform distribution,为了改进GNN的负采样:
- PinSage根据PageRank的得分进行负采样;
- MCN考虑正负样本之间的结构相关性,重新涉及额了正负样本的分布;
- 但是这些算法只是主要在discrete graph space中负采样,而忽略了GNN在embedding空间中独特的邻居聚合过程。
- MixGCF受数据增强和metric learning的思想而提出,进行hard负样本的生成。
二、MixGCF算法
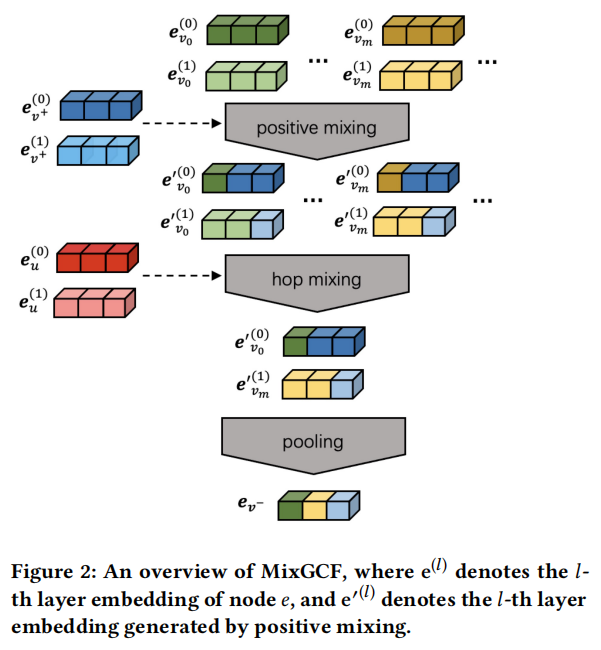
2.1 positive mixing
positive mixing的操作: e v m ′ ( l ) = α ( l ) e v + ( l ) + ( 1 − α ( l ) ) e v m ( l ) , α ( l ) ∈ ( 0 , 1 ) \mathbf{e}_{v_{m}}^{\prime(l)}=\alpha^{(l)} \mathbf{e}_{v^{+}}^{(l)}+\left(1-\alpha^{(l)}\right) \mathbf{e}_{v_{m}}^{(l)}, \alpha^{(l)} \in(0,1) evm′(l)=α(l)ev+(l)+(1−α(l))evm(l),α(l)∈(0,1)
其中参数:
- α ( l ) \alpha^{(l)} α(l)是每一个hop的均匀采样的mixing因子;
- mixup的mixing因子是从beta分布 Beta ( β , β ) \operatorname{Beta}(\beta, \beta) Beta(β,β)中采样而来的,对模型的泛化能力有很大影响;
- 为了缓解上面提到的这个影响,positive mixing中的mixing因子 α ( l ) \alpha^{(l)} α(l)统一从(0, 1)分布中进行采样;
- E ′ \mathcal{E}^{\prime} E′是候选negatives M增强后的embedding集合。
positive mixing增强negatives通过以下两种方式:
1)把positive information注射到negative samples,这样有助于强制优化算法更努力、更狠的利用决策边界。
2)用mixing因子把随机不确定性引入它们之中。
2.2 Hop Mixing

2.3 optimization with MixGCF
L B P R = ∑ ( u , v + ) ∈ O + e v − ∼ f M i x G C F ( u , v + ) ln σ ( e u ⋅ e v − − e u ⋅ e v + ) \mathcal{L}_{\mathrm{BPR}}=\sum_{\substack{\left(u, v^{+}\right) \in O^{+} \\ \mathbf{e}_{v^{-}} \sim f_{\mathrm{MixGCF}}\left(u, v^{+}\right)}} \ln \sigma\left(\mathbf{e}_{u} \cdot \mathbf{e}_{v^{-}}-\mathbf{e}_{u} \cdot \mathbf{e}_{v^{+}}\right) LBPR=(u,v+)∈O+ev−∼fMixGCF(u,v+)∑lnσ(eu⋅ev−−eu⋅ev+)
2.4 关于MixGCF的相关讨论
2.5 时间复杂度
三、实验环节
3.1 experimental settings
(1)评估指标
(2)推荐算法模型
(3)Baselines
(4)超参数设置
3.2 Performance comparison
实验结果对比: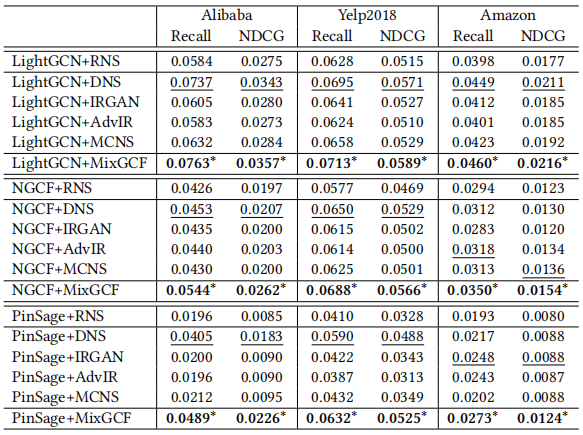
(1)running time
(2)running time
四、相关工作
4.1 基于GNN的推荐算法
- PinSage、GC-MC、NGCF、LightGCN
- 利用side info:社交网络、知识图谱 …
4.2 推荐系统中的负采样
- Static Sampler 从一个固定的分布中进行负采样
- 均匀分布、流行度 指数 3/4
- GAN-based Sampler 基于生成对抗网络进行负采样
- IRGAN、KBGAN、AdvIR
- Hard Negative Sampler 为当前的用户自适应地选择 hardest 负样本
- DNS
- Graph-based Sampler 根据图信息进行负采样
- MCNS、KGPolicy、PinSage(基于Personalized PageRank)
Reference
[1] http://keg.cs.tsinghua.edu.cn/jietang/publications/KDD21-Huang-et-al-MixGCF.pdf
[2] https://huangtinglin.github.io/experience/
[3] 贝叶斯个性化排序算法BPR
边栏推荐
猜你喜欢

【社媒营销】WhatsApp Business API:您需要知道的一切
七夕,当爱神丘比特遇上牛郎和织女
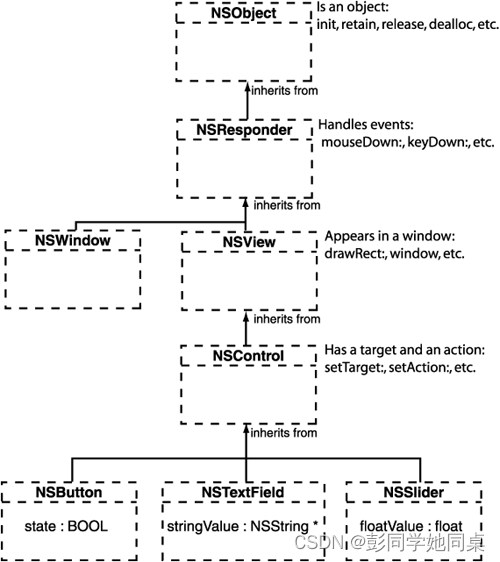
Cocoa Application-基础
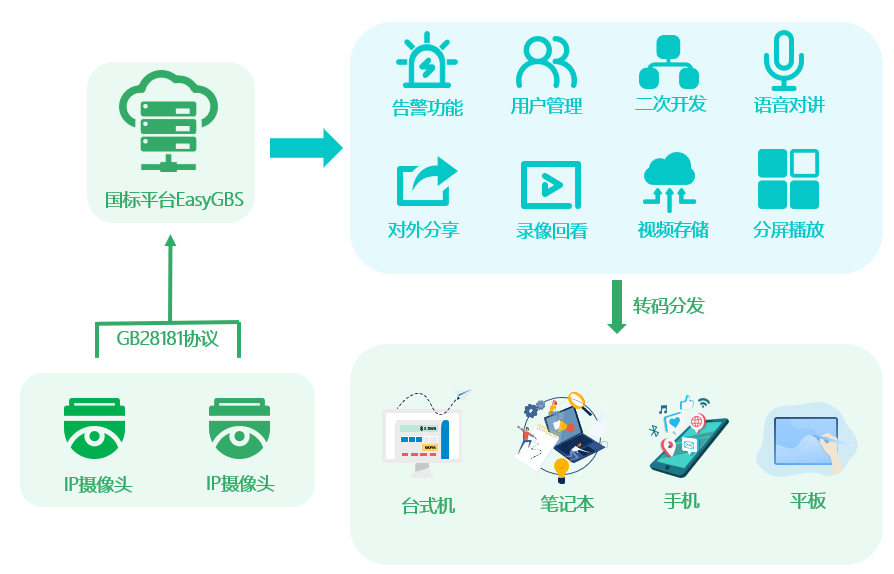
How to solve the problem that the alarm information cannot be transmitted after EasyGBS is connected to the latest version of Hikvision camera?
Unknown point cloud structure file conversion requirements
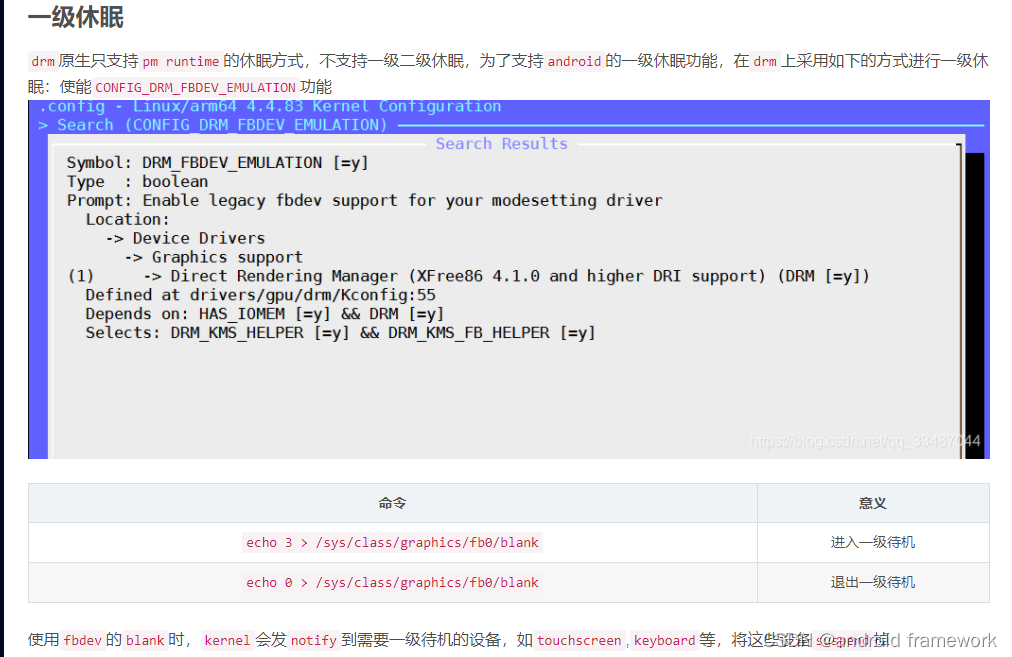
rk3399-9.0一级二级休眠
【QT】回调函数的实现
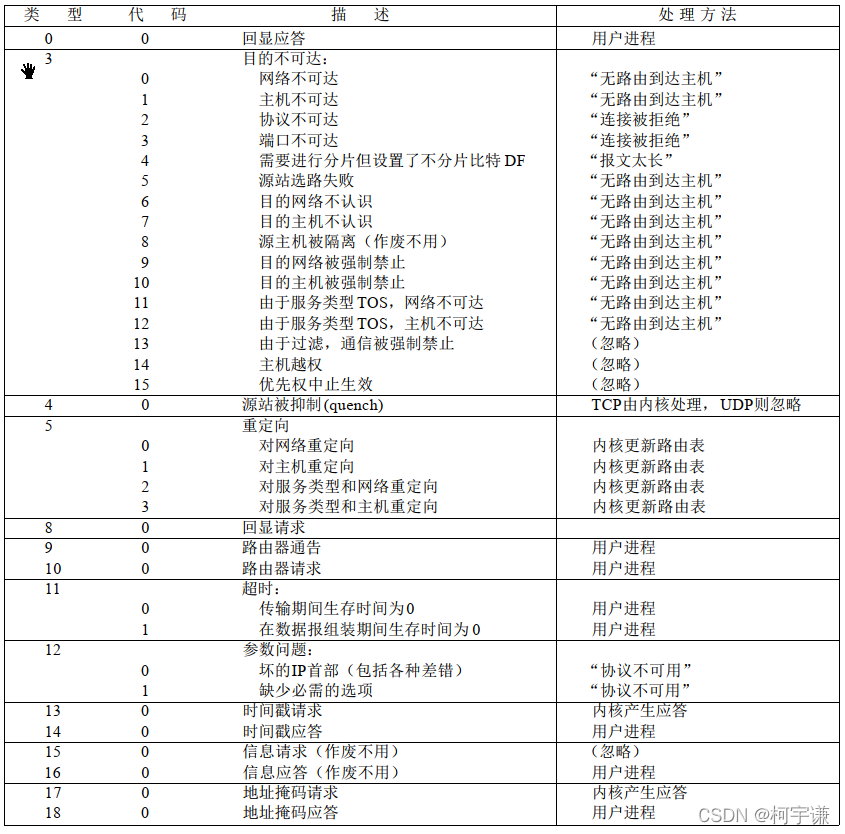
【TCP/IP 五 ICMP】

双非读者,一举拿下阿里、字节、美团、京东、虾皮offer

Cocoa Application-test
随机推荐
Yolov7:Trainable bag-of-freebies sets new state-of-the-art for real-time objectdetectors
单片机原理[一] 学好单片机必会的五张图
Unknown point cloud structure file conversion requirements
NFT宝典:你需要知道NFT的术语和定义
CountDownLatch使用及原理
rk3399-9.0 first-level and second-level dormancy
3D激光SLAM:LeGO-LOAM---两步优化的帧间里程计及代码分析
The use and principle of CountDownLatch
AI/ML无线通信
【QT】回调函数的实现
Is the International Project Manager PMP certificate worth taking?
Ramnit感染型病毒分析与处置
打卡第 1 天:正则表达式学习总结
Flutter 实现背景图片毛玻璃效果
puzzle(022.1)黑白迭代
Win11如何开启Telnet客户端?
关于el-table列表渲染
数字重塑客观世界,全空间GIS发展正当其时
【线性代数02】AX=b的2种解释和矩阵乘法的5种视角
热力学相关的两个定律