当前位置:网站首页>Detailed explanation of common examples of dynamic programming
Detailed explanation of common examples of dynamic programming
2022-08-02 22:02:00 【Big dream who realizes i】
活动地址:CSDN21天学习挑战赛
什么是动态规划
首先很多人问,何为动态规划?动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程.通俗一点动态规划就是从下往上(从前向后)阶梯型求解数值.
那么动态规划和递归有什么区别和联系?
总的来说动态规划从前向后,递归从后向前,两者策略不同,并且一般动态规划效率高于递归.
不过都要考虑初始状态,上下层数据之间的联系.很多时候用动态规划能解决的问题,用递归也能解决不过很多时候效率不高可能会用到记忆化搜索.
不太明白?
就拿求解斐波那契额数列来说,如果直接用递归不优化,那么复杂度太多会进行很多重复的计算.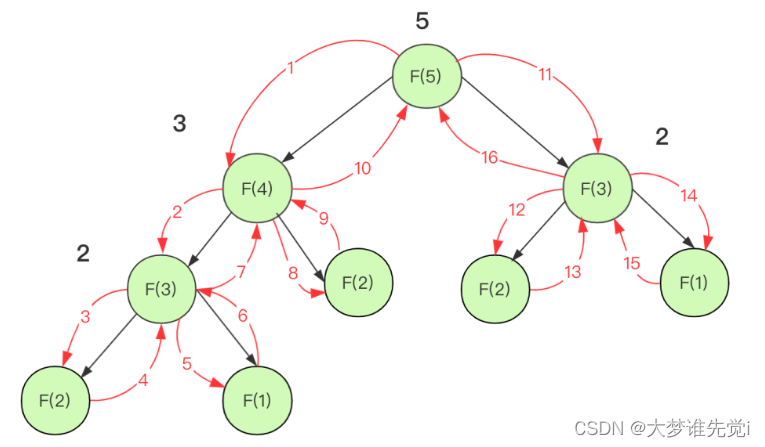
但是利用记忆化你可以理解为一层缓存,将求过的值存下来下次再遇到就直接使用就可以了.
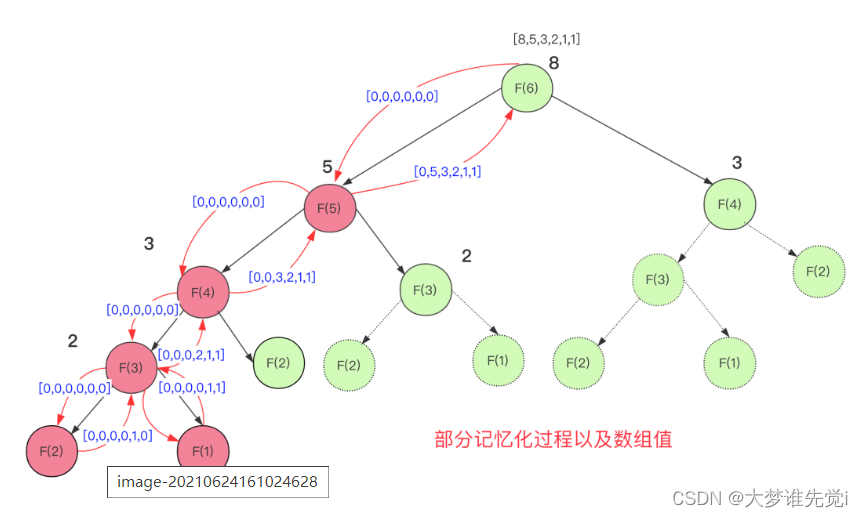
实现记忆化搜索求斐波那契代码为:
static long F(int n,long record[])
{
if(n==1||n==2) {
return 1;}
if(record[n]>0)
return record[n];
else
record[n]=F(n-1,record)+F(n-2,record);
return record[n];
}
public static void main(String[] args) {
int n=6;
long[] record = new long[n+1];
System.out.println(F(n,record));
}
而动态规划的方式你可以从前往后逻辑处理,从第三个开始每个dp都是前两个dp之和.
public int fib(int n) {
int dp[]=new int[n+1];
dp[0]=0;
dp[1]=1;
for(int i=2;i<n+1;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
当然动态规划也能有很多空间优化,有些只用一次的值,你可以用一些变量去替代.有些二维数组很大也可以用一维数组交替替代.当然动态规划专题很大,有很多比如树形dp、状压dp、背包问题等等经常出现在竞赛中,能力有限这里就将一些出现笔试高频的动态规划!
连续子数组最大和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和.
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6.
dp的方法就是O(n)的方法.如果dp[i]表示以第i个结尾的最大序列和,而这个dp的状态方程为:
dp[0]=a[0]
dp[i]=max(dp[i-1]+a[i],a[i])
也不难解释,如果以前一个为截至的最大子序列和大于0,那么就连接本个元素,否则本个元素就自立门户.
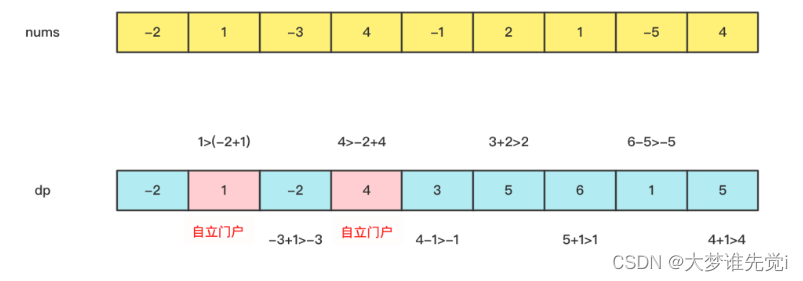
实现代码为:
public int maxSubArray(int[] nums) {
int dp[]=new int[nums.length];
int max=nums[0];
dp[0]=nums[0];
for(int i=1;i<nums.length;i++)
{
dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
if(dp[i]>max)
max=dp[i];
}
return max;
}
连续子数组最大乘积
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积.
示例 :
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6
.
连续子数组的最大乘积,这也是一道经典的动态规划问题,但是和普通动态规划又有点小不同.
如果数据中都是非负数,对于连续数组的最大乘积,那样处理起来和前面连续子数组最大和处理起来有些相似,要么和前面的叠乘,要么自立门户.
dp[0]=nums[0]
dp[i]=max(dp[i-1]*a[i],a[i])
但是这里面的数据会出现负数,乘以一个负数它可能从最大变成最小,并且还有负负得正就又可能变成最大了.
这时候该怎么考虑呢?
容易,我们开两个dp,一个dpmax[]记录乘积的最大值,一个dpmin[]记录乘积的最小值.然后每次都更新dpmax和dpmin不管当前值是正数还是负数.这样通过这两个数组就可以记录乘积的绝对值最大.
动态方程也很容易
dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
看一个过程就能理解明白,dpmin就是起到中间过度的作用,Record some possible negative values for backup.结果还是dpmax中的值.
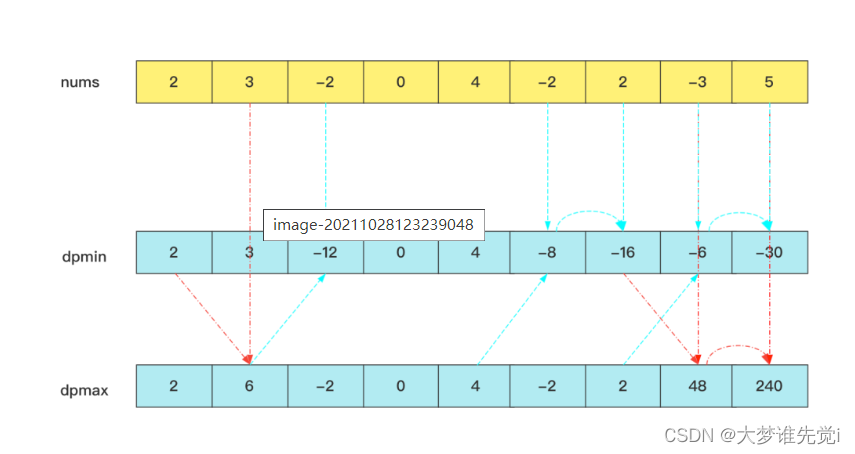
最长递增子序列
最长递增子序列,也称为LIS,是出现非常高频的动态规划算法之一.这里对应力扣300
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度.
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序.例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列.
输入:nums = [0,1,0,3,2,3]
输出:4
解释:最长递增子序列是 [0,1,2,3],因此长度为 4 .
对于最长递增子序列,如果不考虑动态规划的方法,使用暴力枚举其实还是比较麻烦的,因为你不知道遇到比前面元素大的是否要递增.
比如 1 10 3 11 4 5,这个序列不能选取1 10 11而1 3 4 5才是最大的,所以暴力枚举所有情况的时间复杂度还是非常高的.
如果我们采取动态规划的方法,创建的dp[]数组,dp[i]表示以nums[i]结尾的最长递增子序列,而dp[i]的求解方式就是枚举i号前面的元素和对应结尾的最长子序列,找到一个元素值小于nums[i]并且递增序列最长,这样的时间复杂度为O(n2).
状态转移方程为:
dp[i]=max(dp[j])+1, 其中0≤j<i且num[j]<num[i]
具体流程为:
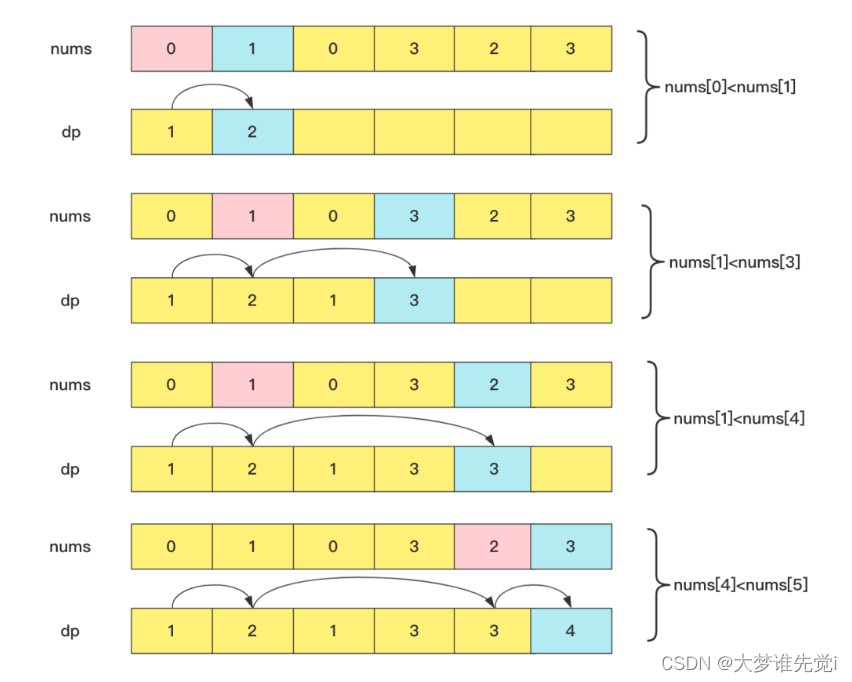
实现代码为:
class Solution {
public int lengthOfLIS(int[] nums) {
int dp[]=new int[nums.length];
int maxLen=1;
dp[0]=1;
for(int i=1;i<nums.length;i++){
int max=0;//统计前面 末尾数字比自己小 最长递增子串
for(int j=0;j<i;j++){
//枚举
//结尾数字小于当前数字 并且长度大于记录的最长
if(nums[j]<nums[i]&&dp[j]>max){
max=dp[j];
}
}
dp[i]=max+1;//前面最长 加上自己
if(maxLen<dp[i])
maxLen=dp[i];
}
return maxLen;
}
}
最长公共子序列
最长公共子序列也成为LCS.出现频率非常高!
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度.如果不存在 公共子序列 ,返回 0 .
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串.
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列.
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列.
拿b c d d e和 a c e e d e举例,其的公共子串为c d e.如果使用暴力,复杂度太高会直接超时,就需要使用动态规划.两个字符串匹配,我们设立二维dp[][]数组,dp[i][j]表示text1串第i个结尾,text2串第jlength of the longest common substring ending in .
这里核心就是要搞懂状态转移,分析dp[i][j]的转换情况,当到达i,j时候:
如果text1[i]==text2[j],因为两个元素都在最末尾的位置,所以一定可以匹配成功,换句话说,这个位置的邻居dp值不可能大于他(最多相等).所以这个时候就是dp[i][j]=dp[i-1][j-1] +1;
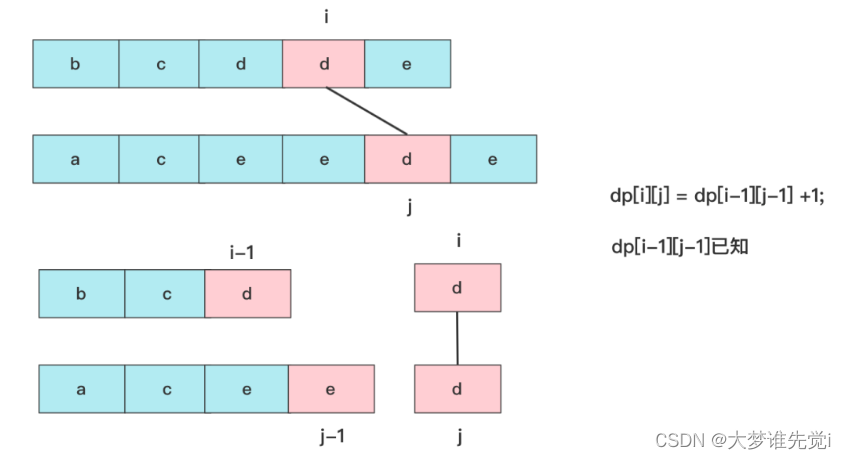
如果text1[i]!=text2[j],就有两种可能性,我们知道的邻居有dp[i-1][j],dp[i][j-1],很多人还会想到dp[i-1][j-1]这个一定比前两个小于等于,Because it's the first two sub-ranges.!所以这时就相当于末尾匹配不成,就要看看邻居能匹配的最大值啦,此时dp[i][j]=max(dp[i][j-1],dp[i-1][j]).
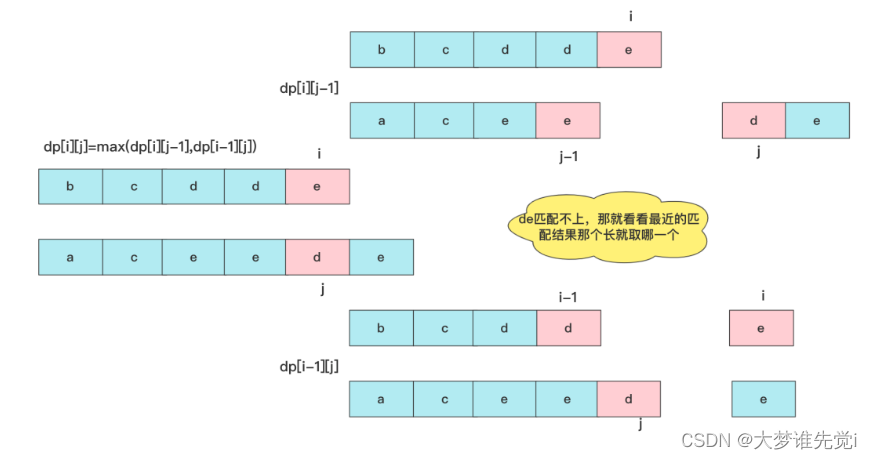
所以整个状态转移方程为:
dp[i][j] = dp[i-1][j-1] + 1 //text1[i]==text2[j]时
dp[i][j] = max(dp[i][j-1],dp[i-1][j]) //text1[i]!=text2[j]时
实现代码为:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
char ch1[]=text1.toCharArray();
char ch2[]=text2.toCharArray();
int dp[][]=new int[ch1.length+1][ch2.length+1];
for(int i=0;i<ch1.length;i++)
{
for(int j=0;j<ch2.length;j++)
{
if(ch1[i]==ch2[j])
{
dp[i+1][j+1]=dp[i][j]+1;
}
else
dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j]);
}
}
return dp[ch1.length][ch2.length];
}
}
最长公共子串
给定两个字符串str1和str2,输出两个字符串的最长公共子串.
例如 abceef 和a2b2cee3f的最长公共子串就是cee.公共子串是两个串中最长连续的相同部分.
如何分析呢? 和上面最长公共子序列的分析方式相似,要进行动态规划匹配,并且逻辑上处理更简单,只要当前i,j不匹配那么dp值就为0,如果可以匹配那么就变成dp[i-1][j-1] + 1
核心的状态转移方程为:
dp[i][j] = dp[i-1][j-1] + 1 //text1[i]==text2[j]时
dp[i][j] = 0 //text1[i]!=text2[j]时
这里代码和上面很相似就不写啦,但是有个问题有的会让你输出最长字符串之类,你要记得用一些变量存储值.
不同子序列
不同子序列也会出现,并且有些难度,You can take a look at the analysis of the different subsequence problems in the previous article.
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数.
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串.(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
示例 :
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案.
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^
分析:
这个问题其实就是上面有几个pat的变形拓展,其基本思想其实是一致的,上面那题问的是有几个pat,固定、且很短.但这里面t串的长度不固定,所以处理上就要使用数组来处理而不能直接if else.
这题的思路肯定也是动态规划dp了,dp[j]的意思就是t串中[0,j-1]长字符在s中能够匹配的数量(当然这个值从前往后是动态变化的),数组大小为dp[t.length+1].在遍历s串的每一个元素都要和t串中所有元素进行对比看看是否相等,如果s串枚举到的这个串和t串中的第j个相等.那么dp[j+1]+=dp[j].你可能会问为啥是dp[j+1],因为第一个元素匹配到需要将数量+1,而这里为了避免这样的判断我们将dp[0]=1,这样t串的每个元素都能正常的操作.
但是有一点需要注意的就是在遍历s串中第i个字母的时候,遍历t串比较不能从左向右而必须从右向左.因为在遍历s串的第i个字符在枚举dp数组时候要求此刻数据是相对静止的叠加(即同一层次不能产生影响),而从左往右进行遇到相同字符会对后面的值产生影响.区别的话可以参考下图这个例子:
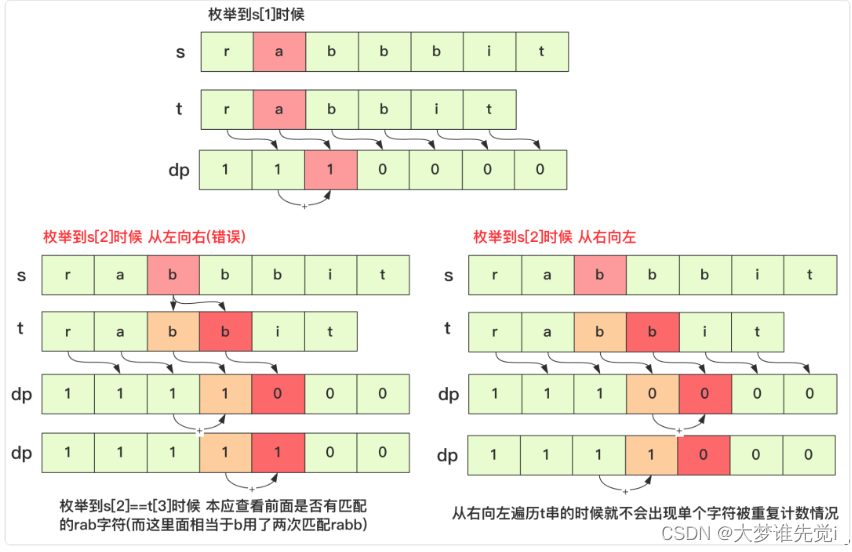
实现的代码为:
class Solution {
public int numDistinct(String s, String t) {
char s1[]=s.toCharArray();
char t1[]=t.toCharArray();
int dp[]=new int[t1.length+1];
dp[0]=1;//用来叠加
for(int i=0;i<s1.length;i++)
{
for(int j=t1.length-1;j>=0;j--)
{
if(t1[j]==s1[i])
{
dp[j+1]+=dp[j];
}
}
}
return dp[t1.length];
}
}
结语
至此,简单的动态规划算是分享完了.
大部分简单动态规划还是有套路的,你看到一些数组问题、字符串问题很有可能就暗藏动态规划.动态规划的套路跟递归有点点相似,主要是找到状态转移方程,有时候考虑问题不能一步想的太多(想太多可能就把自己绕进去了),而动态规划就是要大家对数值上下转换计算需要了解其中关系.
边栏推荐
猜你喜欢
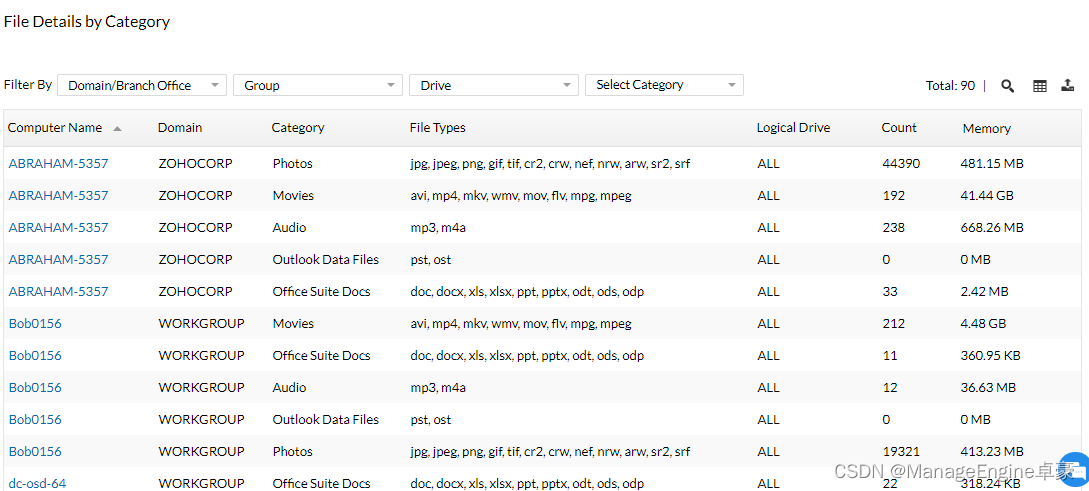
有什么好用的IT资产管理软件
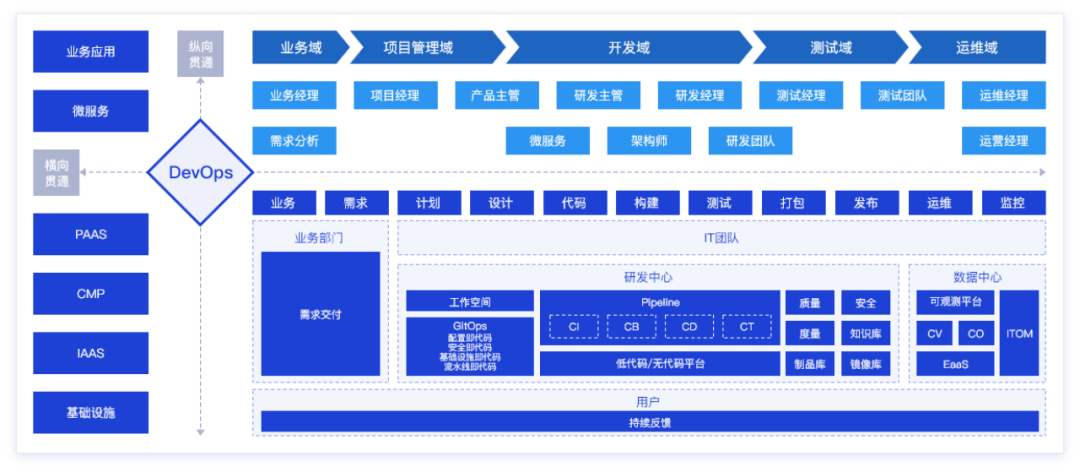
Boyun Selected as Gartner China DevOps Representative Vendor
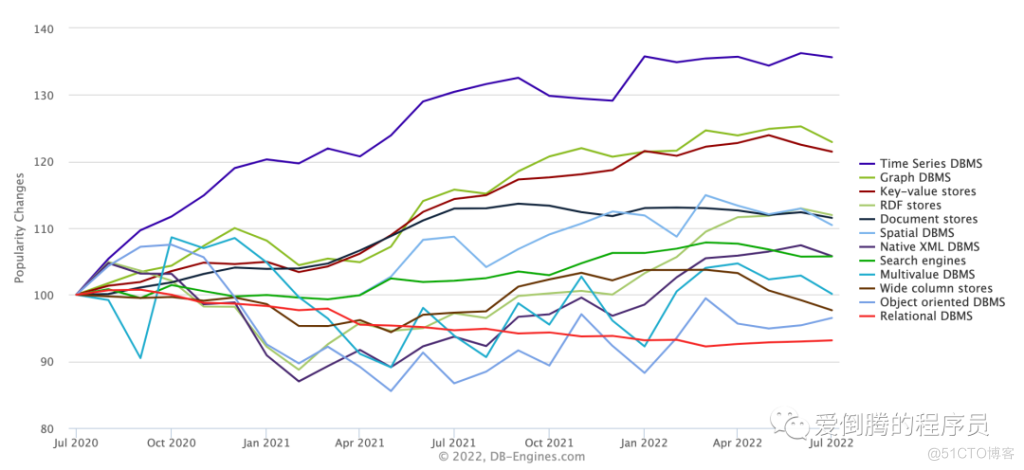
研发了 5 年的时序数据库,到底要解决什么问题?

手机银行体验性测试:如何获取用户真实感受

【动态规划专项训练】基础篇
Jupyter Notebook(Anaconda)——两个环境分别修改默认打开目录(深度学习第一周番外篇)
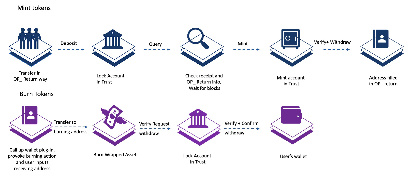
新公链时代的跨链安全性解决方案
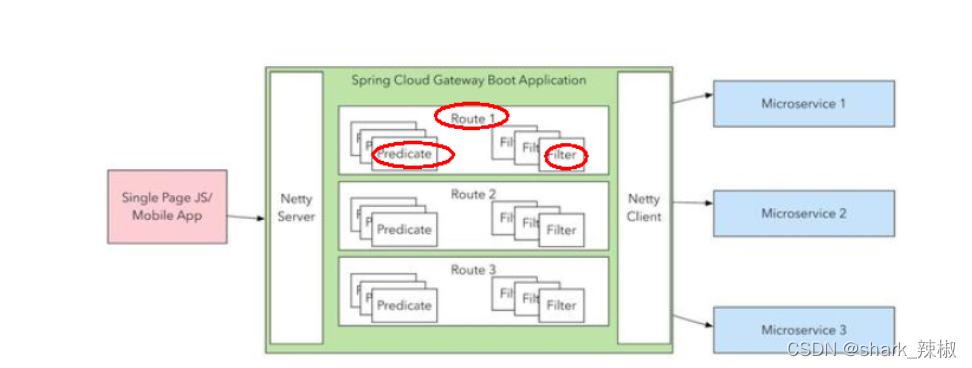
微服务-gateway【服务网关入门】
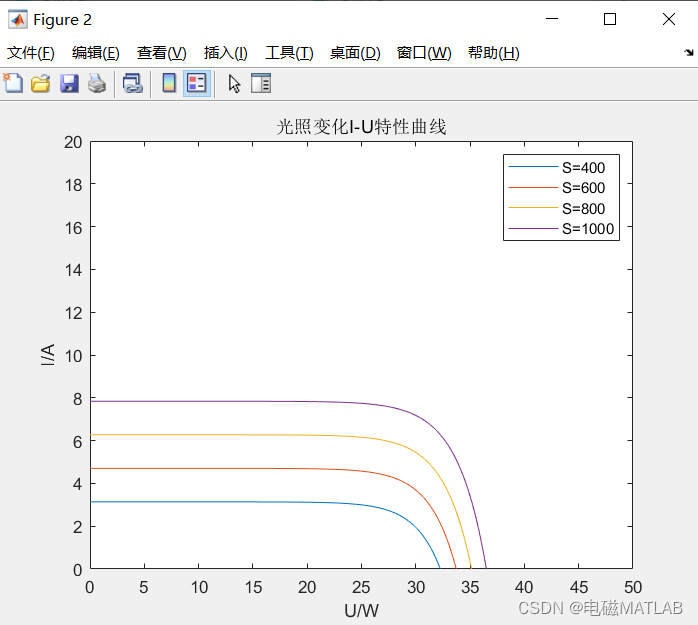
Mppt photovoltaic maximum power point tracking control matlab simulation

就刚刚,鸿蒙3.0发布了,华为还一口气发布了十一款产品
随机推荐
新公链时代的跨链安全性解决方案
中断向量表概述
详解卡尔曼滤波原理
如何正确地配置入口文件?
洛谷P5094 MooFest G 加强版
SQL Alias 别名
Mobile Banking Experience Test: How to Get the Real User Experience
【C语言刷题】双指针原地修改数组(力扣原题分析)
线程池原理与实践|从入门到放弃,深度解析
Mppt photovoltaic maximum power point tracking control matlab simulation
Sentinel vs Hystrix 限流对比,到底怎么选?
cache2go-源码阅读
3年半测试经验,20K我都没有,看来是时候跳槽了
有哪些好用的实时网络流量监控软件
通信大学生走向岗位,哪些技能最实用?
「日志」深度学习 CUDA环境配置
MySQL LIKE – 语法和用法示例教程
WPF使用Prism登录
药品研发--工艺技术人员积分和职务考核评估管理办法
How to mitigate the attack of corporate account hijacking?