当前位置:网站首页>pta a.1030的dijkstra+DFS方法
pta a.1030的dijkstra+DFS方法
2022-08-03 05:11:00 【二十八画之一】
这仅仅是我个人的做题笔记,内容来自《算法笔记》
前排的想法
关于dijkstra的一个小小变种,就是大多数时候距离最短不止一个,这样我们除了距离这个第一标准之外还会存在第二标准,这个第二标准怎么去找就成了一个问题,在a1030我们给了一种方法这里我们再给出一种办法——记录所有前置的结点,还原路线记录标准选怎最好的。
题目
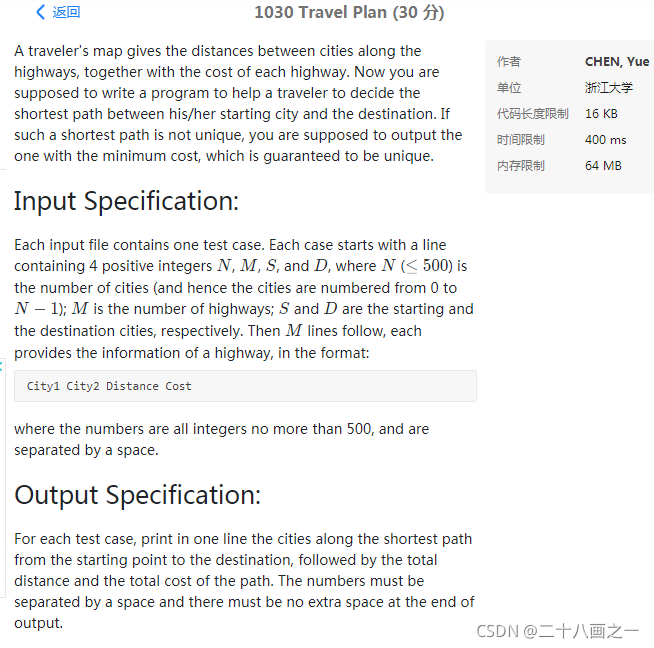
题目依旧是初中英文,我也没有什么理解错误。
思路
像前文说的那样一看到是最短路径,就用dijkstra(目前只会这个),然后去记录最短路径在遍历去比较第二标准(钱)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=510;
const int INF=0x3fffffff;
struct node{
int dis;
int cost;
};
node GM[MAXN][MAXN];
int dis[MAXN];
bool visit[MAXN];
vector<int> path,temp,pre[MAXN];
int n,m,s,d;
int mincost=INF;
void myfunc(int s);
void DFS(int s);
int main(void)
{
int a,b,c,e;
//int a,b,c,d; 第一处错误
scanf("%d%d%d%d",&n,&m,&s,&d);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
GM[i][j].cost=0;
GM[i][j].dis=INF;
}
}
for(int i=0;i<m;i++)
{
scanf("%d%d%d%d",&a,&b,&c,&e);
GM[a][b].dis=GM[b][a].dis=c;
GM[a][b].cost=GM[b][a].cost=e;
}
for(int i=0;i<n;i++)
{
dis[i]=INF;
visit[i]=false;
}
myfunc(s);
DFS(d);
for(int i=path.size()-1;i>=0;i--)
{
printf("%d ",path[i]);
}
printf("%d %d",dis[d],mincost);
return 0;
}
void myfunc(int v)
{
dis[v]=0;
int x,MIN;
for(int k=0;k<n;k++)
{
x=-1;
MIN=INF;
//第二处错误
for(int i=0;i<n;i++)
{
if(visit[i]==false&&dis[i]<MIN)
{
x=i;
MIN=dis[i];
}
}
if(x==-1)return ;
visit[x]=true;
for(int i=0;i<n;i++)
{
if(visit[i]==false&&GM[x][i].dis !=INF&&dis[i]>dis[x]+GM[x][i].dis )
{
dis[i]=dis[x]+GM[x][i].dis ;
pre[i].clear();
pre[i].push_back(x);
}
else if(visit[i]==false&&GM[x][i].dis !=INF&&dis[i]==dis[x]+GM[x][i].dis )
{
pre[i].push_back(x);
}
}
}
}
void DFS(int v)
{
if(v==s)
{
temp.push_back(v);
int value=0;
for(int i=0;i<temp.size()-1;i++)
{
value+=GM[temp[i]][temp[i+1]].cost ;
}
if(mincost>value)
{
mincost=value;
path=temp;//这里在写日志的时候要强调一下,path=temp之后你把temp清空也不会影响到path
}
temp.pop_back();
}
else
{
temp.push_back(v);
for(int i=0;i<pre[v].size();i++)
{
DFS(pre[v][i]);
//DFS(pre[v][i]); 第三处错误
}
temp.pop_back();
}
}
初学者错误 1
第一处 :我在外面有一个d是指目的地,但是我在随便设变量的时候有写了一个d导致错误
第二处 :我的}写错了位置
第三处 :遍历的时候忘了是遍历的什么了,直接把注释的写上了
分步来看
最短路径以及标记前缀
struct node{
int dis;
int cost;
};
node GM[MAXN][MAXN];
int dis[MAXN];
bool visit[MAXN];
vector<int> path,temp,pre[MAXN];
void myfunc(int v)
{
dis[v]=0;
int x,MIN;
for(int k=0;k<n;k++)
{
x=-1;
MIN=INF;
for(int i=0;i<n;i++)
{
if(visit[i]==false&&dis[i]<MIN)
{
x=i;
MIN=dis[i];
}
}
if(x==-1)return ;
visit[x]=true;
for(int i=0;i<n;i++)
{
if(visit[i]==false&&GM[x][i].dis !=INF&&dis[i]>dis[x]+GM[x][i].dis )
{
dis[i]=dis[x]+GM[x][i].dis ;
//1
pre[i].clear();
pre[i].push_back(x);
}
//2
else if(visit[i]==false&&GM[x][i].dis !=INF&&dis[i]==dis[x]+GM[x][i].dis )
{
pre[i].push_back(x);
}
}
}
}
其实就一点要说就是怎么储存前缀
这里注意一下因为可能不只有一条最短路径(如果是这样就不用那么麻烦了),所以对于前缀的储存用了一个可变数组vector。其实真正的改动只有一点点。
先说一个前提,我们知道dijkstra是用中介去调整,所以如果一个点可以调整那就意味着目前要到达这个点的最短路径要通过中介。
先说1这里,这里最需要注意的一点,是遇到一个新的最短路径时你要清空整个可变数组,因为你之前存了多少其实不重要,因为都不是最短,这点格外注意。清空之后加上新的。
再说2这里,说实话就是看到一样长的然后加上。
DFS找最短完善路径、
void DFS(int v)
{
if(v==s)
{
temp.push_back(v);
int value=0;
for(int i=0;i<temp.size()-1;i++)
{
value+=GM[temp[i]][temp[i+1]].cost ;
}
if(mincost>value)
{
mincost=value;
path=temp;//这里在写日志的时候要强调一下,path=temp之后你把temp清空也不会影响到path
}
temp.pop_back();
}
else
{
temp.push_back(v);
for(int i=0;i<pre[v].size();i++)
{
DFS(pre[v][i]);//1
}
temp.pop_back();//2
}
}
一个典型的DFS框架,仍有好多点需要注意
- 一定要清晰的知道自己在递归什么,我开始写的是DFS(i)但是显然不对,可是我第一次就是这样写的。思路一定要清晰。
- 关于退数组,说时候这是我第一次见,但是合情合理。这里说的是一个个的进无所谓但是当用完了的时候一定要记得退,多用情景模拟吧,目前我没有什么好办法。
- 比较在递归边界上,然后注意我写注释的那一点这个比较重要,这不仅仅是一个指针知道了好像是重新开辟了一个空间。
最后写一下能够构建起一个dijkstra的逻辑
1.寻找一个离起点最近的点纳入(通过以下的代码让起点被第一个纳入而不做特殊处理,这样才能够在处理的时候具有普遍性,例子见a1003)
for(int i=0;i<n;i++)
{
dis[i]=INF;
}
dis[v]=0;// v是指起点
2.用这个点作为中介点(x)去调整没有被纳入(visit[i]=false)、可以通过中介访问(GM[x][i]!=INF)的点的距离
3重复n次
其实仅仅是我犯的低级错误,但是对于题目是致命的 ︎
边栏推荐
猜你喜欢
随机推荐
处理异步事件的三种方式
斐讯K2路由编译Padavan华硕固件和心得
Odps temporary query can write SQL, turned out to a named?
Djiango第四次培训笔记
【扫雷】多方法超详细 7.28
dataframe插入一列
7.16(6)
vim命令
一劳永逸解决vs编译器无法使用scanf函数
第三次HarmonyOS培训
用C语言来实现五子棋小游戏
初步认识ZK
7.8(6)
MySQL 唯一索引 UNIQUE KEY 会导致死锁?
【三子棋】7.25
用scikit-learn学习谱聚类
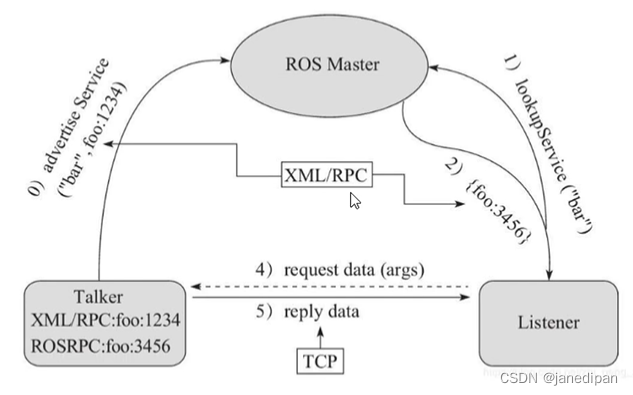
1.ROS环境搭建与基础工作
Go (二) 函数部分1 -- 函数定义,传参,返回值,作用域,函数类型,defer语句,匿名函数和闭包,panic
uni-app 滚动到顶部/指定位置
2. 两数相加