当前位置:网站首页>[set theory] set concept and relationship (true subset | empty set | complete set | power set | number of set elements | power set steps)
[set theory] set concept and relationship (true subset | empty set | complete set | power set | number of set elements | power set steps)
2022-07-03 04:06:00 【Programmer community】
List of articles
- One 、 True subset
- Two 、 An empty set
- 3、 ... and 、 The complete
- Four 、 Power set
- 5、 ... and 、 Number of collection elements
- 6、 ... and 、 Power set steps
One 、 True subset
True subset :
describe :
A
,
B
A , B
A,B Two sets , If
A
A
A aggregate yes
B
B
B A subset of a set , also
A
≠
B
A \not= B
A=B , said
A
A
A yes
B
B
B The proper subset of ,
B
B
B It really includes
A
A
A ;
Write it down as :
A
⊂
B
A \subset B
A⊂B
Symbolize :
A
⊂
B
A \subset B
A⊂B
⇔
\Leftrightarrow
⇔
A
⊆
B
∧
A
≠
B
A \subseteq B \land A \not= B
A⊆B∧A=B
Non proper subset :
describe :
A
A
A aggregate No
B
B
B The proper subset of a set ;
Write it down as :
A
⊄
B
A \not\subset B
A⊂B
Symbolize :
A
⊄
B
A \not\subset B
A⊂B
⇔
\Leftrightarrow
⇔
∃
x
(
x
∈
A
∧
x
∉
B
)
∧
A
≠
B
\exist x ( x \in A \land x \not\in B ) \land A \not= B
∃x(x∈A∧x∈B)∧A=B
( The element of being
x
x
x Is a collection
A
A
A The elements of , It's not a collection
B
B
B The elements of , also
A
,
B
A , B
A,B It's not equal , be
A
A
A No
B
B
B The proper subset of )
What a relationship nature :
Reflexivity :
A
⊄
A
A \not\subset A
A⊂A
Antisymmetry : If
A
⊂
B
A \subset B
A⊂B , that
B
⊄
A
B \not\subset A
B⊂A
Transitivity : If
A
⊂
B
A \subset B
A⊂B , also
B
⊂
C
B \subset C
B⊂C , that
A
⊂
C
A \subset C
A⊂C
Two 、 An empty set
Empty set description : A collection without any elements , It is called an empty set , Referred to as An empty set ;
Write it down as :
∅
\varnothing
∅
Empty set example :
A
=
{
x
∣
x
2
+
1
=
0
∧
x
∈
R
}
A = \{ x | x^2 + 1 = 0 \land x \in R \}
A={ x∣x2+1=0∧x∈R}
R
R
R Is a set of real numbers , Above
x
x
x Obviously, there is no solution , Set is also empty ;
Empty set theorem : An empty set is a subset of all sets ;
Empty set inference : Empty sets are unique ;
3、 ... and 、 The complete
The complete : Limit the set in question , Are subsets of a set , The set is called a complete set , Write it down as
E
E
E ;
It's not unique : The complete set is only relative to the scope of discussing problems , Is not the only , You cannot discuss situations outside the scope ;
Examples of complete works : Discuss [0, 1] Properties of real numbers on intervals , Take the complete set as [0, 1] All real numbers on ;
( Discuss the numbers of other intervals , You can also take other intervals as the complete set )
Four 、 Power set
Power set description :
A
A
A It's a collection ,
A
A
A A set consisting of all subsets of a set be called
A
A
A Power set of ;
Write it down as :
P
(
A
)
P(A)
P(A)
Symbolic expression :
P
(
A
)
=
{
x
∣
x
⊆
A
}
P(A) = \{ x | x \subseteq A \}
P(A)={ x∣x⊆A}
5、 ... and 、 Number of collection elements
Number of collection elements :
0
0
0 Meta set :
∅
\varnothing
∅
1
1
1 Meta set : contain
1
1
1 Collection of elements , Also known as Unit set ;
2
2
2 Meta set : contain
2
2
2 Collection of elements ;
⋮
\vdots
⋮
n
n
n Meta set : contain
n
n
n Collection of elements ; (
n
≥
1
n \geq 1
n≥1 )
There are poor sets :
∣
A
∣
|A|
∣A∣ Represents a collection
A
A
A The number of elements in , If
A
A
A The number of elements in the set is Finite number when , Then call it
A
A
A A set is a finite set , or Limited set ;
Theorem of the number of power sets : aggregate
A
A
A Medium Element number
∣
A
∣
=
n
|A| = n
∣A∣=n , be
A
A
A Of Number of power sets
∣
P
(
A
)
∣
=
2
n
|P(A)| = 2^n
∣P(A)∣=2n ;
6、 ... and 、 Power set steps
Power set steps : seek aggregate
A
A
A Power set of , It needs to be calculated in order
A
A
A Collection All subsets from low to high elements , Then these subsets are combined into a set ;
All subsets of low to high elements :
0
0
0 Meta set ,
1
1
1 Meta set ,
2
2
2 Meta set ,
⋯
\cdots
⋯ ,
n
n
n Meta set ;
aggregate
A
=
{
a
,
b
,
c
}
A = \{ a, b , c \}
A={ a,b,c}
0
0
0 Meta set :
∅
\varnothing
∅
1
1
1 Meta set :
{
a
}
\{ a \}
{ a} ,
{
b
}
\{ b \}
{ b} ,
{
c
}
\{ c \}
{ c}
2
2
2 Meta set :
{
a
,
b
}
\{ a, b \}
{ a,b} ,
{
a
,
c
}
\{ a, c \}
{ a,c} ,
{
b
,
c
}
\{ b, c \}
{ b,c}
3
3
3 Meta set :
{
a
,
b
,
c
}
\{ a, b, c \}
{ a,b,c}
aggregate
A
A
A The power set of is :
P
(
A
)
=
{
∅
,
{
a
}
,
{
b
}
,
{
c
}
,
{
a
,
b
}
,
{
a
,
c
}
,
{
b
,
c
}
,
{
a
,
b
,
c
}
}
P(A) = \{ \varnothing , \{ a \} , \{ b \} , \{ c \} , \{ a, b \} , \{ a, c \} , \{ b, c \} , \{ a, b, c \} \}
P(A)={ ∅,{ a},{ b},{ c},{ a,b},{ a,c},{ b,c},{ a,b,c}}
边栏推荐
- Practical operation of vim
- DAPP for getting started with eth
- MySQL create table
- Web session management security issues
- Design and implementation of kubelet garbage collection mechanism to protect nodes from being preempted by containers image GC high threshold
- QSAR model establishment script based on pytoch and rdkit
- JS realizes lazy loading of pictures
- Is pytorch open source?
- 8.8.2-PointersOnC-20220214
- js实现在可视区内,文字图片动画效果
猜你喜欢
用户体验五要素

2022 mobile crane driver examination registration and mobile crane driver operation examination question bank

2022deepbrainchain biweekly report no. 104 (01.16-02.15)

CVPR 2022 | 大連理工提出自校准照明框架,用於現實場景的微光圖像增强

IPv6 transition technology-6to4 manual tunnel configuration experiment -- Kuige of Shangwen network

国产PC系统完成闭环,替代美国软硬件体系的时刻已经到来
![[Apple Push] IMessage group sending condition document (push certificate) development tool pushnotification](/img/30/c840e28c0ef7c8ce574dcde4363863.jpg)
[Apple Push] IMessage group sending condition document (push certificate) development tool pushnotification

300+ documents! This article explains the latest progress of multimodal learning based on transformer
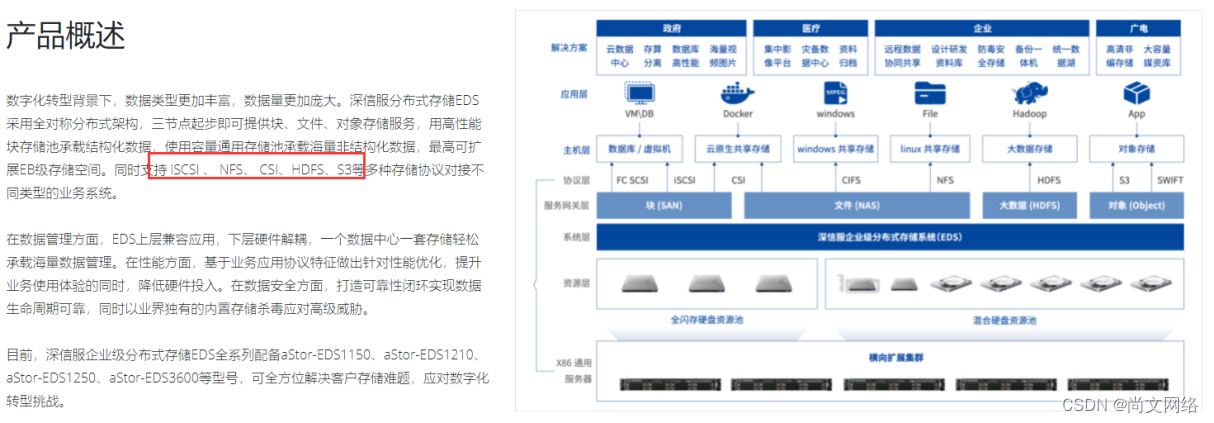
CEPH Shangwen network xUP Nange that releases the power of data

Download and install captura and configure ffmpeg in captura
随机推荐
2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
Appium automated testing framework
The 10th China Cloud Computing Conference · China Station: looking forward to the trend of science and technology in the next decade
300+ documents! This article explains the latest progress of multimodal learning based on transformer
Recursion: one dimensional linked lists and arrays
Debug: CD cannot be used in kaggle
Makefile demo
The latest analysis of the main principals of hazardous chemical business units in 2022 and the simulated examination questions of the main principals of hazardous chemical business units
CVPR 2022 | 大连理工提出自校准照明框架,用于现实场景的微光图像增强
Wechat applet + Alibaba IOT platform + Hezhou air724ug built with server version system analysis
[brush questions] find the number pair distance with the smallest K
How to download pytorch? Where can I download pytorch?
Bisher - based on SSM pet adoption center
"Final review" 16/32-bit microprocessor (8086) basic register
错误 C2694 “void Logger::log(nvinfer1::ILogger::Severity,const char *)”: 重写虚函数的限制性异常规范比基类虚成员函数
C language hashtable/hashset library summary
[learning notes] seckill - seckill project - (11) project summary
2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
MySQL create table
"Designer universe" argument: Data Optimization in the design field is finally reflected in cost, safety and health | chinabrand.com org