当前位置:网站首页>[mathematical logic] predicate logic (toe normal form | toe normal form conversion method | basic equivalence of predicate logic | name changing rules | predicate logic reasoning law)
[mathematical logic] predicate logic (toe normal form | toe normal form conversion method | basic equivalence of predicate logic | name changing rules | predicate logic reasoning law)
2022-07-03 04:02:00 【Programmer community】
List of articles
- One 、 The toe in paradigm
- Two 、 The method of toe in normal form transformation
- 3、 ... and 、 Example of toe in paradigm
- Four 、 Predicate logic inference law
One 、 The toe in paradigm
The formula
A
A
A There are the following forms :
Q
1
x
1
Q
2
x
2
⋯
Q
k
x
k
B
Q_1 x_1 Q_2 x_2 \cdots Q_kx_k B
Q1x1Q2x2⋯QkxkB
said
A
A
A yes The toe in paradigm ; The toe in paradigm
A
A
A Related elements of explain :
quantifiers :
Q
i
Q_i
Qi It's a quantifier , Full name quantifier
∀
\forall
∀ , or There are quantifiers
∃
\exist
∃ ;
Guide arguments :
x
i
x_i
xi yes Guide arguments ;
B
B
B The formula :
B
B
B Is a predicate logic formula , There are no quantifiers ,
B
B
B in Can contain Ahead
x
1
,
x
2
,
⋯
,
x
k
x_1 , x_2 , \cdots , x_k
x1,x2,⋯,xk Guide arguments , also May not contain Some of these arguments ;
(
B
B
B Must not contain quantifiers )
Two 、 The method of toe in normal form transformation
Find a prefix normal form of predicate logic formula , Use Basic equivalence , or Name change rules ;
Basic equivalence : Reference blog 【 Mathematical logic 】 Predicate logic ( Basic equivalence of predicate logic | Eliminate quantifier equivalents | The quantifier negates the equivalent | The scope of quantifier is shrinking and expanding | The equivalent of quantifier distribution )
Name change rules : The formula
A
A
A in , In a quantifier domain , A constraint The emergence of Individual variables Corresponding Guide arguments
x
i
x_i
xi , Use the formula
A
A
A That didn't show up in Argument
x
j
x_j
xj Replace , The resulting formula
A
′
⇔
A
A' \Leftrightarrow A
A′⇔A ;
Such as :
∀
x
F
(
x
)
∨
∀
x
¬
G
(
x
,
y
)
\forall x F(x) \lor \forall x \lnot G(x, y)
∀xF(x)∨∀x¬G(x,y) If its toe in paradigm is required , There are two before and after
x
x
x , Here we use the name change rule , Replace one with something that has never appeared Guide arguments
z
z
z , Change the name to
∀
x
F
(
x
)
∨
∀
z
¬
G
(
z
,
y
)
\forall x F(x) \lor \forall z \lnot G(z, y)
∀xF(x)∨∀z¬G(z,y) ;
3、 ... and 、 Example of toe in paradigm
seek
∀
x
F
(
x
)
∨
¬
∃
x
G
(
x
,
y
)
\forall x F(x) \lor \lnot \exist x G(x, y)
∀xF(x)∨¬∃xG(x,y) The toe in paradigm ;
The above formula is not a toe in paradigm , Its quantifiers
∀
x
\forall x
∀x Our jurisdiction is
F
(
x
)
F(x)
F(x) , quantifiers
∃
x
\exist x
∃x Our jurisdiction is
G
(
x
,
y
)
G(x, y)
G(x,y) , Neither jurisdiction covers the complete formula ;
Use Equivalent calculus and Name change rules , Find the foreskin normal form ;
∀
x
F
(
x
)
∨
¬
∃
x
G
(
x
,
y
)
\forall x F(x) \lor \lnot \exist x G(x, y)
∀xF(x)∨¬∃xG(x,y)
Use The quantifier negates the equivalent , The first Negative connectives Move to the back of the quantifier , The equivalent formula used is
¬
∃
x
A
(
x
)
⇔
∀
x
¬
A
(
x
)
\lnot \exist x A(x) \Leftrightarrow \forall x \lnot A(x)
¬∃xA(x)⇔∀x¬A(x) ;
⇔
∀
x
F
(
x
)
∨
∀
x
¬
G
(
x
,
y
)
\Leftrightarrow \forall x F(x) \lor \forall x \lnot G(x, y)
⇔∀xF(x)∨∀x¬G(x,y)
Use Name change rules , Put the second
∀
x
¬
G
(
x
,
y
)
\forall x \lnot G(x, y)
∀x¬G(x,y) Medium
x
x
x Switch to
z
z
z ;
⇔
∀
x
F
(
x
)
∨
∀
z
¬
G
(
z
,
y
)
\Leftrightarrow \forall x F(x) \lor \forall z \lnot G(z, y)
⇔∀xF(x)∨∀z¬G(z,y)
Use Equivalent formula of scope expansion , take
∀
x
\forall x
∀x Scope expansion , The equivalent formula used is
∀
x
(
A
(
x
)
∨
B
)
⇔
∀
x
A
(
x
)
∨
B
\forall x ( A(x) \lor B ) \Leftrightarrow \forall x A(x) \lor B
∀x(A(x)∨B)⇔∀xA(x)∨B
⇔
∀
x
(
F
(
x
)
∨
∀
z
¬
G
(
z
,
y
)
)
\Leftrightarrow \forall x ( F(x) \lor \forall z \lnot G(z, y) )
⇔∀x(F(x)∨∀z¬G(z,y))
Again using Equivalent formula of scope expansion , take
∀
z
\forall z
∀z Scope expansion , The equivalent formula used is
∀
x
(
A
(
x
)
∨
B
)
⇔
∀
x
A
(
x
)
∨
B
\forall x ( A(x) \lor B ) \Leftrightarrow \forall x A(x) \lor B
∀x(A(x)∨B)⇔∀xA(x)∨B
⇔
∀
x
∀
z
(
F
(
x
)
∨
¬
G
(
z
,
y
)
)
\Leftrightarrow \forall x \forall z ( F(x) \lor \lnot G(z, y) )
⇔∀x∀z(F(x)∨¬G(z,y))
At this time, it is the toe in paradigm ;
Use Propositional logic Equivalent formula Medium Implication equivalence
⇔
∀
x
∀
z
(
G
(
z
,
y
)
→
F
(
x
)
)
\Leftrightarrow \forall x \forall z ( G(z, y) \to F(x) )
⇔∀x∀z(G(z,y)→F(x))
Four 、 Predicate logic inference law
The following reasoning law is one-way , From the left, we can infer the right , You can't infer from the right to the left ; ( Not equivalent )
①
∀
x
A
(
x
)
∨
∀
x
B
(
x
)
⇒
∀
x
(
A
(
x
)
∨
B
(
x
)
)
\rm \forall x A(x) \lor \forall x B(x) \Rightarrow \forall x ( A(x) \lor B(x) )
∀xA(x)∨∀xB(x)⇒∀x(A(x)∨B(x))
Corresponding Full name quantifier Distribution rate , In the equation Only applicable to Conjunctions , Because of the above Disjunction time , From right to left It's wrong. , You can only reason from left to right ;
②
∃
x
(
A
(
x
)
∧
B
(
x
)
)
⇒
∃
x
A
(
x
)
∧
∃
x
B
(
x
)
\rm \exist x ( A(x) \land B(x) ) \Rightarrow \exist x A(x) \land \exist x B(x)
∃x(A(x)∧B(x))⇒∃xA(x)∧∃xB(x)
③
∀
x
(
A
(
x
)
→
B
(
x
)
)
⇒
∀
x
A
(
x
)
→
∀
x
B
(
x
)
\rm \forall x ( A(x) \to B(x) ) \Rightarrow \forall x A(x) \to \forall x B(x)
∀x(A(x)→B(x))⇒∀xA(x)→∀xB(x)
④
∀
x
(
A
(
x
)
→
B
(
x
)
)
⇒
∃
x
A
(
x
)
→
∃
x
B
(
x
)
\rm \forall x ( A(x) \to B(x) ) \Rightarrow \exist x A(x) \to \exist x B(x)
∀x(A(x)→B(x))⇒∃xA(x)→∃xB(x)
边栏推荐
- 2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
- 阿洛对自己的思考
- [brush questions] connected with rainwater (one dimension)
- Deep dive kotlin synergy (19): flow overview
- CVPR 2022 | 大连理工提出自校准照明框架,用于现实场景的微光图像增强
- 有监督预训练!文本生成又一探索!
- What is pytorch? Is pytorch a software?
- 服务器无法远程连接原因分析
- Mila、渥太华大学 | 用SE(3)不变去噪距离匹配进行分子几何预训练
- ZIP文件的导出
猜你喜欢
2022 P cylinder filling examination content and P cylinder filling practice examination video

pytorch项目怎么跑?
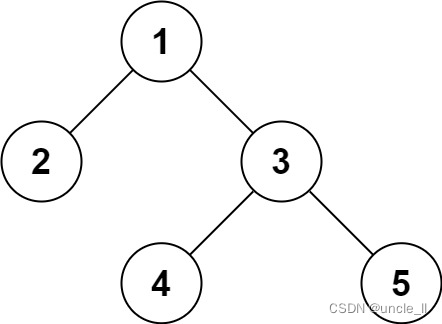
leetcode:297. 二叉树的序列化与反序列化

CVPR 2022 | Dalian Institute of technology proposes a self calibration lighting framework for low light level image enhancement of real scenes

Deep dive kotlin synergy (19): flow overview

【毕业季·进击的技术er】职场人的自白
js中#号的作用

2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video

Appium自动化测试框架
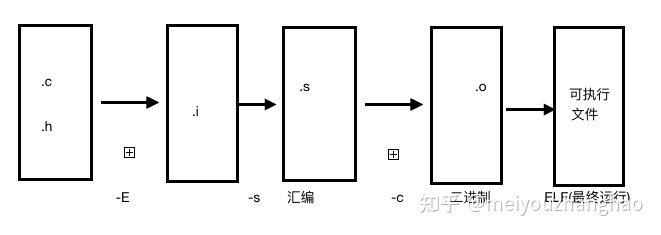
Makefile demo
随机推荐
Appium自动化测试框架
【刷题篇】接雨水(一维)
Commands related to the startup of redis under Linux server (installation and configuration)
用户体验五要素
Bisher - based on SSM pet adoption center
2022-07-02:以下go语言代码输出什么?A:编译错误;B:Panic;C:NaN。 package main import “fmt“ func main() { var a =
Null and undefined
Is it better to speculate in the short term or the medium and long term? Comparative analysis of differences
动态规划:最长回文子串和子序列
CVPR 2022 | 大連理工提出自校准照明框架,用於現實場景的微光圖像增强
[Blue Bridge Road -- bug free code] interpretation of some codes of matrix keyboard
Separable bonds and convertible bonds
"Designer universe" argument: Data Optimization in the design field is finally reflected in cost, safety and health | chinabrand.com org
Web会话管理安全问题
树莓派如何连接WiFi
没有sXid,suid&sgid将进入险境!-尚文网络xUP楠哥
第十届中国云计算大会·中国站:展望未来十年科技走向
[learning notes] seckill - seckill project - (11) project summary
2.14 simulation summary
2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video