[search] two way search + A*

---

Two way search

Generally used to solve “ The minimum number of steps ” Model problem

Two way wide search can avoid wasting time on deep subtrees .

In some questions , Not only the problem have “ Initial state ”, also Have a clear “ Terminal state ”, And the search tree generated by reverse search from the initial state to the final state can cover the entire state space .

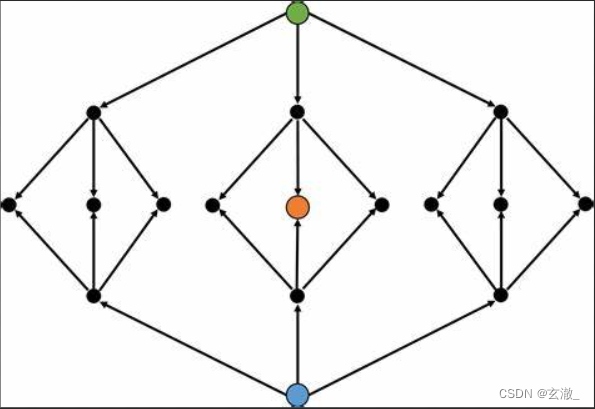
Under such conditions , May adopt Two way search —— Starting from the initial state and the final state, search for half the states respectively , Generate two search trees with half the depth , Meet in the middle , Combine into the final answer .

---

AcWing 190. String transformation  （ Two way search ）

 

sample input ：

abcd xyz
abc xu
ud y
y yz

sample output ：

3

---

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

const int N = 6;

int n;
string A, B;
string a[N], b[N];

int extend(queue<string>& q, unordered_map<string, int>&da, unordered_map<string, int>& db, 
    string a[N], string b[N])
{
    int d = da[q.front()];
    while (q.size() && da[q.front()] == d)
    {
        auto t = q.front();
        q.pop();

        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < t.size(); j ++ )
                if (t.substr(j, a[i].size()) == a[i])
                {
                    string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size());
                    if (db.count(r)) return da[t] + db[r] + 1;
                    if (da.count(r)) continue;
                    da[r] = da[t] + 1;
                    q.push(r);
                }
    }

    return 11;
}

int bfs()
{
    if (A == B) return 0;
    queue<string> qa, qb;
    unordered_map<string, int> da, db;

    qa.push(A), qb.push(B);
    da[A] = db[B] = 0;

    int step = 0;
    while (qa.size() && qb.size())
    {
        int t;
        if (qa.size() < qb.size()) t = extend(qa, da, db, a, b);
        else t = extend(qb, db, da, b, a);

        if (t <= 10) return t;
        if ( ++ step == 10) return -1;
    }

    return -1;
}

int main()
{
    cin >> A >> B;
    while (cin >> a[n] >> b[n]) n ++ ;

    int t = bfs();
    if (t == -1) puts("NO ANSWER!");
    else cout << t << endl;

    return 0;
}

---

A* 

About priority queues BFS Algorithm , The algorithm maintains a priority queue （ Binary heap ）, Keep getting out of the heap “ The current cost is the least ” The state of （ Top of pile ） Expand . When each state is first removed from the heap , We get the minimum cost from the initial state to this state .

If given a “ Target state ”, We need to find the minimum cost from the initial state to the target state , Your priority queue BFS This “ Priority strategy ” Is not perfect . The current cost of a state is minimal , It only shows that the cost from the starting point to this state is very small , And in the future search , It may cost a lot to go from this state to the target state . in addition , Some states, although the current cost is slightly higher , But the cost of reaching the target state in the future may be small , So the total cost from the initial state to the target state is better .

Priority queue BFS Choose the branch of the former first , As a result, the amount of search for the optimal solution increases . In order to improve efficiency , It can be done to Estimate the possible costs in the future .

We can design a “ Valuation function ”, With “ Any state ” For input , Calculate the estimated cost of moving from this state to the target state . In search , A heap still needs to be maintained , Keep getting out of the heap “ The current cost + Future valuation ” Expand the minimum state .

In order to ensure that the optimal solution is obtained when the target state is taken out of the heap for the first time , The valuation function we designed needs to meet a basic criterion

Set the current state state The estimate required to reach the target state is f(state)

Set in future search , Actually find out from the current state state  The minimum cost of reaching the target state is g(state)

For arbitrary  state , Should have  

in other words , The valuation of the valuation function cannot be greater than the actual future cost , The valuation is better than the actual cost

---

AcWing 179. Eight digital

 

sample input ：

2  3  4  1  5  x  7  6  8 

sample output

ullddrurdllurdruldr

---

Valuation function ： The sum of Manhattan distances between each number in the current state and its target location

---

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

int f(string state)
{
    int res = 0;
    for (int i = 0; i < state.size(); i ++ )
        if (state[i] != 'x')
        {
            int t = state[i] - '1';
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
        }
    return res;
}

string bfs(string start)
{
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    char op[4] = {'u', 'r', 'd', 'l'};

    string end = "12345678x";
    unordered_map<string, int> dist;
    unordered_map<string, pair<string, char>> prev;
    priority_queue<pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> heap;

    heap.push({f(start), start});
    dist[start] = 0;

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        string state = t.second;

        if (state == end) break;

        int step = dist[state];
        int x, y;
        for (int i = 0; i < state.size(); i ++ )
            if (state[i] == 'x')
            {
                x = i / 3, y = i % 3;
                break;
            }
        string source = state;
        for (int i = 0; i < 4; i ++ )
        {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
                swap(state[x * 3 + y], state[a * 3 + b]);
                if (!dist.count(state) || dist[state] > step + 1)
                {
                    dist[state] = step + 1;
                    prev[state] = {source, op[i]};
                    heap.push({dist[state] + f(state), state});
                }
                swap(state[x * 3 + y], state[a * 3 + b]);
            }
        }
    }

    string res;
    while (end != start)
    {
        res += prev[end].second;
        end = prev[end].first;
    }
    reverse(res.begin(), res.end());
    return res;
}

int main()
{
    string g, c, seq;
    while (cin >> c)
    {
        g += c;
        if (c != "x") seq += c;
    }

    int t = 0;
    for (int i = 0; i < seq.size(); i ++ )
        for (int j = i + 1; j < seq.size(); j ++ )
            if (seq[i] > seq[j])
                t ++ ;

    if (t % 2) puts("unsolvable");
    else cout << bfs(g) << endl;

    return 0;
}

---

AcWing 178. The first K A short circuit  

 

 

sample input ：

2 2
1 2 5
2 1 4
1 2 2

sample output ：

14

---

use Dijkstra The idea of the shortest path , Every expansion The shortest path , The first k The length of the path when reaching the destination for the second time is k Length of short circuit .

Because the algorithm is equivalent to simultaneous k  The shortest circuit of secondary unit , Time and space may exceed the limit , therefore Preprocess the shortest distance from each point to the end point as the evaluation function , utilize A∗ Algorithm optimization .

The complexity is

---

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
typedef pair<int, PII> PIII;

const int N = 1010, M = 200010;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[], int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dijkstra()
{
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, T});

    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y;
        if (st[ver]) continue;
        st[ver] = true;

        for (int i = rh[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
}

int astar()
{
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    heap.push({dist[S], {0, S}});

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y.y, distance = t.y.x;
        cnt[ver] ++ ;
        if (cnt[T] == K) return distance;

        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (cnt[j] < K)
                heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
        }
    }

    return -1;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(h, a, b, c);
        add(rh, b, a, c);
    }
    scanf("%d%d%d", &S, &T, &K);
    if (S == T) K ++ ;

    dijkstra();
    printf("%d\n", astar());

    return 0;
}