当前位置:网站首页>Binary search tree (search binary tree) simulation implementation (there is a recursive version)
Binary search tree (search binary tree) simulation implementation (there is a recursive version)
2022-08-03 10:49:00 【Han Xuanzi】
二叉搜索数
1.二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树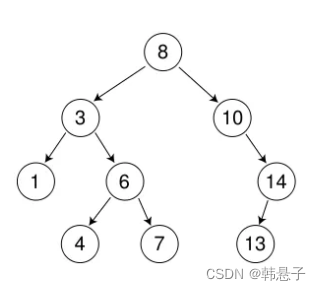
2.insert和find和InOrder实现
就讲一下insert怎么实现,分为二种情况,One is that the binary tree is empty,Another non-null insert,第一种很好解决,第二种,因为要满足,Searching for the left subtree of a binary tree is smaller than the heel,The right subtree is larger than the heel,Then we just need to use the inserted number and the root to compare the size,Access the right if the root is less than the number inserted,The left side is accessed if the root is greater than the number inserted,Keep looping until an empty node is found,Finally, find the place to insert it,But it is unclear whether the position to be inserted is left or right,Then it is very simple to record the parent node of this node and compare the size,Left smaller than the parent node,Larger to the right than the parent node.
findThis is also simple and practicalinsertThe same visit to an empty node means not found,The found case is the number to be found in the loop,Left and right trees that are not smaller or larger than the root
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{
}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool insert(const K& key)
{
//为空的时候
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right=cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root=nullptr;
};
void TestBSTree()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.insert(16);
t.insert(9);
t.InOrder();
}
运行结果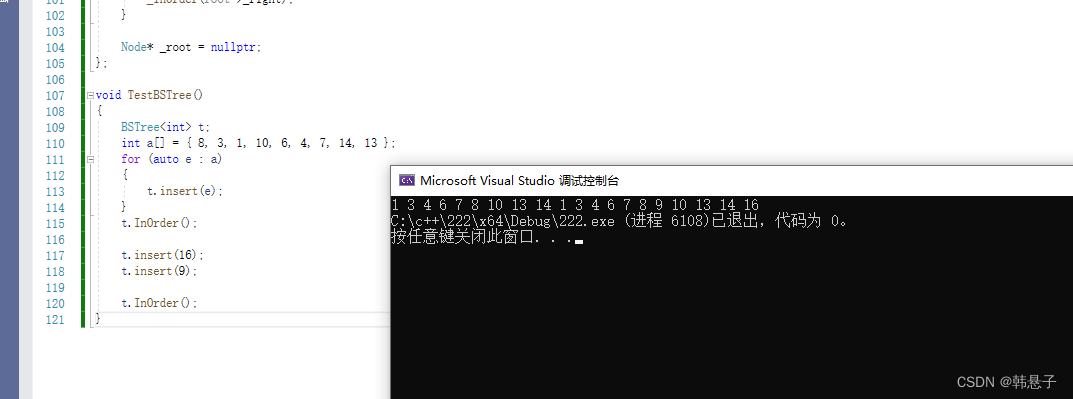
3.erase实现
If you want to delete it, you must traverse it first,Deleted into
a. 要删除的结点无孩子结点
b. The node to be deleted has only one child,左为空或右为空
d. 要删除的结点有左、右孩子结点
etc. to be realized
With only one child:The node to be considered for deletion isleft还是right为空,并且还要考虑,It may be the case that only the root left subtree has no right subtree,Or the case where the root right subtree has no left subtree,After all, the principle is to deletecur,Make the left or right of the parent node point to the left or right of the node to be deleted
有左右节点:Let the node to delete and the node to deleterightmedium minimum exchange,或者覆盖,Then delete the node to be deleted
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
//if(cur==nullptr)
if (cur == _root)//There is no left subtree problem
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//if(cur==nullptr)
if (cur == _root)//There is no right subtree problem
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//Both children are empty
{
// Minimum node substitution for the right subtree
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
swap(minRight->_key, cur->_key);
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void TestBSTree1()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.Erase(3);
t.Erase(8);
t.InOrder();
t.Erase(14);
t.Erase(7);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}
运行结果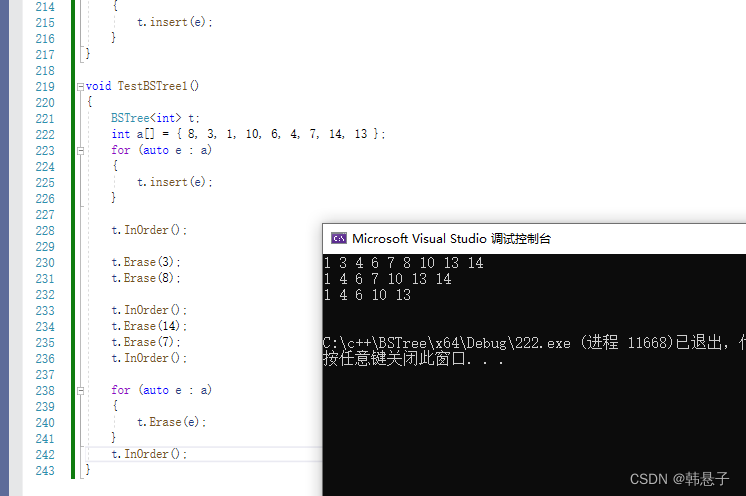
4.Construct assignment destructor implementation
// 强制编译器自己生成构造
// C++11
BSTree() = default;
BSTree(const BSTree<K>&t)
{
_root = CopyTree(t._root);
}
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
Node* CopyTree(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = CopyTree(root->_left);
copyNode->_right = CopyTree(root->_right);
return copyNode;
}
~BSTree()
{
DestoryTree(_root);
_root = nullptr;
}
void DestoryTree(Node* root)
{
if (root == nullptr)
return;
DestoryTree(root->_left);
DestoryTree(root->_right);
delete root;
}
5.迭代查找
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
6.递归插入
Quotedroot就是父亲节点
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
递归展开图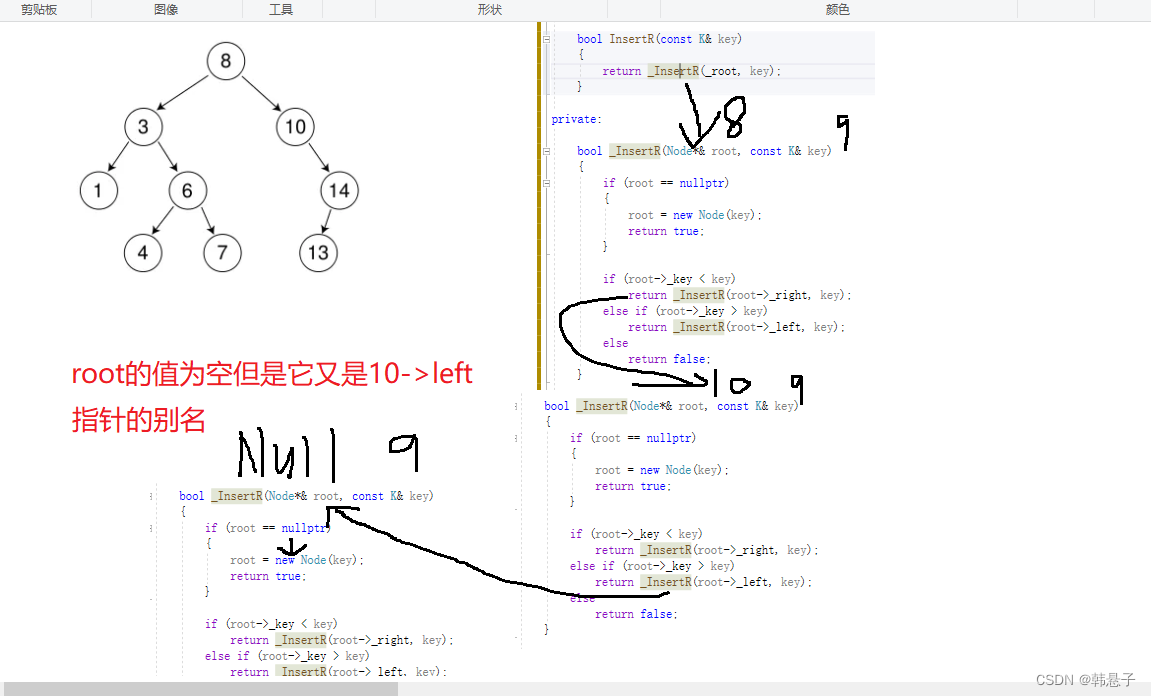
7.递归删除
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
8.Search all codes of binary tree plus recursive writing
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{
}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
// 强制编译器自己生成构造
// C++11
BSTree() = default;
BSTree(const BSTree<K>&t)
{
_root = CopyTree(t._root);
}
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
DestoryTree(_root);
_root = nullptr;
}
bool find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool insert(const K& key)
{
//为空的时候
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
//if(cur==nullptr)
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//if(cur==nullptr)
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//Both children are empty
{
// Minimum node substitution for the right subtree
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
swap(minRight->_key, cur->_key);
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
///
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
Node* CopyTree(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = CopyTree(root->_left);
copyNode->_right = CopyTree(root->_right);
return copyNode;
}
void DestoryTree(Node* root)
{
if (root == nullptr)
return;
DestoryTree(root->_left);
DestoryTree(root->_right);
delete root;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root = nullptr;
};
void TestBSTree()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.insert(16);
t.insert(9);
t.InOrder();
t.Erase(8);
for (auto e : a)
{
t.insert(e);
}
}
void TestBSTree1()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.Erase(3);
t.Erase(8);
t.InOrder();
t.Erase(14);
t.Erase(7);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}
void TestBSTree4()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
BSTree<int> copy = t;
copy.InOrder();
}
边栏推荐
- 训练双塔检索模型,可以不用query-doc样本了?明星机构联合发文
- CADEditorX ActiveX 14.1.X
- 优炫数据库在linux平台下服务启动失败的原因
- 玉溪卷烟厂通过正确选择时序数据库 轻松应对超万亿行数据
- Depth study of 100 cases - convolution neural network (CNN) to realize the clothing image classification
- Apache Doris系列之:数据模型
- 成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
- Machine Learning Overview
- json格式的字符串是什么类型的_输入字符串的格式要求
- HCIP第十七天笔记
猜你喜欢
随机推荐
安全研究员:大量Solana钱包被盗
简述设计的意义是什么_定义和概念的最大区别
This article understands the process from RS485 sensor to IoT gateway to cloud platform
MATLAB programming and application 2.7 Structural data and unit data
Interview Blitz 71: What's the difference between GET and POST?
for in 和 for of的区别
成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
被审稿人吐槽没有novelty!深度学习方向怎么找创新点?
MySQL数据库高级使用
gbase在轨道交通一般都采用哪种高可用架构?
记某社区问答
3D激光SLAM:LeGO-LOAM---两步优化的帧间里程计及代码分析
MySQL中tinytext、text、mediumtext和longtext等各个类型详解[通俗易懂]
4G采集ModbusTCP转JSON接MQTT云平台
巴比特 | 元宇宙每日必读:玩家离场,平台关停,数字藏品市场正逐渐降温,行业的未来究竟在哪里?...
With strong network, China mobile to calculate excitation surging energy network construction
浪潮—英伟达打造元宇宙新方案,虚拟人的故事将再破你的认知
Mysql OCP 75 questions
大佬们,我遇到一个问题:我源端mysql有一张一直在写入的表,我使用mysql cdc connec
像用户体验设计师一样思考