当前位置:网站首页>Linear model of machine learning
Linear model of machine learning
2022-06-12 11:55:00 【In the same breath SEG】
Catalog
What is a linear model
Linear model is to use a polynomial function to represent the relationship between input and output , Its form is as follows :
y = w 1 ∗ x 1 + w 2 ∗ x 2 + . . . w d ∗ x d + b (1) y = w_1*x_1+w_2*x_2+... w_d*x_d+b\tag{1} y=w1∗x1+w2∗x2+...wd∗xd+b(1)
among x i x_i xi Represent different attributes , y y y Represents the predicted value of the model . It can be written in the form of the following vector :
y = W T ∗ x + b (2) y=W^T*x+b\tag{2} y=WT∗x+b(2)
The linear model is the simplest model , Many nonlinear models are improved on the basis of it , Because we can use the coefficient matrix W W W To determine which attribute is more important to the prediction results , Therefore, its explicability is relatively strong . Here are some classical linear models .
Linear regression
Linear regression attempts to learn a linear model to predict real value output markers as accurately as possible , That is, the purpose of linear regression model is to find (2) Coefficient matrix in W W W And the constant term b b b bring y ( x i ) ≈ y i (3) y(x_i) \approx y_i\tag{3} y(xi)≈yi(3) among , y ( x i ) y(x_i) y(xi) Is the predicted value of the model , y i y_i yi Is the true value of the example . The smaller the deviation between the predicted value and the true value, the better , Mean square error can be used as a performance measure , That is, by minimizing the mean square error W W W and b b b , Mean square error has a good geometric meaning , Because it corresponds to the commonly used Euclidean distance . The method of solving the model based on the minimization of mean square error is called least square method , Introduction of least square method there are many on the Internet , I won't go into details here .
Sometimes , We can also let the model approach the real valued output marked function , For example, the model is expressed in the following form :
ln y = W T ∗ x + b (4) \ln y=W^T*x+b\tag{4} lny=WT∗x+b(4)
This is logarithmic linear regression , Is actually trying to make e W T ∗ x + b e^{W^T*x+b} eWT∗x+b To approach y y y, In essence, it is to find the nonlinear function mapping from input space to output space , So we call similar linear regression generalized linear model , Its form is as follows :
y = g − 1 ( W T ∗ x + b ) (5) y=g^{-1}(W^T*x+b)\tag{5} y=g−1(WT∗x+b)(5)
among g ( ⋅ ) g( \cdot ) g(⋅) It's called the connection function (link function), Continuous and sufficiently smooth , The parameter estimation of generalized linear model often needs to be carried out by weighted least square method or maximum likelihood method .
Log probability regression
Logarithmic probability regression although the name is regression , But it's actually a classified learning method , To apply linear regression models to classification problems , You need to find a monotone , The differentiable function marks the actual classification task y y y Linked to the predicted value of the linear regression model output , Logarithmic probability function is an ideal function , Substitute the logarithmic probability function into (5) have to :
y = 1 1 + e − ( W T ∗ x + b ) (6) y= \frac{1}{1+{e^{-(W^T*x+b)}}}\tag{6} y=1+e−(WT∗x+b)1(6) Can be changed into :
ln y 1 − y = W T x + b (7) \ln {\frac y{1-y}}=W^Tx+b \tag{7} ln1−yy=WTx+b(7) It can be seen that (7) and (4) Very similar , At the same time, if y y y As a sample x x x The possibility of taking a positive example , be 1 − y 1-y 1−y As a counterexample , The ratio of the two is called probability , This is why the model is called log probability regression . This method has many advantages , The first is to model the possibility of classification directly , There is no need to assume the distribution of data in advance , The problem of inaccurate distribution assumption is avoided , At the same time, it can not only predict categories , Approximate probability predictions can also be obtained , It is helpful for some tasks that use probability to assist decision-making , Last , Its objective function is derivable of any order , It has good mathematical properties .
Linear discriminant analysis (LDA)
LDA The idea is to project a given training set onto a straight line , Make the projection points of similar samples as close as possible , The projection points of heterogeneous samples are as far as possible . When classifying new samples , Project it onto this line , According to the position of the projection point to determine the new sample category .
LDA The goal of maximization is the generalized Rayleigh quotient of the inter class divergence matrix and the intra class divergence matrix , meanwhile , If the use of LDA Project the sample into a new space , Its dimension usually decreases , And the projection process uses category information , therefore LDA It is also regarded as a classical supervised dimensionality reduction technique .
Multi category learning
Multi classification learning can directly extend the method of two classification to multi classification , But more often , Based on some basic strategies , Using the two class learner to solve the multi class problem . The basic idea is “ The dismantling method ”, Split the original problem into multiple binary tasks , Finally, the prediction results are integrated , So as to obtain the results of multi classification . The most classic split strategy is one-to-one (OVO)、 A couple of the rest (OVR) And many to many (MVM).
OVO The strategy is to N Pairing two categories , The resulting N ∗ ( N − 1 ) 2 \frac{N*(N-1)}{2} 2N∗(N−1) Two sub tasks , In the test phase , New samples will be submitted to all classifiers at the same time , The resulting N ∗ ( N − 1 ) 2 \frac{N*(N-1)}{2} 2N∗(N−1) results , Then use the vote , Take the most predicted category as the final classification result .
OVR The strategy is to take an example of a class as a positive example , Examples of other classes are used as counterexamples to train N A classifier , At testing time , If only one classifier has a positive prediction result , The result is the final classification result , If there are multiple classifiers, we need to consider the confidence of each classifier , Select the category mark with high confidence as the classification result . For example, one person guesses the number ,5 Judges (5 A classifier ), Each judge can only answer whether the number guessed by the contestant is right or wrong , When two judges clash , You need to consider which judge is the most reliable ( High confidence ).
MVM The policy treats several classes as positive classes at a time , The rest of the classes are anti classes . The design of positive and negative classes needs to be designed , Most commonly used MVM The technology is “ Error correcting output code ”, By coding 、 The decoding operation returns the final prediction result .
The category of multi classification learning refers to the category of samples , Each sample belongs to only one category . If a sample has multiple labels ( Category ) It is called multi tag learning .
Category imbalance
Category imbalance refers to the situation that the number of training samples in different categories varies greatly in the classification task . Than you have 99 A good example ,1 A counterexample , The classifier only needs to output all positive examples, and the accuracy can reach 99%, But this kind of classifier is useless .
Solutions to class imbalance :
(1) Zoom again . Usually , We will output the classifier y With a threshold (0.5) The comparison , For example, greater than 0.5 Is a positive example , Less than 0.5 Is a counterexample , That is, the output is the possibility that the sample belongs to positive and negative examples ,0.5 It means that the default positive and negative examples are the same , Actually it's not right , Therefore, the predicted value needs to be adjusted , This method of adjustment is called rescaling . But the premise of this operation is that the training sample is the unbiased sampling of the real sample , This assumption usually doesn't hold .
(2) Undersampling . That is, remove some samples to make the number of positive and negative examples close to . Under sampling may lose some important information .
(3) Oversampling . That is, add some samples to make the number of positive and negative examples close to . You can't simply copy , Otherwise, over fitting will occur .
边栏推荐
- QT adds a summary of the problems encountered in the QObject class (you want to use signals and slots) and solves them in person. Error: undefined reference to `vtable for xxxxx (your class name)‘
- The second regular match is inconsistent with the first one, and the match in the regular loop is invalid
- 7-5 复数四则运算
- 视频分类的类间和类内关系——正则化
- Design of tablewithpage
- Process creation and recycling
- Judge whether the network file exists, obtain the network file size, creation time and modification time
- Channel Shuffle类
- K52. Chapter 1: installing kubernetes v1.22 based on kubeadm -- cluster deployment
- Byte order - how to judge the big end and the small end
猜你喜欢
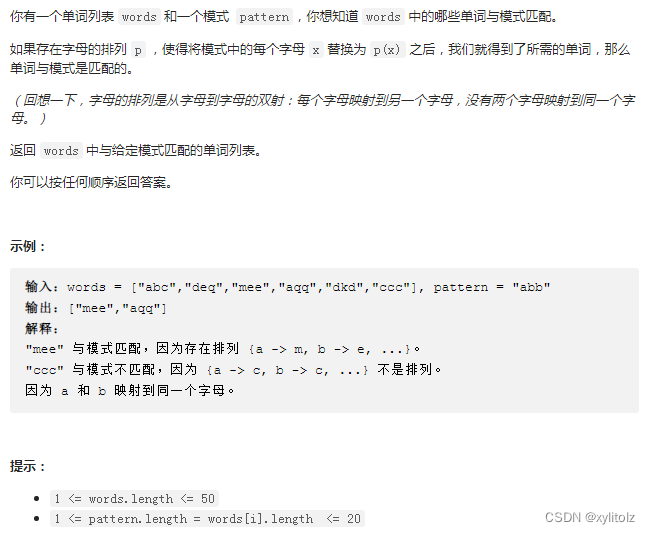
LeetCode 890. 查找和替换模式(模拟+双哈希表)

Cookie和Session
![[foundation of deep learning] back propagation method (1)](/img/0b/540c1f94712a381cae4d30ed624778.png)
[foundation of deep learning] back propagation method (1)

Reentrantlock source code analysis

QT adds a summary of the problems encountered in the QObject class (you want to use signals and slots) and solves them in person. Error: undefined reference to `vtable for xxxxx (your class name)‘

ARM处理器模式与寄存器

Video JS library uses custom components

【深度学习基础】反向传播法(1)

QML学习 第二天
![[foundation of deep learning] learning of neural network (4)](/img/8d/0e1b5d449afa583a52857b9ec7af40.png)
[foundation of deep learning] learning of neural network (4)
随机推荐
Summary of rosbridge use cases_ Chapter 26 opening multiple rosbridge service listening ports on the same server
Judge whether the network file exists, obtain the network file size, creation time and modification time
异步路径处理
[foundation of deep learning] back propagation method (1)
5G NR協議學習--TS38.211下行通道
ARM指令集之数据处理类指令
ARM指令集之Load/Store访存指令(一)
UML series articles (30) architecture modeling -- product diagram
Process creation and recycling
The second regular match is inconsistent with the first one, and the match in the regular loop is invalid
ARM指令集之Load/Store指令寻址方式(二)
Naming specification / annotation specification / logical specification
Multiplication instruction of arm instruction set
The first thing with a server
ARM指令集之数据处理指令寻址方式
LeetCode 497. 非重叠矩形中的随机点(前缀和+二分)
Miscellaneous instructions of arm instruction set
ARM指令集之批量Load/Store指令
Doris records service interface calls
Architecture training module 7