当前位置:网站首页>信息学奥赛一本通(1259:【例9.3】求最长不下降序列)
信息学奥赛一本通(1259:【例9.3】求最长不下降序列)
2022-08-02 20:02:00 【橙子教师】
1259:【例9.3】求最长不下降序列
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 22932 通过数: 8116 Special Judge
【题目描述】
设有由n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)若存在i1<i2<i3<…<ie且有b(i1)<=b(i2)<=…<=b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为7的不下降序列,同时也有7 ,9,16,18,19,21,22,63组成的长度为8的不下降序列。
【输入】
第一行为n,第二行为用空格隔开的n个整数。
【输出】
第一行为输出最大个数max(形式见样例);
第二行为max个整数形成的不下降序列,答案可能不唯一,输出一种就可以了,本题进行特殊评测。
【输入样例】
14
13 7 9 16 38 24 37 18 44 19 21 22 63 15【输出样例】
max=8
7 9 16 18 19 21 22 63【分析】
根据动态规划的原理,由后往前进行搜索(当然从前往后也一样)。
(1)对a[n]来说,由于它是最后一个数,所以当从 a[n]开始查找时,只存在长度为1的不下降序列;
(2)若从a[n-1]开始查找,则存在下面的两种可能性∶
①若a[n-1]<a[n],则存在长度为2的不下降序列a[n-1],a[n]。
②若a[n-1]>a[n],则存在长度为1的不下降序列a[n-1]或a[n]。
(3)一般若从a[i]开始,此时最长不下降序列应该按下列方法求出:
在a[i+1],a[i+2],…,a[n]中,找出一个比 a[i]大的且最长的不下降序列,作为它的后继。
【数据结构】
为算法上的需要,定义三个整型数组(也可以定义一个整数类型二维数组b[n][3])
(1)a[i]:表示第 i 个数的数值本身。
(2)f[i]:表示从 i 位置到达n的最长不下降序列长度。
(3)p[i]:表示从 i 位置开始最长不下降序列的下一个位置,若p[i]=0,则表示后面没有连接项。
【动规分析】
(1)划分阶段。
阶段:根据p数组,即最长不下降序列的位置来划分阶段。
(2)确定状态和状态变量。
状态:f 数组的中值表示从第 i 位置到达 n 的最长不下降长度,都是不同的状态,状态信息用f[i]表示。
(2)确定决策并写出状态转移方程。
f[i]的值从哪来?当然是从f[j]而来,i<j≤n,策略:不下降,即a[i]≤a[j]。故:
状态转移方程: f[i]=max{ f[j]+1 | i<j≤n, a[i]≤a[j] }。
(4)寻找边界条件。
边界:f[n]=1,p[n]=0。
(5)设计并实现程序,数据存储和问题求解过程如下:

【参考代码】
#include <stdio.h>
#define MAXN 210
int a[MAXN]; //数据存储数组
int f[MAXN]; //最长不下降子序列数组,f[i]表示从i位置到达n的最长不下降序列长度
int p[MAXN]; //位置数组,从i位置开始最长不下降序列的下一个位置
int main()
{
int i,j;
int n; //数列长度
int maxn; //以某数为起点的最长不降序列
int k;
int ans=0; //最终结果
int s; //s起始位置
scanf("%d",&n);
for(i=1;i<=n;i++) //输入序列的初始值
scanf("%d",&a[i]);
f[n]=1;
p[n]=0;
for(i=n-1;i>=1;i--) //逆序求最长不下降序列
{
maxn=0;
k=0;
for(j=i+1;j<=n;j++)
{
if(a[i]<=a[j] && f[j]>maxn)
{
maxn=f[j];
k=j;
}
}
if(maxn>=0)
{
f[i]=maxn+1;
p[i]=k;
}
}
for(i=1;i<=n;i++) //求最长不下降序列起始位置
{
if(f[i]>ans)
{
ans=f[i];
s=i;
}
}
printf("max=%d\n",ans); //输出结果
while(s!=0) //输出最长不下降序列
{
printf("%d ",a[s]);
s=p[s];
}
return 0;
}边栏推荐
- 特拉维夫大学 | Efficient Long-Text Understanding with Short-Text Models(使用短文本模型进行高效的长文本理解)
- Kali命令ifconfig报错command not found
- VMware虚拟机无法上网
- 解析List接口中的常用的被实现子类重写的方法
- Caldera(一)配置完成的虚拟机镜像及admin身份简单使用
- arm64麒麟安装paddlehub(国产化)
- EasyExcel dynamic parsing and save table columns
- 银保监会:人身险产品信披材料应由保险公司总公司统一负责管理
- 「面试必会」这应该是最有深度的TCP三次握手、四次挥手细节讲解
- pytorch的tensor创建和操作记录
猜你喜欢
![[安洵杯 2019]easy_web](/img/26/c04bc8b9c65ac75ddd2696b48e1661.png)
[安洵杯 2019]easy_web
Parse common methods in the Collection interface that are overridden by subclasses
The time series database has been developed for 5 years. What problem does it need to solve?
遇上Mysql亿级优化,怎么办

OpenCV开发中的内存管理问题

SCANIA SCANIA OTL tag is introduced
SQL Server实现group_concat功能
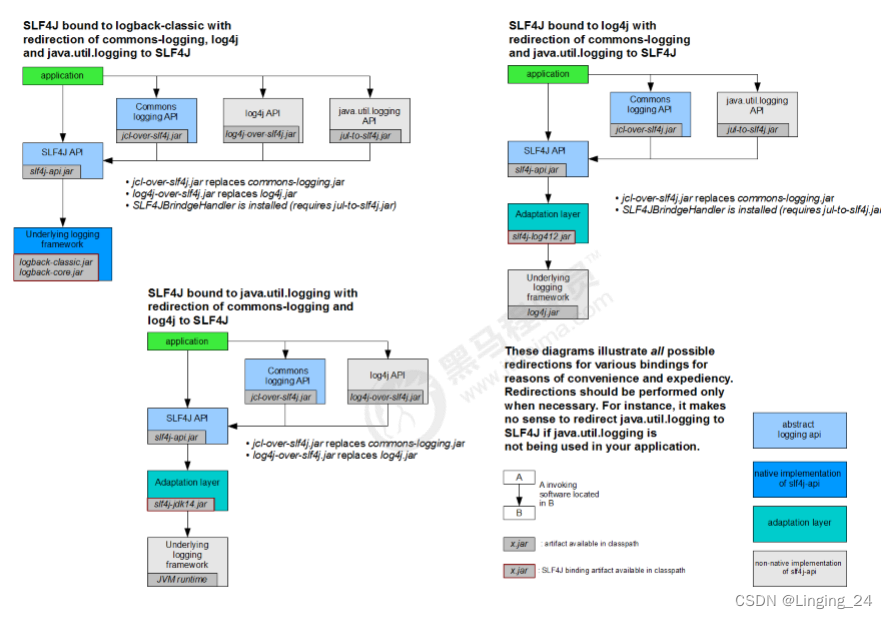
日志框架学习
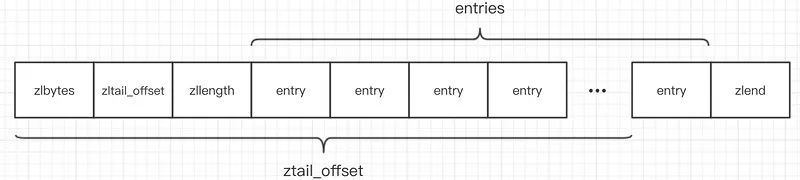
Five data structures of Redis and their corresponding usage scenarios
GNN教程:图神经网络基础知识!
随机推荐
Triacetin是什么化学材料
Wintun:一款惊艳的 WireGuard 虚拟网卡接口驱动
PG's SQL execution plan
【软件工程导论】软件工程导论笔记
golang源码分析之geoip2-golang
Solve the docker mysql can't write Chinese
golang源码分析:time/rate
Likou Question of the Day - Day 46 - 344. Reverse Strings
二丙二醇甲醚醋酸酯
牛客题目——滑动窗口的最大值、矩阵最长递增路径、顺时针旋转矩阵、接雨水问题
GNN教程:图神经网络基础知识!
技术分享 | Apache Linkis 快速集成网页IDE工具 Scriptis
【LeetCode】622. 设计循环队列
奥特学园ROS笔记--7(289-325节)
云平台简介
What is a Field Service Management System (FSM)?what is the benefit?
广东省数字经济发展指引 1.0之建成数据安全保障体系
第一次进入前20名
Helm基础知识
VMware虚拟机无法上网
