当前位置:网站首页>牛客网刷题(二)
牛客网刷题(二)
2022-07-31 15:59:00 【std i hurt o love】
二叉树根节点到叶子节点的所有路径和
题目:二叉树根节点到叶子节点的所有路径和
描述:给定一个仅包含数字0−9的二叉树,每一条从根节点到叶子节点的路径都可以用一个数字表示。例如根节点到叶子节点的一条路径是1→2→3,那么这条路径就用123来代替。
找出根节点到叶子节点的所有路径表示的数字之和
例如:这颗二叉树一共有两条路径,根节点到叶子节点的路径1→2用数字12代替,根节点到叶子节点的路径1→3用数字13代替,所以答案为12+13=25。
示例1:输入:{1,0},返回值:10
解法一:
思路分析:通过题目分析,我们可以将每条根节点到叶子结点的路径和用一个数字代替,如果向下一个结点,就将之前的数字都左移一位,通过使用dfs找到左右子树的所有路径,最后回溯求和,得到最后的结果值。
/** * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
class Solution {
public:
/** * * @param root TreeNode类 * @return int整型 */
int sumNumbers(TreeNode* root) {
// write code here
if(!root)//特殊情况
return 0;
int sum = 0;
return preorder(root, sum);
}
int preorder(TreeNode* root, int sum){
if(root == NULL)
return 0;
sum = sum * 10 + root->val;//一层一层进行遍历
if(!root->left && !root->right)//没有子结点
return sum;
return preorder(root->left, sum) + preorder(root->right, sum);
}
};
递归遍历二叉树中的结点,其时间复杂度为O(N),空间复杂度为O(1)。
解法二:
思路分析:我们也可以通过在vector中保存路径来计算结果,将根节点到叶子节点的路径记录到paths中,通过计算得到最终的结果。
/** * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
class Solution {
public:
/** * * @param root TreeNode类 * @return int整型 */
int sumNumbers(TreeNode* root) {
// 通过在vector中保存路径来计算结果
if(root == nullptr)
return 0;
vector temp;
vector paths;
path(temp, root, paths);
//对paths里记录的内容进行求和
int sum = 0; //最终结果
for(auto &i : paths){
int line = 0; //记录单个路径的和
for(auto &j : i){
line = line*10+j;
}
sum += line;
}
return sum;
}
void path(vector&temp, TreeNode* root, vector &paths){
if(root == nullptr)
return;
temp.push_back(root->val);
if(root->left==nullptr && root->right==nullptr)
paths.push_back(temp); //将根节点到叶子节点的一个路径记录到paths中
if(root->left)
path(temp, root->left, paths);
if(root->right)
path(temp, root->right, paths);
temp.pop_back();
}
};
通过 vector中保存路径来计算结果,要循环计算单个路径的和,所以其时间复杂度最大为O(N),空间复杂度为O(N)。
二、二叉树中的最大路径和
这个题目我们需要计算出一棵二叉树上面的所有的路径当中,找出路径的和最大的那个值。
这个题目的难点就是中途可能会存在权值为负数的情况,还有权值为0的情况不好处理。
这个题目还是有点意思的,我们可以用一个类似与树形DP的方法进行求解。
前缀知识,树形DP,树形DP就是我们假设我们知道了一棵二叉树的左右的子节点的最优值,然后我们可以传递到这个节点本身,最终传递到整棵树上面。
解法一 DFS+树形DP
对于树的题目,很大程度上都可以使用搜索进行求解。这个题目也是一样的,使用一个先序遍历的思想,当我们进行递归的时候,我们先向左右子节点进行递归,求出左右子树的最优的情况返回,然后我们就可以更新这个节点的最优的情况了。
结合下面的图我们可以更好地理解我们如何进行递归。
/** * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
class Solution {
public:
/** * * @param root TreeNode类 * @return int整型 */
// 注意,可能会存在权值为负数的节点,所以把这个先设置为负无穷
int ans=-0x3f3f3f3f;
int DFS(TreeNode* now){
// 这个是一个叶子节点
if(!now) return 0;
// 递归求出左右子树的最大的路径值
int left=DFS(now->left);
int right=DFS(now->right);
int nowSum=now->val;
if(left>0) nowSum+=left;
if(right>0) nowSum+=right;
// 更新这个节点,这条路径是这个节点的左右子树包括这个节点本身构成的
ans=max(ans,nowSum);
// 向上传递的时候只能三种方式进行传递
// 左+中,右+中,中这三种方法
return max(now->val,max(left,right)+now->val);
}
int maxPathSum(TreeNode* root) {
// write code here
ans=max(ans,DFS(root));
return ans;
}
};
解法二:BFS
和上面的DFS的思路一样,我们使用BFS进行求解,我们可以使用队列来进行一个层序遍历。我们先把这些结果都放到一个动态数组里面,然后我们从后往前面开始进行遍历,这其实就是我们从叶子节点到根节点开始进行访问,模拟了一个树形DP的一个过程。不断从叶子节点更新到根节点的,维护最终的答案。
代码如下
在进行BFS的时候可能存在遍历到所有的结点的信息的情况,时间复杂度为O(n)
需要对所有的结点的信息进行存储,空间复杂度为O(n)
/** * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
class Solution {
public:
/** * * @param root TreeNode类 * @return int整型 */
vector<TreeNode*> node;
int ans=-0x3f3f3f3f;
queue<TreeNode*> q;
int maxPathSum(TreeNode* root) {
// write code here
if(!root){
return 0;
}
q.push(root);
// 进行一个层序遍历求出从根节点到叶子节点的所有节点
while(!q.empty()){
TreeNode* now=q.front();
q.pop();
node.push_back(now);
if(now->left) q.push(now->left);
if(now->right) q.push(now->right);
}
// 从后往前开始遍历
for(int i=node.size()-1;i>=0;i--){
TreeNode* now=node[i];
// 如果这个是叶子节点,那么直接比较
if(now->left==NULL&&now->right==NULL){
ans=max(ans,now->val);
}else{
// 不是叶子节点的情况,这个时候我们的左右子节点的最优值已经求出
int left=0,right=0;
if(now->left){
left=now->left->val;
}
if(now->right){
right=now->right->val;
}
int nowSum=now->val;
// 更新这个节点的最优值,要用于向上进行传递
now->val=max(now->val,max(left,right)+nowSum);
// 更新答案
ans=max(ans,max(now->val,left+right+nowSum));
}
}
return ans;
}
};
边栏推荐
- Single-cell sequencing workflow (single-cell RNA sequencing)
- After the form is submitted, the page does not jump [easy to understand]
- Replication Latency Case (3) - Monotonic Read
- 单细胞测序流程(单细胞rna测序)
- Insert into data table to insert data
- Premiere Pro 2022 for (pr 2022)v22.5.0
- 多主复制的适用场景(2)-需离线操作的客户端和协作编辑
- 复杂高维医学数据挖掘与疾病风险分类研究
- 2022年必读的12本机器学习书籍推荐
- ML.NET related resources
猜你喜欢
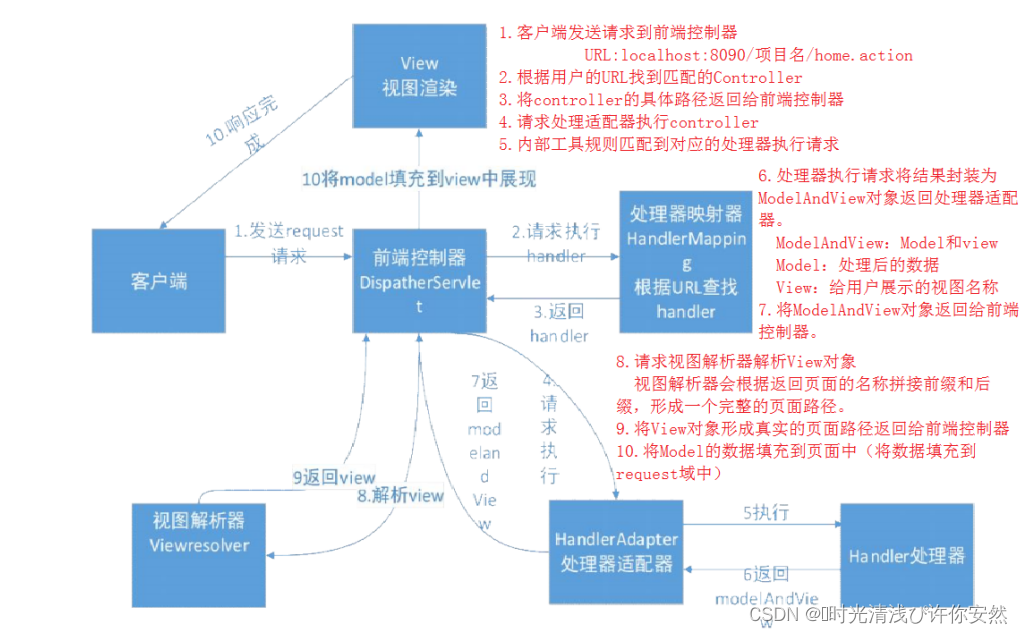
SringMVC中个常见的几个问题

T - sne + data visualization parts of the network parameters

gerrit中如何切换远程服务器

对话庄表伟:开源第一课
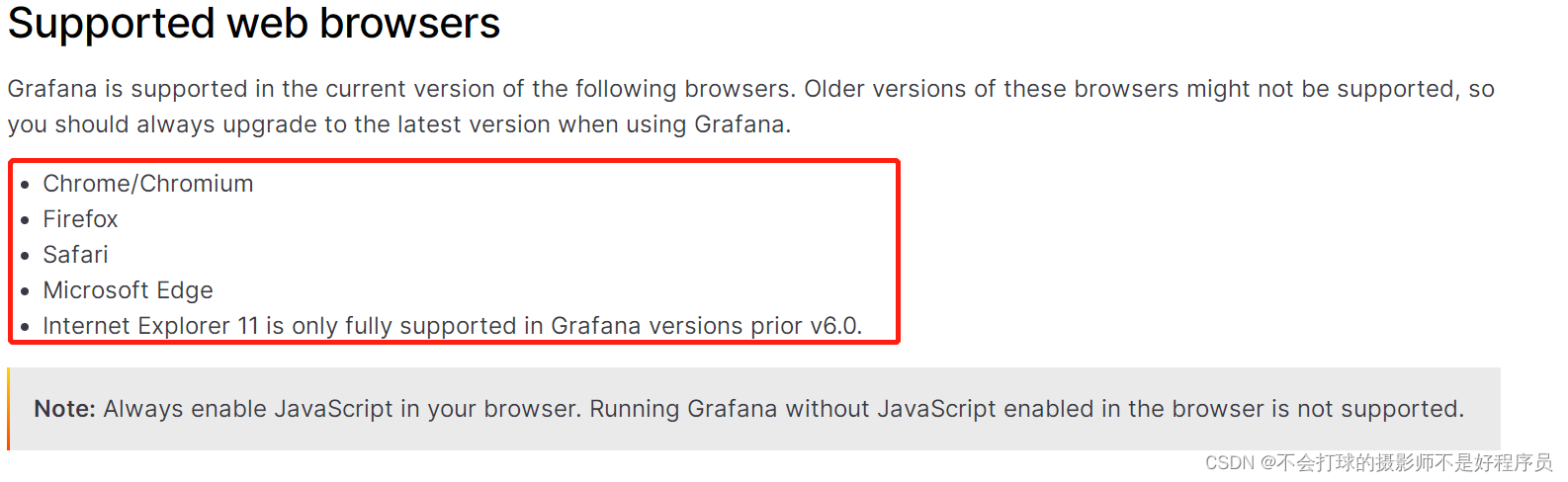
After Grafana is installed, the web opens and reports an error
腾讯云部署----DevOps
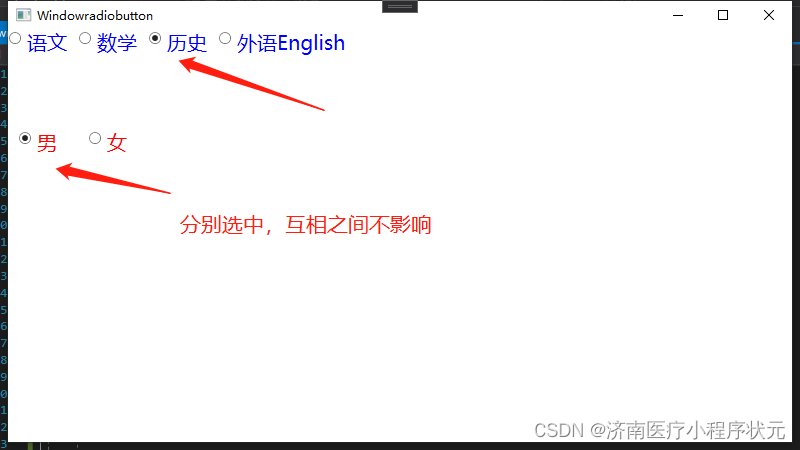
radiobutton的使用
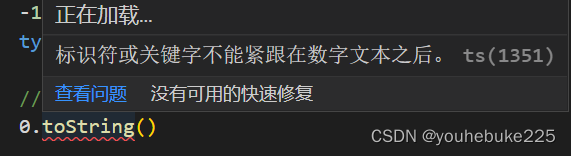
js的toString方法

Unity 之 图集属性详解和代码示例 -- 拓展一键自动打包图集工具
![[Meetup Preview] OpenMLDB+OneFlow: Link feature engineering to model training to accelerate machine learning model development](/img/f6/311d5a4c70993df6291250d2025d3f.jpg)
[Meetup Preview] OpenMLDB+OneFlow: Link feature engineering to model training to accelerate machine learning model development
随机推荐
mysql黑窗口~建库建表
【TypeScript】深入学习TypeScript类型操作
Design and Implementation of Compiler Based on C Language
Delete the disk in good condition (recovery partition)
外媒所言非虚,苹果降价或许是真的在清库存
6-22漏洞利用-postgresql数据库密码破解
Premiere Pro 2022 for (pr 2022)v22.5.0
ML.NET相关资源整理
"Autumn Recruitment Series" MySQL Interview Core 25 Questions (with answers)
js的toString方法
Visualize GraphQL schemas with GraphiQL
MySQL database operations
做事软件开发-法的重要性所在以及合理结论的认识
TypeError: unhashable type: ‘list‘
Kubernetes common commands
多主复制下处理写冲突(4)-多主复制拓扑
Single-cell sequencing workflow (single-cell RNA sequencing)
MySQL数据库操作
what exactly is json (c# json)
The new BMW 3 Series is on the market, with safety and comfort