当前位置:网站首页>2161. divide the array according to the given number
2161. divide the array according to the given number
2022-06-11 09:14:00 【Mr Gao】
2161. Divide the array according to the given number
I'll give you a subscript from 0 The starting array of integers nums And an integer pivot . Would you please nums Rearrange , Make the following conditions true :
All less than pivot All elements greater than pivot The elements of Before .
All equal to pivot All elements appear in less than and greater than pivot The elements of middle .
Less than pivot Between elements of and greater than pivot Between elements of Relative order No change .
More formal , Consider each pair pi,pj ,pi Is the initial position i The new location of the element ,pj Is the initial position j The new location of the element . For less than pivot The elements of , If i < j And nums[i] < pivot and nums[j] < pivot All set up , that pi < pj It was also established . Allied , For greater than pivot The elements of , If i < j And nums[i] > pivot and nums[j] > pivot All set up , that pi < pj .
Please go back and rearrange nums The result array after the array .
Example 1:
Input :nums = [9,12,5,10,14,3,10], pivot = 10
Output :[9,5,3,10,10,12,14]
explain :
Elements 9 ,5 and 3 Less than pivot , So they're on the far left of the array .
Elements 12 and 14 Greater than pivot , So they're on the far right of the array .
Less than pivot The relative position sum of the elements of is greater than pivot The relative positions of the elements are [9, 5, 3] and [12, 14] , Their relative order in the result array needs to be preserved .
Example 2:
Input :nums = [-3,4,3,2], pivot = 2
Output :[-3,2,4,3]
explain :
Elements -3 Less than pivot , So on the far left of the array .
Elements 4 and 3 Greater than pivot , So they're on the far right of the array .
Less than pivot The relative position sum of the elements of is greater than pivot The relative positions of the elements are [-3] and [4, 3] , Their relative order in the result array needs to be preserved .
This question , We can set up a 2*numsize Array of , It can solve the problem well without changing the position
The solution code is as follows :
/** * Note: The returned array must be malloced, assume caller calls free(). */
int* pivotArray(int* nums, int numsSize, int pivot, int* returnSize){
int *numst=(int *)malloc(sizeof(int)*numsSize*2);
int epo=numsSize;
int max=numsSize*2-1;
int i=0;
for(i;i<numsSize*2;i++){
if(i<numsSize){
numst[i]=nums[i];
}
else{
numst[i]=-59789;
}
}
for(i=numsSize-1;i>=0;i--){
if(nums[i]>pivot){
numst[max--]=nums[i];
numst[i]=-59789;
}
if(nums[i]==pivot){
numst[epo++]=nums[i];
numst[i]=-59789;
}
}
int po=0;
for(i=0;i<numsSize*2;i++){
if(numst[i]!=-59789){
numst[po++]=numst[i];
}
}
*returnSize=numsSize;
return numst;
}
边栏推荐
- [scheme design] scheme of household oximeter based on single chip microcomputer
- MySQL啟動報錯“Bind on TCP/IP port: Address already in use”
- Clothing ERP: how do enterprises carry out implementation planning?
- 2130. maximum twin sum of linked list
- [C language - function stack frame] analyze the whole process of function call from the perspective of disassembly
- 【237. 删除链表中的节点】
- 制作业信息化为什么难施行?
- 工厂出产流程中的这些问题,应该怎么处理?
- Design of wrist sphygmomanometer based on sic32f911ret6
- Machine learning notes - in depth Learning Skills Checklist
猜你喜欢

Openstack explanation (22) -- neutron plug-in configuration

Console you don't know

Openstack explanation (XXIII) -- other configurations, database initialization and service startup of neutron
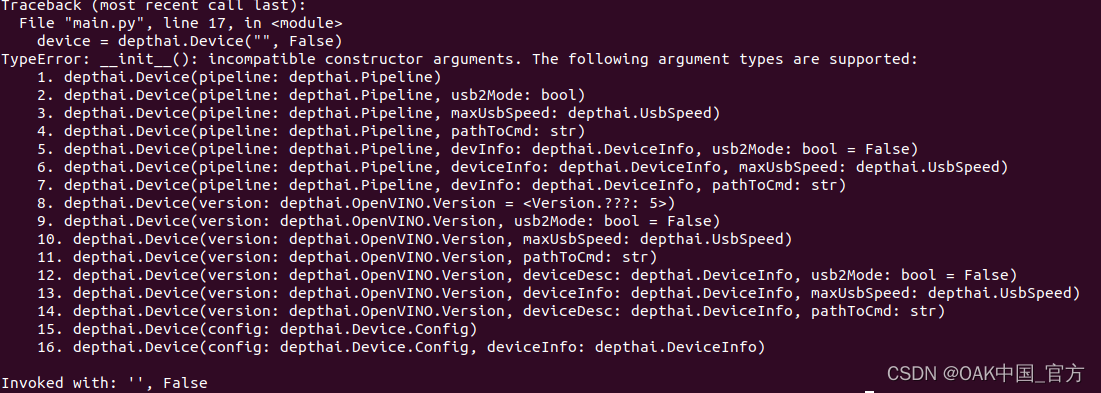
报错device = depthai.Device(““, False) TypeError: _init_(): incompatible constructor arguments.

OpenCV CEO教你用OAK(四):创建复杂的管道

openstack详解(二十二)——Neutron插件配置

Install jupyter in the specified environment

Shandong University project training (IV) -- wechat applet scans web QR code to realize web login

报错Version mismatch between installed depthai lib and the required one by the scrip.

Openstack explanation (21) -- installation and configuration of neutron components
随机推荐
844. 比较含退格的字符串
ArcGIS 10.9.1 geological and meteorological volume metadata processing and service publishing and calling
2130. maximum twin sum of linked list
206. 反转链表
Fabric.js 動態設置字號大小
Why is it difficult to implement informatization in manufacturing industry?
multiplication table
[scheme development] sphygmomanometer scheme pressure sensor sic160
20. 有效的括号
openstack详解(二十四)——Neutron服务注册
自动化运维文章大合集
Kubelet error getting node help
Pulsar job Plaza | Tencent, Huawei cloud, shrimp skin, Zhong'an insurance, streamnational and other hot jobs
报错ModularNotFoundError: No module named ‘find_version’
ERP体系的这些优势,你知道吗?
206. 反转链表
206. reverse linked list
OpenCV OAK相机对比及介绍
Pytorch installation for getting started with deep learning
Error [detectionnetwork (1)][warning]network compiled for 6 shapes, maximum available 10, compiling for 5 S