当前位置:网站首页>(Codeforce 757)E. Bash Plays with Functions(积性函数)
(Codeforce 757)E. Bash Plays with Functions(积性函数)
2022-08-01 04:47:00 【AC__dream】
题目:
样例输入:
5
0 30
1 25
3 65
2 5
4 48
样例输出:
8
5
25
4
630
题意:
我们先来分析r=0的情况,假如我们现在求f0(n),n=p1^a1*p2^a2*……*pm^am
那么f0(n)就等于2^m,这是显然的,因为我们假设p=p1^b1*p2^b2*……*pm^bm,那么对于任意的bi(1<=i<=m)都有bi=0或者bi=ai,要不然不会存在q使得p*q=n且gcd(p,q)=1,那么我们就不难发现其实f0(x)是一个积性函数。假设对于n=p*q,gcd(p,q)=1,则p和q的质因子分解中不会存在相同质因子,不妨假设p有i个质因子,q有j个质因子,那么p*q就会有i+j个质因子,那么f0(pq)=2^(i+j)=2^i*2^j=f0(p)*f0(q),所以f0(x)是一个积性函数。
下面我用归纳法来证明对于任意的r都有fr(x)是一个积性函数。

我们知道对于r=0的情况f0(n)的值只与n的质因子的种类有关,而与具体的质因子无关,而r不为0的情况是由r=0的情况得到的,所以r不为0的时候与具体的质因子也不会有关系。我们上面推导了对于任意的r都有fr(x)是一个积性函数,所以我们求fr(n)时只需要看n的质因子分解情况即可,那么问题就转变为求解fr(p^i),p是一个质数,根据公式我们可以发现fr(p^i)= ,又因为与具体的质因子无关,通过上式我们可以发现只与质因子的次数有关,那么我们就可以令f[i][j]记录fi(p^j)的值 ,由于n是小于1e6的,所以质因子分解中最高次数不会超过20,这样通过O(r*20)就可以预处理出来所有的数。当r=0时,根据其定义我们可以知道f[0][1]=1,f[0][i]=2(i>1),预处理一下即可
,又因为与具体的质因子无关,通过上式我们可以发现只与质因子的次数有关,那么我们就可以令f[i][j]记录fi(p^j)的值 ,由于n是小于1e6的,所以质因子分解中最高次数不会超过20,这样通过O(r*20)就可以预处理出来所有的数。当r=0时,根据其定义我们可以知道f[0][1]=1,f[0][i]=2(i>1),预处理一下即可
剩下的就是对于每组询问记录一下质因子次数,直接利用积性函数性质求解了。
下面是代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e6+10,mod=1e9+7;
long long f[N][21];//f[i][j]表示fi(p^j)
int prime[N],tt;
bool vis[N];
void init()
{
f[0][0]=1;
for(int i=1;i<=20;i++) f[0][i]=2;
for(int i=1;i<=1000000;i++)
{
long long ans=0;
for(int j=0;j<=20;j++)
{
ans=(ans+f[i-1][j])%mod;
f[i][j]=ans;
}
}
}
int main()
{
init();
int T;
cin>>T;
while(T--)
{
int r,n;
scanf("%d%d",&r,&n);
long long ans=1;
for(int i=2;i*i<=n;i++)
{
int cnt=0;
if(n%i==0)
{
while(n%i==0)
{
n/=i;
cnt++;
}
ans=ans*f[r][cnt]%mod;
}
}
if(n>1) ans=ans*f[r][1]%mod;
printf("%lld\n",ans);
}
return 0;
}
边栏推荐
- Input input box cursor automatically jumps to the last bug after the previous input
- Progressive Reconstruction of Visual Structure for Image Inpainting 论文笔记
- IJCAI2022 | Hybrid Probabilistic Reasoning with Algebraic and Logical Constraints
- PMP 80个输入输出总结
- 56:第五章:开发admin管理服务:9:开发【文件上传到,MongoDB的GridFS中,接口】;(把文件上传到GridFS的SOP)
- 认真对待每一个时刻
- button remove black frame
- MySQL-数据定义语言-DDLdatebase define language
- SQL Analysis of ShardingSphere
- The Principle Of Percona Toolkit Nibble Algorithm
猜你喜欢

Make your Lottie support word wrapping in text fields
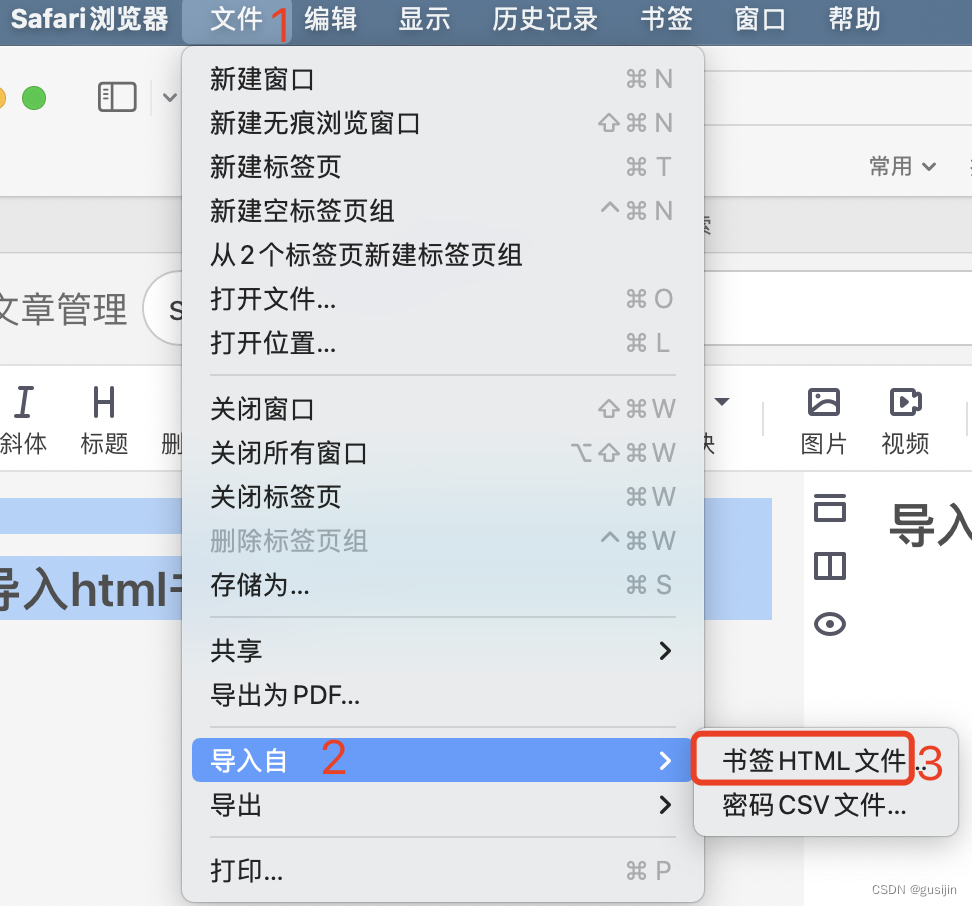
safari浏览器怎么导入书签
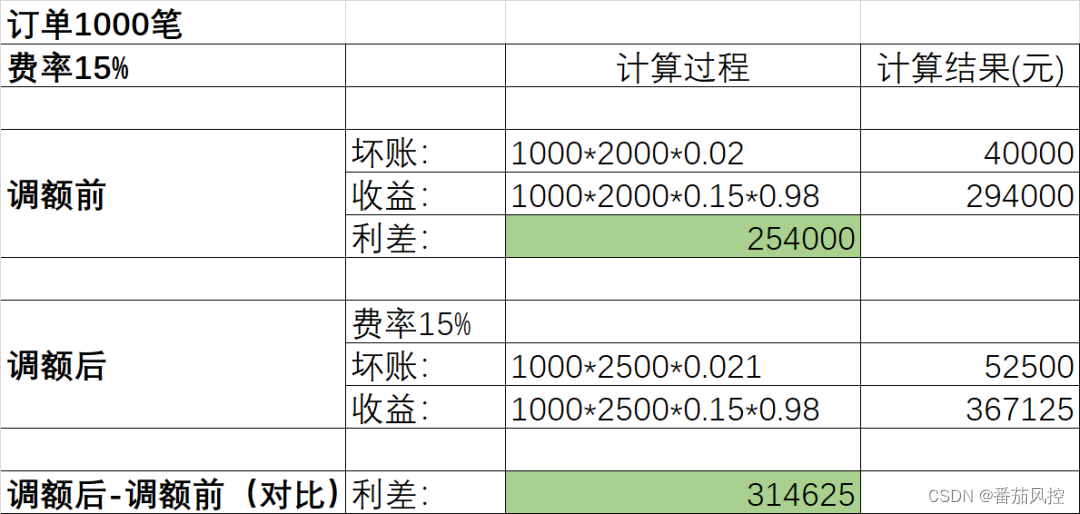
Risk strategy important steps of tuning method

typescript21 - Comparison of Interfaces and Type Aliases
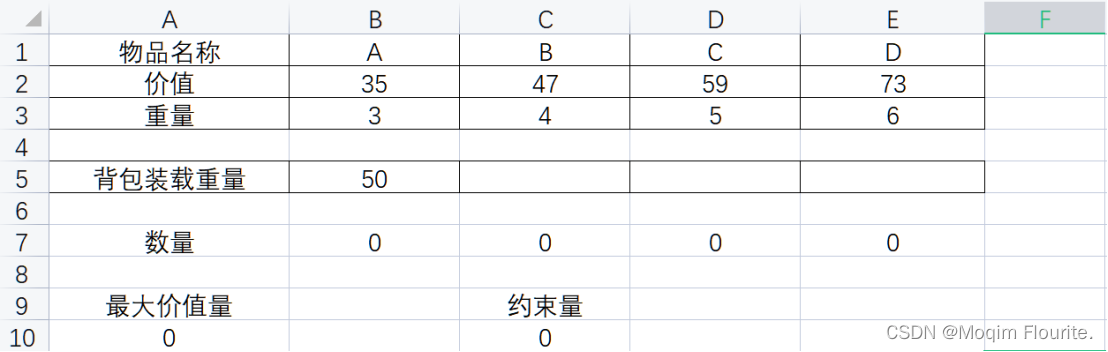
Excel record of integer programming optimization model to solve the problem

The method of solving stored procedure table name passing through variable in mysql

Optional parameters typescript19 - object

Software Testing Interview (3)
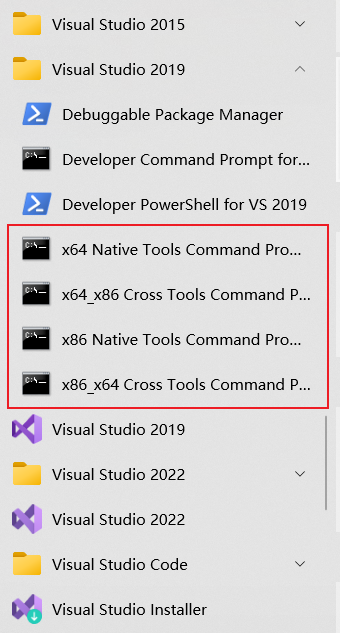
Visual Studio提供的 Command Prompt 到底有啥用

【目标检测】YOLOv7理论简介+实践测试
随机推荐
微软 Win10 照片磁贴后的又一“刺客”,谷歌 Chrome 浏览器将在新标签页展示用户照片
MySQL-数据定义语言-DDLdatebase define language
PMP子过程定义总结
【愚公系列】2022年07月 Go教学课程 024-函数
智芯传感输液泵压力传感器 为精准智能控制注入科技“强心剂”
Error using ts-node
typescript27 - what about enumeration types
基于STM32设计的UNO卡牌游戏(双人、多人对战)
Risk strategy important steps of tuning method
PMP 项目资源管理
请问shake数据库中为什么读取100个collection 后,直接就退出了,不继续读了呢?
Hackers can how bad to what degree?
时时刻刻保持敬畏之心
Character encoding and floating point calculation precision loss problem
「以云为核,无感极速」顶象第五代验证码
在沈自所的半年总结
Lawyer Interpretation | Guns or Roses?Talking about Metaverse Interoperability from the Battle of Big Manufacturers
IJCAI2022 | Hybrid Probabilistic Reasoning with Algebraic and Logical Constraints
API设计笔记:pimpl技巧
Game Theory (Depu) and Sun Tzu's Art of War (42/100)