当前位置:网站首页>C # realizes FFT forward and inverse transformation and frequency domain filtering
C # realizes FFT forward and inverse transformation and frequency domain filtering
2022-07-04 16:39:00 【Full stack programmer webmaster】
To carry out FFT The first operation is to construct complex classes , Reference resources
http://blog.csdn.net/iamoyjj/archive/2009/05/15/4190089.aspx
The following program is implemented on the basis of relying on the above complex classes FFT Forward and inverse transform algorithm and frequency domain filtering algorithm , In addition, if it is a real number FFT Words , To put FFT The resulting complex array is converted to a real array , In the following classes Cmp2Mdl The function of method is this . This FFT Algorithm is base -2FFT Algorithm , therefore , If the input sequence must be 2 Of n The power point is long .
The basic principle of frequency domain filtering is :
1、 The input sequence is FFT
2、 The obtained spectrum is multiplied by a weight function ( filter , Transfer function of system )
3、 The results obtained are carried out IFFT
4、 If it is a real number operation, use Cmp2Mdl Method to real number
The code is as follows :
/// <summary>
/// Frequency analyzer
/// </summary>
public static class FreqAnalyzer
{
/// <summary>
/// Find the complex number complex Module of array modul Array
/// </summary>
/// <param name=”input”> A complex array </param>
/// <returns> Module group </returns>
public static double[] Cmp2Mdl(Complex[] input)
{
/// The length of the input array determines the length of the output array
double[] output = new double[input.Length];
/// Modulo all input complex numbers
for (int i = 0; i < input.Length; i++)
{
if (input[i].Real > 0)
{
output[i] = -input[i].ToModul();
}
else
{
output[i] = input[i].ToModul();
}
}
/// Return modulo array
return output;
}
/// <summary>
/// Fourier transform or inverse transform , Recursive implementation of multi-level butterfly operation
/// As the output of the inverse transformation, it needs to be divided by the length of the sequence
/// ! Be careful : The sequence length of the input class must be 2^n
/// </summary>
/// <param name=”input”> Input real sequence </param>
/// <param name=”invert”>false= Positive transformation ,true= Reverse transformation </param>
/// <returns> Fourier transform or inverse transform sequence </returns>
public static Complex[] FFT(double[] input, bool invert)
{
/// The length of the output sequence is determined by the input sequence
Complex[] output = new Complex[input.Length];
/// Convert the input real number to complex number
for (int i = 0; i < input.Length; i++)
{
output[i] = new Complex(input[i]);
}
/// return FFT or IFFT The sequence after
return output = FFT(output, invert);
}
/// <summary>
/// Fourier transform or inverse transform , Recursive implementation of multi-level butterfly operation
/// As the output of the inverse transformation, it needs to be divided by the length of the sequence
/// ! Be careful : The sequence length of the input class must be 2^n
/// </summary>
/// <param name=”input”> Complex input sequence </param>
/// <param name=”invert”>false= Positive transformation ,true= Reverse transformation </param>
/// <returns> Fourier transform or inverse transform sequence </returns>
private static Complex[] FFT(Complex[] input, bool invert)
{
/// The input sequence has only one element , Output this element and return
if (input.Length == 1)
{
return new Complex[] { input[0] };
}
/// Enter the length of the sequence
int length = input.Length;
/// Enter half the length of the sequence
int half = length / 2;
/// The length of the input sequence determines the length of the output sequence
Complex[] output = new Complex[length];
/// The cardinality of the positive transformation rotation factor
double fac = -2.0 * Math.PI / length;
/// The cardinality of the inverse transformation rotation factor is the opposite number of the positive transformation
if (invert)
{
fac = -fac;
}
/// Points with even subscripts in the sequence
Complex[] evens = new Complex[half];
for (int i = 0; i < half; i++)
{
evens[i] = input[2 * i];
}
/// Find even points FFT or IFFT Result , Recursive implementation of multi-level butterfly operation
Complex[] evenResult = FFT(evens, invert);
/// Points with odd subscripts in the sequence
Complex[] odds = new Complex[half];
for (int i = 0; i < half; i++)
{
odds[i] = input[2 * i + 1];
}
/// Find even points FFT or IFFT Result , Recursive implementation of multi-level butterfly operation
Complex[] oddResult = FFT(odds, invert);
for (int k = 0; k < half; k++)
{
/// Rotation factor
double fack = fac * k;
/// Butterfly operation
Complex oddPart = oddResult[k] * new Complex(Math.Cos(fack), Math.Sin(fack));
output[k] = evenResult[k] + oddPart;
output[k + half] = evenResult[k] – oddPart;
}
/// return FFT or IFFT Result
return output;
}
/// <summary>
/// Frequency domain filter
/// </summary>
/// <param name=”data”> Data to be filtered </param>
/// <param name=”Nc”> Cut off wave number of filter </param>
/// <param name=”Hd”> The weight function of the filter </param>
/// <returns> Filtered data </returns>
private static double[] FreqFilter(double[] data, int Nc, Complex[] Hd)
{
/// Maximum wave number == Data length
int N = data.Length;
/// Enter data for FFT
Complex[] fData = FreqAnalyzer.FFT(data, false);
/// spectrum shaping
for (int i = 0; i < N; i++)
{
fData[i] = Hd[i] * fData[i];
}
/// Data calculation after filtering IFFT
///! Not divided by data length
fData = FreqAnalyzer.FFT(fData, true);
/// Complex number into module
data = FreqAnalyzer.Cmp2Mdl(fData);
/// Divide by the data length
for (int i = 0; i < N; i++)
{
data[i] = -data[i] / N;
}
/// Return filtered data
return data;
}
}
Publisher : Full stack programmer stack length , Reprint please indicate the source :https://javaforall.cn/110913.html Link to the original text :https://javaforall.cn
边栏推荐
- . Net applications consider x64 generation
- Market trend report, technical innovation and market forecast of taillight components in China
- 165 webmaster online toolbox website source code / hare online tool system v2.2.7 Chinese version
- Stew in disorder
- 多年锤炼,迈向Kata 3.0 !走进开箱即用的安全容器体验之旅| 龙蜥技术
- What is torch NN?
- Unity animation day05
- Sql实现Split
- L1-072 scratch lottery
- What is torch NN?
猜你喜欢

How was MP3 born?
![[hcie TAC] question 5 - 1](/img/e0/1b546de7628695ebed422ae57942e4.jpg)
[hcie TAC] question 5 - 1

Stress, anxiety or depression? Correct diagnosis and retreatment
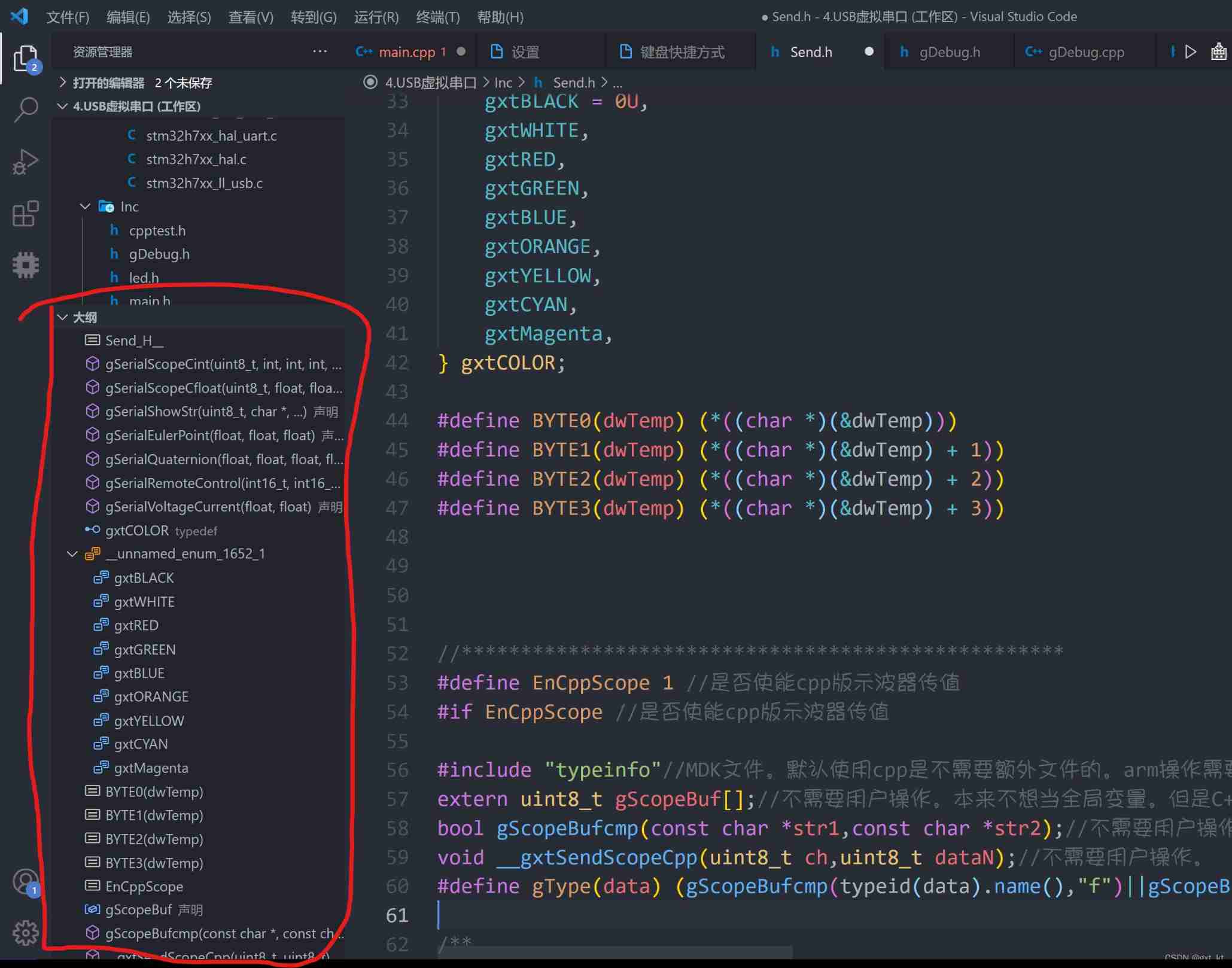
Vscode setting outline shortcut keys to improve efficiency
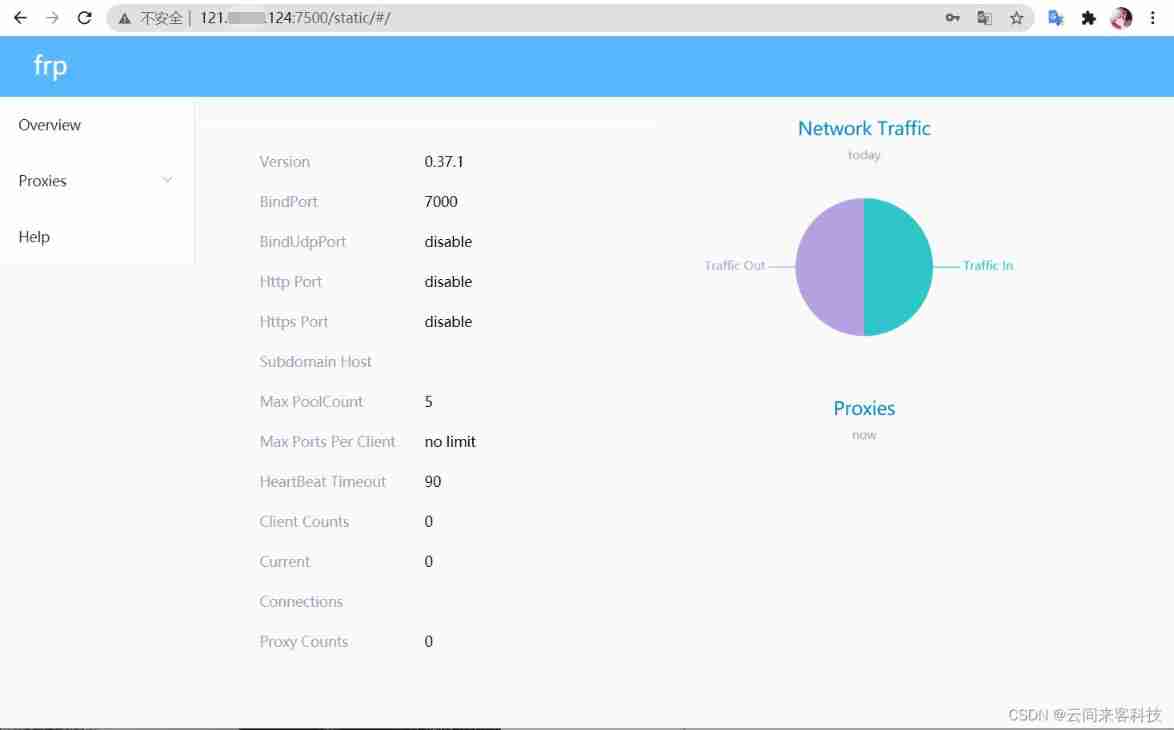
Intranet penetrating FRP: hidden communication tunnel technology

Software Engineer vs Hardware Engineer
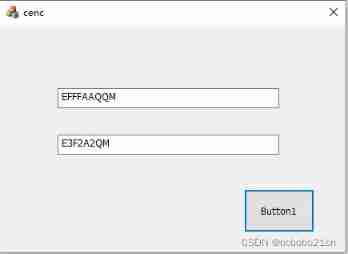
MFC implementation of ACM basic questions encoded by the number of characters
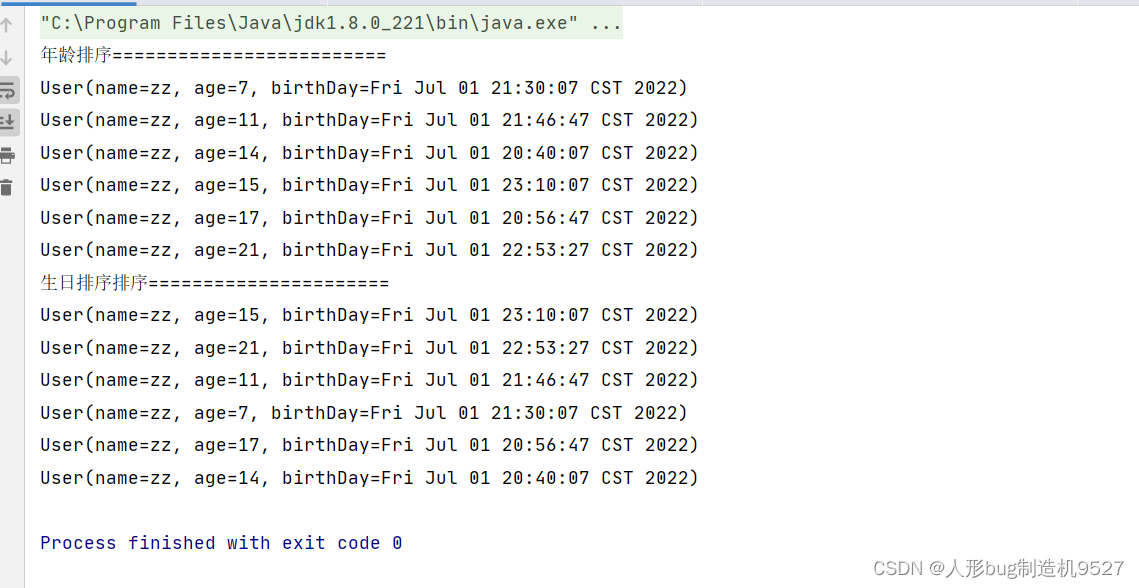
函數式接口,方法引用,Lambda實現的List集合排序小工具

Unity animation day05

Interface fonctionnelle, référence de méthode, Widget de tri de liste implémenté par lambda
随机推荐
Research Report on plastic recycling machine industry - market status analysis and development prospect forecast
Big God explains open source buff gain strategy live broadcast
Interpretation of the champion scheme of CVPR 2020 night target detection challenge
Research Report on market supply and demand and strategy of surgical stapler industry in China
Market trend report, technical innovation and market forecast of tetrabromophthalate (pht4 diol) in China
Can I "reverse" a Boolean value- Can I 'invert' a bool?
Laravel simply realizes Alibaba cloud storage + Baidu AI Cloud image review
MySQL learning notes - data type (2)
[hcie TAC] question 5 - 1
ECCV 2022放榜了:1629篇论文中选,录用率不到20%
How can floating point numbers be compared with 0?
基于check-point实现图数据构建任务
Application of clock wheel in RPC
Scientific research cartoon | what else to do after connecting with the subjects?
Ten clothing stores have nine losses. A little change will make you buy every day
Talking about Net core how to use efcore to inject multiple instances of a context annotation type for connecting to the master-slave database
函數式接口,方法引用,Lambda實現的List集合排序小工具
Digital recognition system based on OpenCV
Research Report on market supply and demand and strategy of China's Sodium Tetraphenylborate (cas+143-66-8) industry
[book club issue 13] packaging format and coding format of audio files