[point cloud processing paper crazy reading classic version 7] - dynamic edge conditioned filters in revolutionary neural networks on Graphs

Abstract

• background ： Many questions can be expressed based on graph Prediction of structural data
• Method ： The convolution operation is extended from mesh to arbitrary graphs, At the same time, frequency domain , Can solve problems of different sizes and connectivity graph
• details ： filters The weight of depends on the edge value from the vertex to the neighborhood ; Developed for graph Deep neural network for classification
• result ： It works well in point cloud classification
• Code ：https://github.com/mys007/ecc (PyTorch edition )

1. introduction

• A graph convolution neural network is constructed in the spatial domain ,filters The weight of depends on the value on the edge , And dynamically update each specific input . The proposed graph convolution network is suitable for any data structure
• The graph convolution network is applied to the point cloud classification task , And achieved better results

2. Related work

Frequency domain method
Spatial domain method

3. Method

3.1 Edge-Conditioned Convolution

Make $l\in \left\{0,..,l_{\max }\right\}$ Index for feedforward neural network layer .

Make $G=$$(V,E)$ Represents an undirected or directed graph , among $V$ Is the vertex. (Vertex) The finite set of $|V|=n$,$E\subseteq V\times V$ Is the edge (Edge) Set $|E|=m$.

Suppose the graph is represented by vertices and edges , namely $X^l:V\mapsto {\mathbb{R}}^{d_l}$ Indicates that each vertex is assigned a value （feature）,$L:E\mapsto {\mathbb{R}}^s$ Indicates that each edge is assigned a value （attribute）. All vertices can be represented in matrix form $X^l\in {\mathbb{R}}^{n\times d_l}$ And all the edges $L\in {\mathbb{R}}^{m\times s},X^0$ Expressed as input signal .

The vertices $i$ Of neighborhood $N(i)=\{j;(j,i)\in E\}\cup \{i\}$ Contains all adjacent vertices and $i$ In itself .

The vertices $i$ Situated filtered The signal $X^l(i)\in {\mathbb{R}}^{d_l}$ Through its neighborhood Point signal $X^{l-1}(j)\in {\mathbb{R}}^{d_{l-1}}$,$j\in N(i)$ The weighted sum of .

Although this way of exchange aggregation solves permutation-invariant and neighborhood The problem of variable size , But this also erases arbitrary structural information .（ It means that the method of aggregation is too violent ？ Updating with only vertices will lose structural information , So the boundary value is introduced as the weight ）

To solve this problem , It is proposed to add filter Condition of weight . Define an input as a boundary value $L(j,i)$ Of filter-generating network $F^l:{\mathbb{R}}^s\mapsto {\mathbb{R}}^{d_l\times d_{l-1}}$, The output is the weight matrix of a specific edge ${\Theta }_{ji}^l\in {\mathbb{R}}^{d_l\times d_{l-1}}$, See the picture 1.

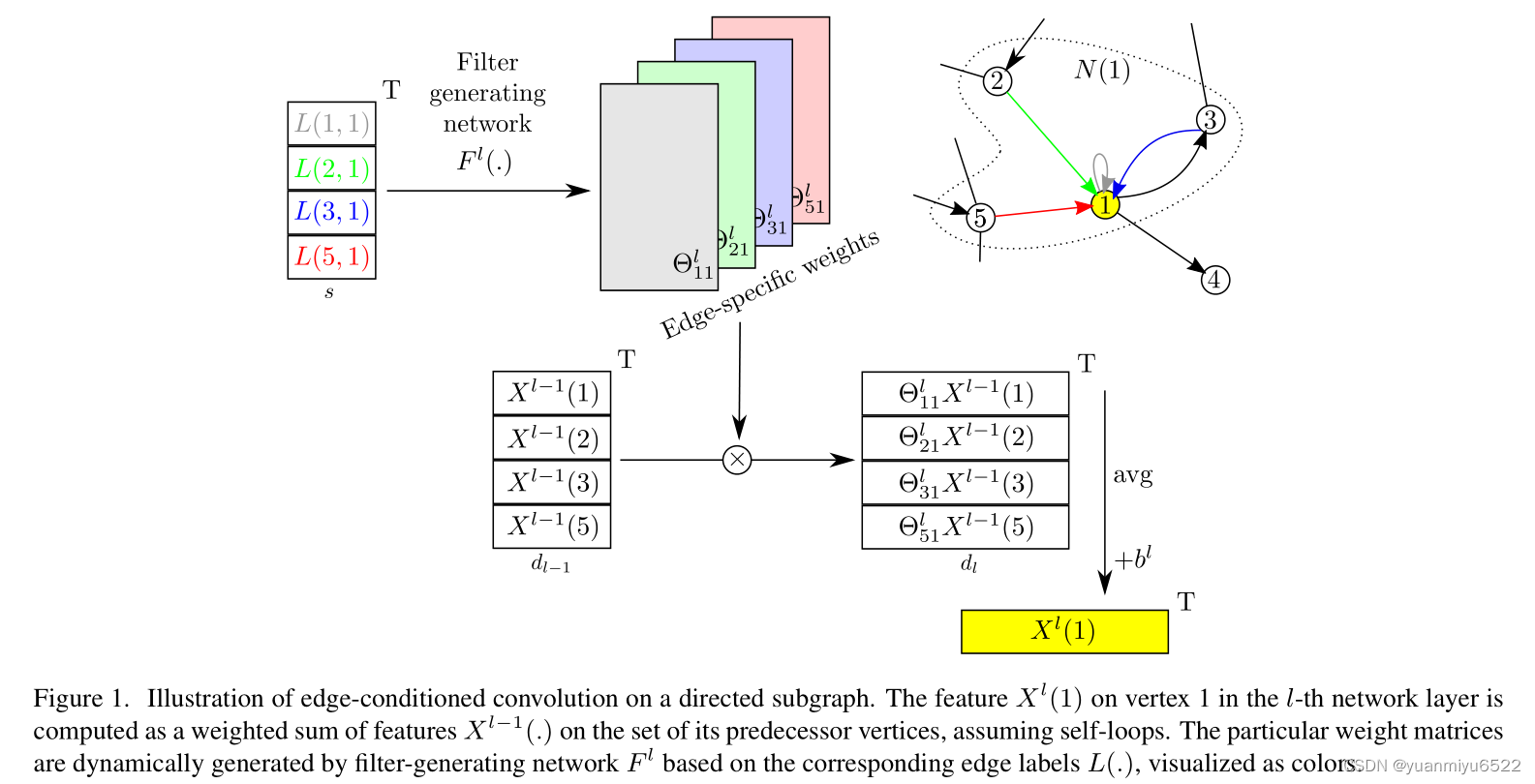
This is called Edge-Conditioned Convolution (ECC) Convolution operation of , It can be expressed as ：
$$\begin{array}{rl}{X}^l(i)& =\frac{1}{|N(i)|}\sum _{j\in N(i)}{F}^l\left(L(j,i);w^l\right)X^{l-1}(j)+b^l\\ & =\frac{1}{|N(i)|}\sum _{j\in N(i)}{\Theta }_{ji}^l{X}^{l-1}(j)+b^l\end{array}$$
among $b^l\in {\mathbb{R}}^{d_l}$ Is a learnable bias ,$F^l$ The learnable parameter of is the network weight $w^l$.$w^l$ and $b^l$ Is the model parameter , Update only during training ,${\Theta }_{ji}^l$ Is based on input graph Parameters generated dynamically by the boundary value of .filter-generating network $F^l$ It can be any derivable model , This paper uses a multi-layer perceptron .

Complexity
Calculate for all vertices $X^l$ At most $m$ Time $F^l$ The evaluation of , as well as $m+n$( Directed graph ) or $2m+n$( Undirected graph ) Submatrix - Vector multiplication . But in GPU It will be more efficient to operate on .

3.2 Relationship to Existing Formulations

Convolution on a regular grid can be seen as ECC A special form of .

3.3. Deep Networks with ECC

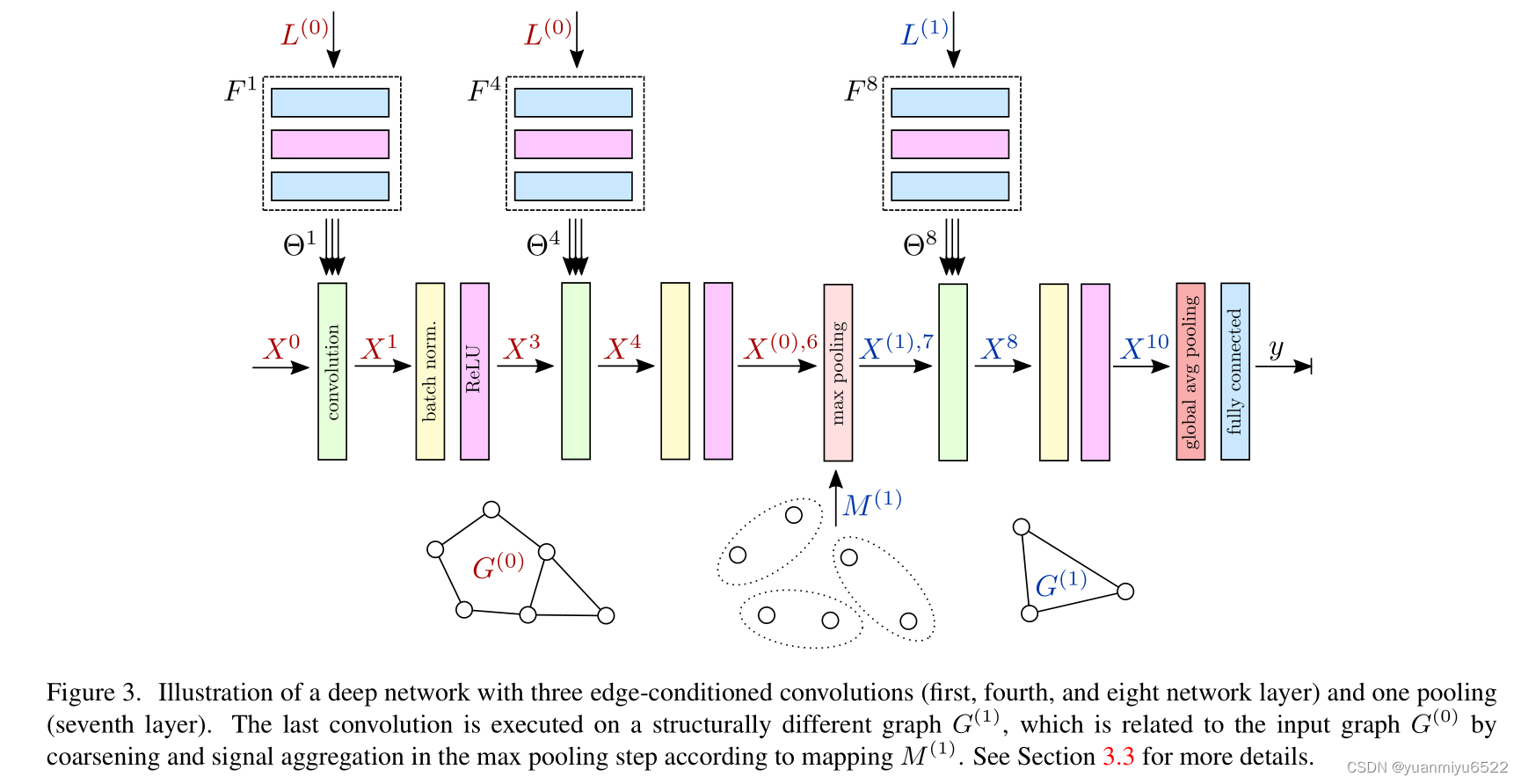
The network structure includes interleaved convolution 、 Global pooling and full connection layer , See the picture 3. In this way , The information obtained from the local neighborhood will be combined layer by layer to get the final context（ Increase the acceptance domain ）. Although the boundary value is specific graph It's fixed , But through filter generating networks the （ Study of the ） explain , It may change from one floor to another （ Not shared between layers $F^l$ The weight of ）. therefore , Only 1-hop neighborhoods The limit ECC Will not be constrained , Similar to the standard CNN Use small 3×3filter In exchange for a deeper network , It's good .

Use after each convolution Batch Normalization, For fast convergence .

Pooling

Even though （non-strided） Convolution layer and all point-wise Layers do not change the foundation graph, And the signal can only be updated on the vertex , But the pooling layer is defined in a new 、coarsened graph Output aggregate signal on the vertex of . therefore , Must be entered for each graph Construct a step by step coarser Of graph $h_{max}$ Of pyramid.

Make $h\in \left\{0,\dots ,h_{\max }\right\}$ Express pyramid Different from graph $G^{(h)}=\left(V^{(h)},E^{(h)}\right)$, every last $G^{(h)}$ Both with $L^{(h)}$ and $X^{(h),l}$ Related to .coarsening The process of includes 3 Step ：

1. subsampling or merging vertices
2. creating the new edge structure $E^{(h)}$ and labeling $L^{(h)}$ (so-called reduction)
3. mapping the vertices in the original graph to those in the coarsened one with $M^{(h)}:V^{(h-1)}\mapsto V^{(h)}$

Final , The index for $l_h$ The pooling layer of will $X^{(h-1),l_{h-1}}$ Aggregate to be based on $M^{(h)}$ Lower dimension of $X^{(h),l_h}$.

stay coarsening In the process of , because self-edge Often appear , Therefore, there will be smaller graph Reduce to several disconnected vertices , There will be no problem . Because this structure is used to deal with variables $n,m$ Of graph, We pass the overall situation average/max Pool operation solves the problem of graph The number of vertices of the change $n^{h_{max}}$.

3.4. Application in Point Clouds

Graph Construction

Given a set of point clouds $P$ And corresponding point features $X_P$, We construct a directed graph $G=(V,E)$, And assign $X^0$ and $L$.

1. For each point $p\in P$ All construct vertices $i\in V$, adopt $X^0(i)=X_P(p)$ Assign the corresponding signal （ If there are no features , Then the assignment is 0）
2. Through the directed edge $(j,i)$ Connect each vertex $i$ And in space neighborhood The summit of $j$ , Experiments show that ,Ball query Better
3. In Cartesian and spherical coordinates ,6D vector $L(j,i)=\left({\delta }_x,{\delta }_y,{\delta }_z,\Vert \delta \Vert ,\arccos {\delta }_z/\Vert \delta \Vert ,\arctan {\delta }_y/{\delta }_x\right)$ As the value on the edge , among $\delta =p_j-p_i$ It means a vertex $j,i$ Offset between .

Graph Coarsening

For a set of input point clouds $P$, adopt VoxelGrid algorithm Get the lower sampling point cloud pyramid $P^{(h)}$, The specific process includes covering the point cloud with a resolution of $r^{(h)}$ The grid of , For each voxel The point in takes the center of mass . Point cloud after each down sampling $P^{(h)}$ Are independently transformed into neighborhood The radius is ${\rho }^{(h)}$ Of graph $G^{(h)}$ and labeling $L^{(h)}$. Definition pooling map $M^{(h)}$, Guarantee $P^{(h-1)}$ Each point in is assigned to the lower sampling point cloud $P^{(h)}$ In the middle distance （$P^{(h-1)}$ Every point in ） Some recent .

Data Augmentation

We randomly rotate point clouds about their upaxis, jitter their scale, perform mirroring, or delete random points.

4. experiment

$\mathrm{C}(c)$ Express ECC The number of output channels is $c$, Follow behind batch normalization and ReLU Activation function .$\mathrm{M}\mathrm{P}(r,\rho )$ Represents the maximum pool layer ,grid A resolution of $r$,neighborhood The radius is $\rho$.$\mathrm{G}\mathrm{A}\mathrm{P}$ Is the average pool layer .$\mathrm{F}\mathrm{C}(c)$ Is the number of channels $c$ The full connection layer of .$\mathrm{D}(p)$ Indicates that the probability is $p$ Of dropouot.

4.1 Sydney Urban Objects

$C(16)-C(32)-MP(0.25,0.5)-C(32)-C(32)-MP(0.75,1.5)-C(64)-MP(1.5,1.5)-GAP-FC(64)-D(0.2)-FC(14)$

$C$ Inside $F^l$ contain $FC(16)-FC(32)-FC(d_l{d}_{l-1})$

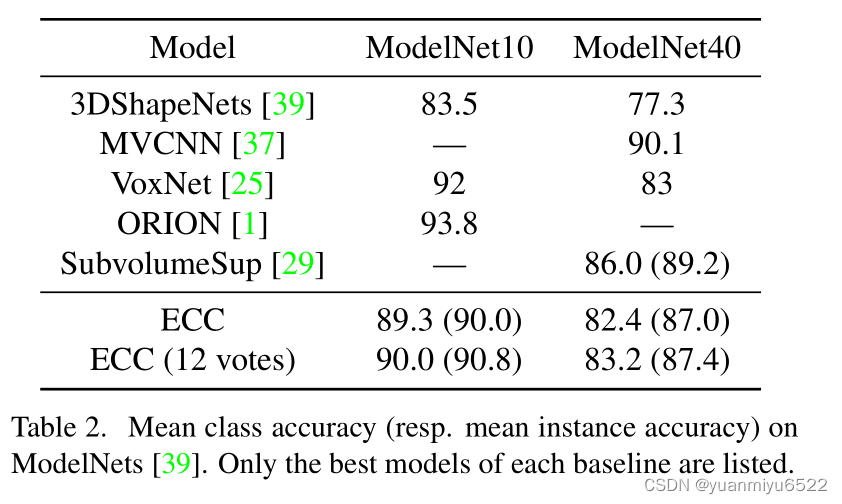
4.2 ModelNet

$C(16)-C(32)-MP(2.5/32,7.5/32)-C(32)-C(32)-MP(7.5/32,22.5/32)-C(64)-GAP-FC(64)-D(0.2)-FC(10)$

$C$ Inside $F^l$ contain $FC(16)-FC(32)-FC(d_l{d}_{l-1})$

New words

• commutative adj. Exchangeable
• interlace v. Interlace , staggered