[graph theory] topological sorting

The concept of topological sorting will not be repeated .

The method of topological sorting

These structures are mainly maintained in the diagram describing topological sorting , The adjacency table is responsible for describing the relationship between points and edges .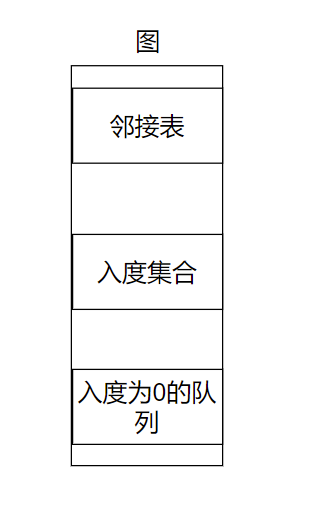

Topological sorting operation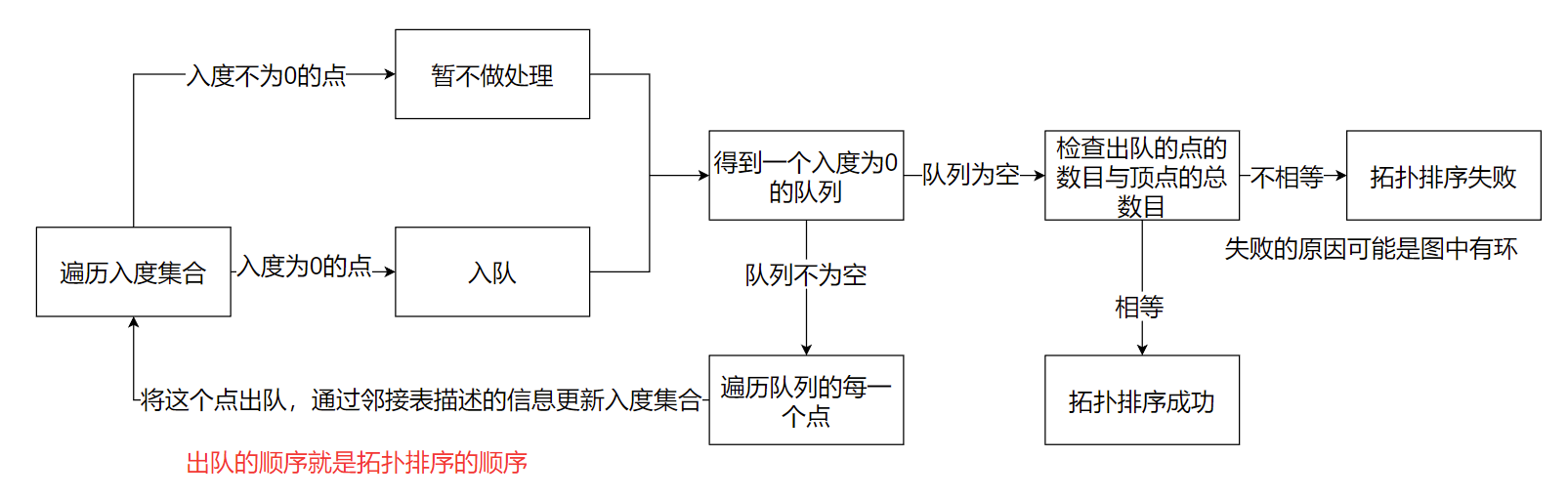

Code implementation

A topological sort （Topological Sorting）_ Shenyi's blog -CSDN Blog _ A topological sort

I followed his introduction to the code

subject

2367 – Genealogical tree (poj.org)
The template questions , Build a graph , Then sort the output .

oj I won't support it C++11, You have to auto Replace with iterators …

#include <iostream>
#include <list>
#include <queue>
#include <vector>
using namespace std;

#define N 1000
queue<int>output;
class Graph
{
public:
	Graph(int v)// Initialize the number of vertices ,new Adjacency list , Initialize the in degree set to 0
		
	{
		_v = v;
		_adj = new list<int>[v];//new One has v Adjacency table of vertices 
		_indegree.resize(v, 0);// Initialize the in degree set 
	}
	~Graph()
	{
		delete[] _adj;
	}
	void addEdge(int val, int w)// The value is val Point of w
	{
		_adj[val].push_back(w);
		_indegree[w]++;
	}
	bool topological_sort()
	{
		for (int i=1;i<_indegree.size();i++)// In fact, there is a layer of mapping at the join node 
		{
			if (!_indegree[i])
			{
				_q.push(i);
			}
		}
		int count = 0;
		while (!_q.empty())
		{
			int v = _q.front();
			_q.pop();
			output.push(v);
			count++;
			// Update the in degree set , Set your entry as 0 The point of joining the team 
			list<int>::iterator it = _adj[v].begin();
			for (;it!=_adj[v].end();it++)
			{
				_indegree[*it]--;
				if (!_indegree[*it])
				{
					_q.push(*it);
				}
			}
		}
		if (count<_v)// Graph with loop 
		{
			return false;
		}
		else
		{
			return true;
		}
	}
private:
	int _v;// Number of vertices 
	list<int>* _adj;// Adjacency list 
	queue<int>_q;// The maintenance degree is 0 The set of vertices of 
	vector<int> _indegree;// Record the depth of each vertex 
};


int main()
{
	int n;
	cin >> n;
	Graph g(n+1);
	for (int i = 1; i <= n; i++)
	{
		int x;
		while (cin >> x)
		{
			if (x == 0)
			{
				break;
			}
			g.addEdge(i, x);
		}
	}
	g.topological_sort();
	bool flag = 1;
	while (!output.empty())
	{
		int x = output.front();
		output.pop();
		if (flag)
		{
			cout << x;
			flag = 0;
		}
		else
		{
			cout << " " << x;
		}
	}
	return 0;
}