当前位置:网站首页>【力扣刷题】一维动态规划记录(53零钱兑换、300最长递增子序列、53最大子数组和)
【力扣刷题】一维动态规划记录(53零钱兑换、300最长递增子序列、53最大子数组和)
2022-07-06 12:56:00 【李小恩恩子】
目录
一、322.零钱兑换
题目
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。

解题思路
首先先明确dp数组的定义:输入一个目标金额n,返回凑出目标金额的最少硬币数量。
【base case】:amount = 0,返回0;
【状态】:唯一的目标金额;
【选择】:每选择了一枚硬币,就相当于减少了目标金额。
【状态转移方程】:
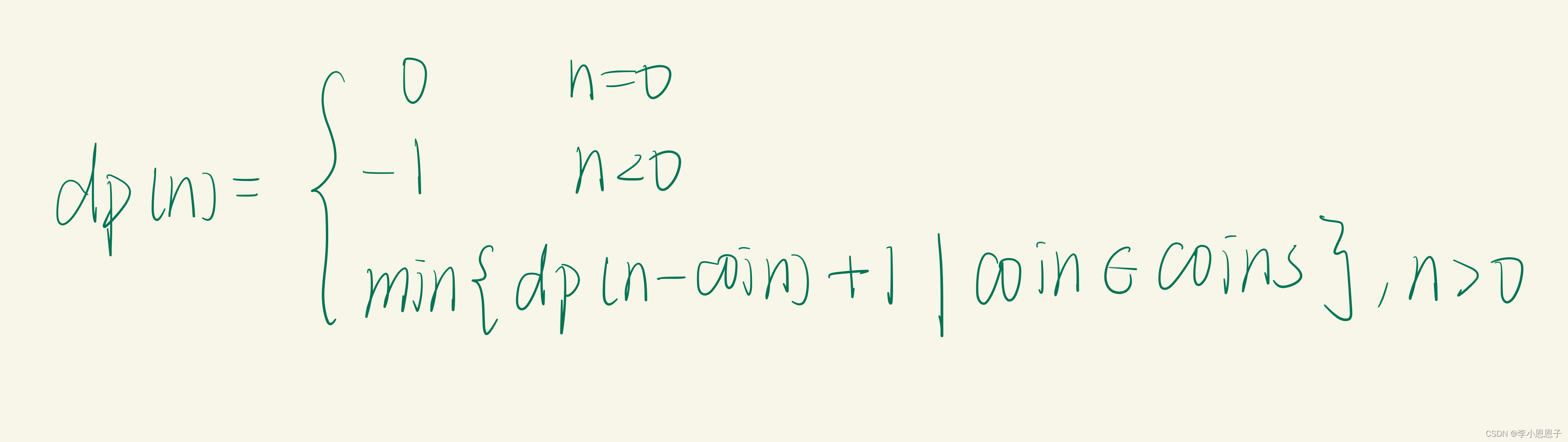
代码
自顶向下:带记忆的向下搜索,减少求解子问题的数量
class Solution {
public int coinChange(int[] coins, int amount) {
//一维
//记忆化搜索
//dp数组表示输入目标金额amount返回凑出目标金额最小的硬币数量
int[] dp = new int[amount + 1];
for(int i = 0;i <= amount;i++){
dp[i] = -99;//随便初始化一个特殊值,用来判断
}
return coin(coins,dp,amount);
}
public int coin(int[] coins,int[] dp,int amount){
if(amount == 0) return 0;
if(amount < 0) return -1;
//不重复计算,剪枝
if(dp[amount] != -99) return dp[amount];
int res = Integer.MAX_VALUE;
for(int coin = 0; coin < coins.length;coin++){
//子问题
int next = coin(coins,dp,amount-coins[coin]);
//子问题无解
if(next == -1) continue;
//在所有子问题中选出最优解,+1
res = Math.min(res,next + 1);
}
//记录结果,减少重复计算
dp[amount] = (res == Integer.MAX_VALUE) ? -1:res;
return dp[amount];
}
}自底向上:dp数组的迭代求解
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
//amount+1相当于无穷大了,因为硬币数量最大也就是amount(全为1块的硬币的情况)
for(int i = 0;i < amount + 1 ; i++){
dp[i] = amount + 1;
}
dp[0] = 0;
for(int i = 0; i < amount + 1;i++){
//求所有子问题的最优解+1
for(int coin = 0; coin < coins.length; coin++){
if(i - coins[coin] < 0) continue;
dp[i] = Math.min(dp[i],dp[i - coins[coin]] + 1);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
}二、300.最长递增子序列
题目
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

解题思路
注意是要求子序列,不是子数组,子数组是连续的,子序列不是,可以不用连续。如上面示例1的子序列【2,3,7,101】。
dp数组的定义:dp[i]表示以nums[i]这个数结尾的最长递增子序列。
【base case】:dp[i]所有的值初始化为1,因为以nums[i]结尾的最长递增子序列最起码包括自己
【选择】:对于每一个dp[i],只需要找到前面所有比它小的元素的dp[j],再+1,找到其中的最大值即dp[i]。
【结果】:子序列的最大值,是dp数组中的最大值。
代码
class Solution {
public int lengthOfLIS(int[] nums) {
//动态规划
//定义dp[i]表示以元素nums[i]结尾的最长递增子序列
//对于每一个dp[i],只需要找到前面所有比它小的元素的dp[j],再+1,找到其中的最大值即dp[i]
int[] dp = new int[nums.length];
for(int i = 0; i < nums.length;i++){
dp[i] = 1;//初始化,所有元素为1
}
int res = 1;
for(int i = 0; i < nums.length;i++){
for(int j = 0; j < i; j++){
if(nums[j] < nums[i]){
dp[i] = Math.max(dp[i],dp[j] + 1);
}
}
res = Math.max(res,dp[i]);
}
return res;
}
}三、53.最大子数组和
题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。

解题思路
和上面求【最长递增子序列】类似,定义dp数组含义:dp[i]表示以nums[i]结尾的最大子数组和。
【注意】:如果定义dp[i]数组为nums[0...i]中的最大子数组和,那么是求不出来的,因为推不出来dp[i+1],子数组必须是连续的,但不能保证dp[i]到dp[i+1]的时候:nums[0...i]中的最大子数组与nums[i+1]是相邻的。
【base case】:dp[0] = nums[0]
【选择】:判断大小做选择,①和前面相邻的元素连接组成更大子数组;②自己作为一个子数组
【结果】:子数组最大和,是dp数组中的最大值。
代码
class Solution {
public int maxSubArray(int[] nums) {
//动态规划
//定义dp[i]表示以nums[i]结尾的最大子数组和
//动态转移有两种选择,第一种和前面一个元素组合成更大的和,第二种自己一个人组
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i = 1;i < nums.length;i++){
dp[i] = Math.max(nums[i],dp[i - 1] + nums[i]);
}
int res = Integer.MIN_VALUE;
for(int i = 0 ; i < nums.length;i++){
res = Math.max(res,dp[i]);
}
return res;
}
}其实我看到这个题目首先想的也是滑动窗口,因为滑动窗口最适合解决求连续的子串、子数组等问题,但是这个数组元素里面有负数,用滑动窗口是做不出来的,因为改变窗口左右指针的条件不明确。
题目二、题目三属于同一类动态规划问题。
边栏推荐
- el-table表格——sortable排序 & 出现小数、%时排序错乱
- Nodejs教程之让我们用 typescript 创建你的第一个 expressjs 应用程序
- The biggest pain point of traffic management - the resource utilization rate cannot go up
- What is the problem with the SQL group by statement
- Aike AI frontier promotion (7.6)
- 2017 8th Blue Bridge Cup group a provincial tournament
- SAP UI5 框架的 manifest.json
- Simple continuous viewing PTA
- C # use Oracle stored procedure to obtain result set instance
- PG基础篇--逻辑结构管理(事务)
猜你喜欢
Comprehensive evaluation and recommendation of the most comprehensive knowledge base management tools in the whole network: flowus, baklib, jiandaoyun, ones wiki, pingcode, seed, mebox, Yifang cloud,
![[200 opencv routines] 220 Mosaic the image](/img/75/0293e10ad6de7ed86df4cacbd79b54.png)
[200 opencv routines] 220 Mosaic the image
Pycharm remote execution
Swagger UI教程 API 文档神器

MLP (multilayer perceptron neural network) is a multilayer fully connected neural network model.

防火墙基础之外网服务器区部署和双机热备

Is it profitable to host an Olympic Games?

Hardware development notes (10): basic process of hardware development, making a USB to RS232 module (9): create ch340g/max232 package library sop-16 and associate principle primitive devices
![[asp.net core] set the format of Web API response data -- formatfilter feature](/img/6b/e3d513f63b244f9f32555d3b3bec8c.jpg)
[asp.net core] set the format of Web API response data -- formatfilter feature

硬件开发笔记(十): 硬件开发基本流程,制作一个USB转RS232的模块(九):创建CH340G/MAX232封装库sop-16并关联原理图元器件
随机推荐
Is it safe to open an account in flush? Which securities company is good at opening an account? Low handling charges
1500萬員工輕松管理,雲原生數據庫GaussDB讓HR辦公更高效
ACdreamoj1110(多重背包)
Hardware development notes (10): basic process of hardware development, making a USB to RS232 module (9): create ch340g/max232 package library sop-16 and associate principle primitive devices
Pat 1078 hashing (25 points) ⼆ times ⽅ exploration method
7. Data permission annotation
Introduction to the use of SAP Fiori application index tool and SAP Fiori tools
Comprehensive evaluation and recommendation of the most comprehensive knowledge base management tools in the whole network: flowus, baklib, jiandaoyun, ones wiki, pingcode, seed, mebox, Yifang cloud,
HMS core machine learning service creates a new "sound" state of simultaneous interpreting translation, and AI makes international exchanges smoother
Seven original sins of embedded development
OneNote 深度评测:使用资源、插件、模版
快过年了,心也懒了
Web开发小妙招:巧用ThreadLocal规避层层传值
This year, Jianzhi Tencent
@GetMapping、@PostMapping 和 @RequestMapping详细区别附实战代码(全)
[redis design and implementation] part I: summary of redis data structure and objects
Chris LATTNER, the father of llvm: why should we rebuild AI infrastructure software
C # use Oracle stored procedure to obtain result set instance
c#使用oracle存储过程获取结果集实例
El table table - sortable sorting & disordered sorting when decimal and% appear