当前位置:网站首页>[point cloud processing paper crazy reading classic version 14] - dynamic graph CNN for learning on point clouds
[point cloud processing paper crazy reading classic version 14] - dynamic graph CNN for learning on point clouds
2022-07-03 09:08:00 【LingbinBu】
DGCNN:Dynamic Graph CNN for Learning on Point Clouds
Abstract
- background : For many applications in computer graphics ,point clouds It is a flexible geometric representation , Usually most 3D Raw output of the acquisition device
- problem : Even though point clouds Of hand-designed Features have been proposed a long time ago , But recently in image It's very hot convolutional neural networks(CNNs) Indicates that CNN Applied to the point clouds The value of .Point clouds Lack of topology information , So we need to design a model that can recover topology information , So as to enrich point clouds Express the purpose of ability
- Method : stay CNN There is an embedded one called EdgeConv Module
- EdgeConv The module functions in graphs On , Dynamically evaluate each layer of the network graphs Calculate
- EdgeConv Modules can be exported , And can be embedded in any existing network
- EdgeConv The module considers local neighborhood information and global shape information
- EdgeConv It has sort invariance
- In feature space multi-layer systems affinity Collect the potential long-distance semantic features in the original embedding .
- Code :

Method
- In order to mine local geometry , Construct a local neighborhood graph, And apply convolution operation on the edge , Edges connect adjacent pairs of points .
- Article graph Unfixed , Dynamically update at every layer of the network , in other words , One point k N N kNN kNN The elements in the set change from layer to layer in the network , It's through embeddings Sequence calculation .
- Proximity and input in feature space are different , This will lead to the nonlocal diffusion of information in the whole point cloud .
Edge Convolution
remember X = { x 1 , … , x n } ⊆ R F \mathbf{X}=\left\{\mathbf{x}_{1}, \ldots, \mathbf{x}_{n}\right\} \subseteq \mathbb{R}^{F} X={ x1,…,xn}⊆RF Enter a point cloud for , among n n n Is the number of points , F F F It's the dimension of a point , In the simplest case , F = 3 F=3 F=3, Every point includes 3D coordinate x i = ( x i , y i , z i ) \mathbf{x}_{i}=\left(x_{i}, y_{i}, z_{i}\right) xi=(xi,yi,zi), In other cases , Colors will also be included 、 Normal vector, etc , At other layers of the network , F F F Represents the characteristic dimension of the point .
We calculate a directed graph G = ( V , E ) \mathcal{G}=(\mathcal{V}, \mathcal{E}) G=(V,E) , Represents the local point cloud structure , among V = { 1 , … , n } \mathcal{V}=\{1, \ldots, n\} V={ 1,…,n}, E ⊆ V × V \mathcal{E} \subseteq \mathcal{V} \times \mathcal{V} E⊆V×V They are vertices and edges . In the simplest case , Construct a X \mathrm{X} X Of KNN graph G \mathcal{G} G. The graph Include self-loop, Each node points to itself . Define the edge feature as e i j = h Θ ( x i , x j ) \boldsymbol{e}_{i j}=h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) eij=hΘ(xi,xj), among h Θ : R F × h_{\Theta}: \mathbb{R}^{F} \times hΘ:RF× R F → R F ′ \mathbb{R}^{F} \rightarrow \mathbb{R}^{F^{\prime}} RF→RF′ It's a nonlinear function , The learnable parameters are Θ \boldsymbol{\Theta} Θ.
Last , By using channel Symmetric aggregation operation in units □ \square □ (e.g., ∑ \sum ∑ or max) Definition EdgeConv operation , Aggregate on edge features associated with all edges emitted from each vertex . In the i i i Vertex EdgeConv The output is expressed as :
x i ′ = □ j : ( i , j ) ∈ E h Θ ( x i , x j ) \mathbf{x}_{i}^{\prime}=\mathop {\square}\limits_{ {j:(i, j) \in \mathcal{E}}} h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) xi′=j:(i,j)∈E□hΘ(xi,xj)
among x i \mathbf{x}_{i} xi yes central point, { x j : ( i , j ) ∈ E } \left\{\mathbf{x}_{j}:(i, j) \in \mathcal{E}\right\} { xj:(i,j)∈E} yes x i \mathbf{x}_{i} xi Of neigboured points. To make a long story short , Given with n n n Point F F F Dimensional point cloud ,EdgeConv Will produce an equal number of points F ′ F^{\prime} F′ Dimensional point cloud .

Choice of h h h and □ \square □
h h h The choice of :
- Convolution :
x i m ′ = ∑ j : ( i , j ) ∈ E θ m ⋅ x j . x_{i m}^{\prime}=\sum_{j:(i, j) \in \mathcal{E}} \boldsymbol{\theta}_{m} \cdot \mathbf{x}_{j} . xim′=j:(i,j)∈E∑θm⋅xj.
among Θ = ( θ 1 , … , θ M ) \Theta=\left(\theta_{1}, \ldots, \theta_{M}\right) Θ=(θ1,…,θM) Yes M M M Different filters Weight coding . Every θ m \theta_{m} θm All have a relationship with x \mathbf{x} x The same dimension , ⋅ \cdot ⋅ Represent inner product . - PointNet type :
h Θ ( x i , x j ) = h Θ ( x i ) , h_{\Theta}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=h_{\Theta}\left(\mathbf{x}_{i}\right), hΘ(xi,xj)=hΘ(xi),
Only encode global shape information , Without considering the local neighborhood structure , Count as EdgeConv A special case of . - Atzmon Proposed PCNN type :
x i m ′ = ∑ j ∈ V ( h θ ( x j ) ) g ( u ( x i , x j ) ) , x_{i m}^{\prime}=\sum_{j \in \mathcal{V}}\left(h_{\boldsymbol{\theta}\left(\mathbf{x}_{j}\right)}\right) g\left(u\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\right), xim′=j∈V∑(hθ(xj))g(u(xi,xj)),
among g g g It's Gauss kernel, u u u It is used to calculate the distance in European space . - PointNet++ type :
h Θ ( x i , x j ) = h Θ ( x j − x i ) . h_{\boldsymbol{\Theta}}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=h_{\boldsymbol{\Theta}}\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right) . hΘ(xi,xj)=hΘ(xj−xi).
Encode only local information , Divide the whole shape into many blocks , Lost global structure information . - The symmetric edge function used in this paper :
h Θ ( x i , x j ) = h ˉ Θ ( x i , x j − x i ) . h_{\boldsymbol{\Theta}}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\bar{h}_{\boldsymbol{\Theta}}\left(\mathbf{x}_{i}, \mathbf{x}_{j}-\mathbf{x}_{i}\right) . hΘ(xi,xj)=hˉΘ(xi,xj−xi).
It combines the global shape structure ( By way of x i \mathbf{x}_{i} xi Is determined by the coordinates of the center ), Local neighborhood information is also considered ( adopt x j − x i \mathbf{x}_{j}-\mathbf{x}_{i} xj−xi obtain ).
Specially , It can also be expressed by the following formula EdgeConv The operation of :
e i j m ′ = ReLU ( θ m ⋅ ( x j − x i ) + ϕ m ⋅ x i ) , e_{i j m}^{\prime}=\operatorname{ReLU}\left(\boldsymbol{\theta}_{m} \cdot\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)+\boldsymbol{\phi}_{m} \cdot \mathbf{x}_{i}\right), eijm′=ReLU(θm⋅(xj−xi)+ϕm⋅xi),
And then execute :
x i m ′ = max j : ( i , j ) ∈ E e i j m ′ , x_{i m}^{\prime}=\max _{j:(i, j) \in \mathcal{E}} e_{i j m}^{\prime}, xim′=j:(i,j)∈Emaxeijm′,
among Θ = ( θ 1 , … , θ M , ϕ 1 , … , ϕ M ) \Theta=\left(\theta_{1}, \ldots, \theta_{M}, \phi_{1}, \ldots, \phi_{M}\right) Θ=(θ1,…,θM,ϕ1,…,ϕM).
□ \square □ Choose as max
Dynamic Graph Update
Our experiments show that , Use the nearest neighbor in the feature space generated by each layer to recalculate graph It is useful to . This is our method with fixed input graph Working on graph CNN A key difference . This dynamic graph Update is the name of our architecture DGCNN Why .
In each layer , It's different graph G ( l ) = ( V ( l ) , E ( l ) ) \mathcal{G}^{(l)}=\left(\mathcal{V}^{(l)}, \mathcal{E}^{(l)}\right) G(l)=(V(l),E(l)), Among them the first l l l The form of the edge of the layer is ( i , j i 1 ) , … , ( i , j i k l ) \left(i, j_{i 1}\right), \ldots,\left(i, j_{i k_{l}}\right) (i,ji1),…,(i,jikl), That is to say x j i 1 ( l ) , … , x j i k l ( l ) \mathbf{x}_{j_{i 1}}^{(l)}, \ldots, x_{j_{i k_{l}}}^{(l)} xji1(l),…,xjikl(l) It's distance x i ( l ) \mathbf{x}_{i}^{(l)} xi(l) Current k l k_{l} kl A little bit . Our network learns how to construct graph G \mathcal{G} G, It is not fixed before the network starts to predict . At the time of implementation , Calculate the distance matrix in the distance space , Then take the nearest for each single point k k k A little bit .
Properties
Permutation Invariance
Consider that the output of each layer is :
x i ′ = max j : ( i , j ) ∈ E h Θ ( x i , x j ) , \mathbf{x}_{i}^{\prime}=\max _{j:(i, j) \in \mathcal{E}} h_{\boldsymbol{\Theta}}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right), xi′=j:(i,j)∈EmaxhΘ(xi,xj),
because max Is a symmetric function , So the output layer x i ′ \mathrm{x}_{i}^{\prime} xi′ Relative to input x j \mathbf{x}_{j} xj It's sort invariant . The global maximum pool operation is also sort invariant for the characteristics of aggregation points .
Translation Invariance
Our operation has a part translation invariance nature , Because the edge function formula is not affected by translation , It can also be selectively affected translation influence . Consider at point x j \mathbf{x}_{j} xj Sum point x i \mathbf{x}_{i} xi Pan on , When translation T T T when , Yes :
e i j m ′ = θ m ⋅ ( x j + T − ( x i + T ) ) + ϕ m ⋅ ( x i + T ) = θ m ⋅ ( x j − x i ) + ϕ m ⋅ ( x i + T ) \begin{aligned} e_{i j m}^{\prime} &=\boldsymbol{\theta}_{m} \cdot\left(\mathbf{x}_{j}+T-\left(\mathbf{x}_{i}+T\right)\right)+\boldsymbol{\phi}_{m} \cdot\left(\mathbf{x}_{i}+T\right) \\ &=\boldsymbol{\theta}_{m} \cdot\left(\mathbf{x}_{j}-\mathbf{x}_{i}\right)+\boldsymbol{\phi}_{m} \cdot\left(\mathbf{x}_{i}+T\right) \end{aligned} eijm′=θm⋅(xj+T−(xi+T))+ϕm⋅(xi+T)=θm⋅(xj−xi)+ϕm⋅(xi+T)
If you make ϕ m = 0 \boldsymbol{\phi}_{m}=\mathbf{0} ϕm=0 when , Only consider x j − x i \mathbf{x}_{j}-\mathbf{x}_{i} xj−xi, Then the operation is completely translational . But the model will lose the acquisition of local information , So it's still part translation invariance.
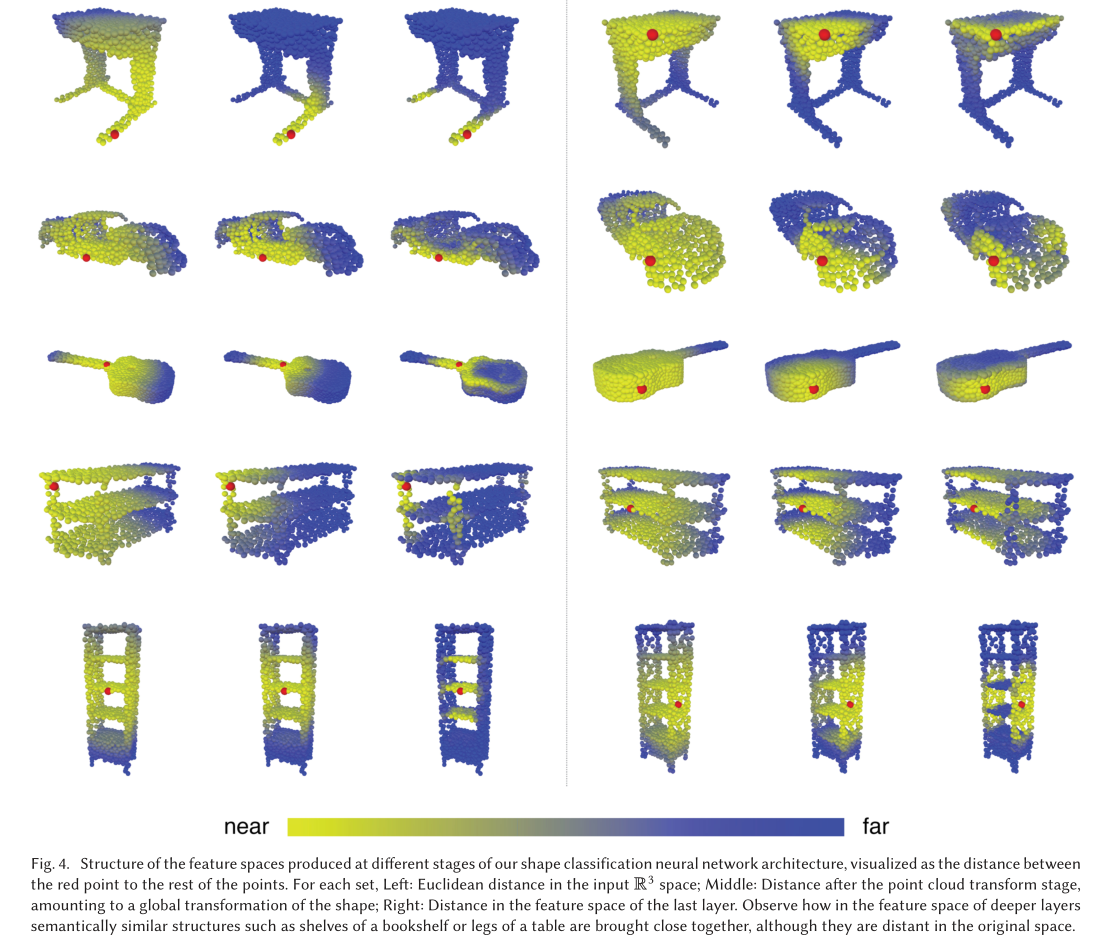

experiment
Classification

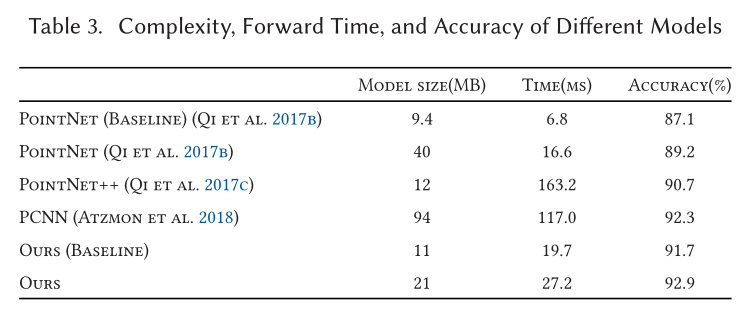
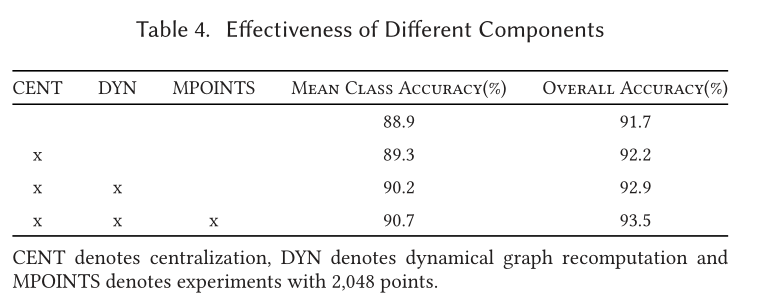
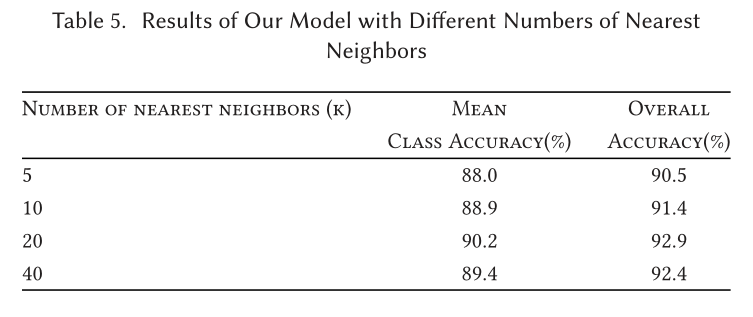
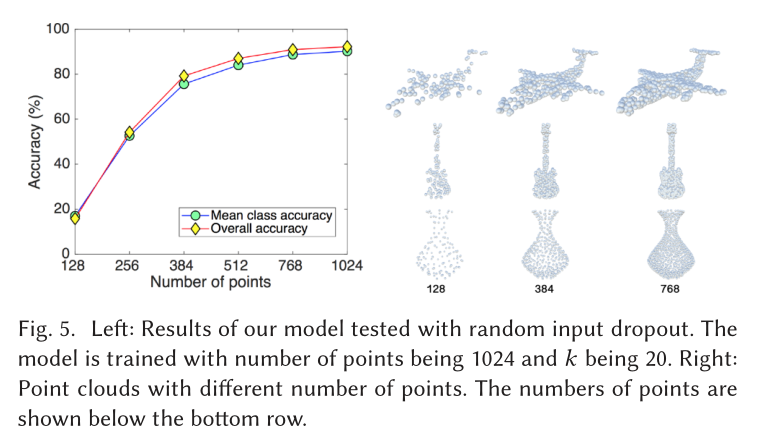
Part Segmentation


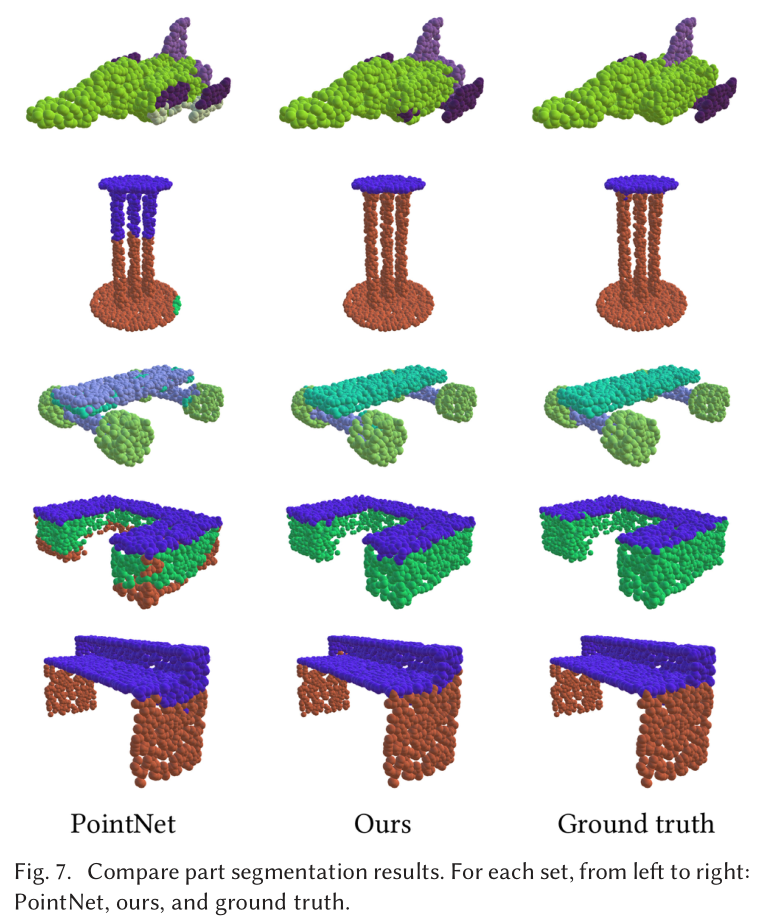
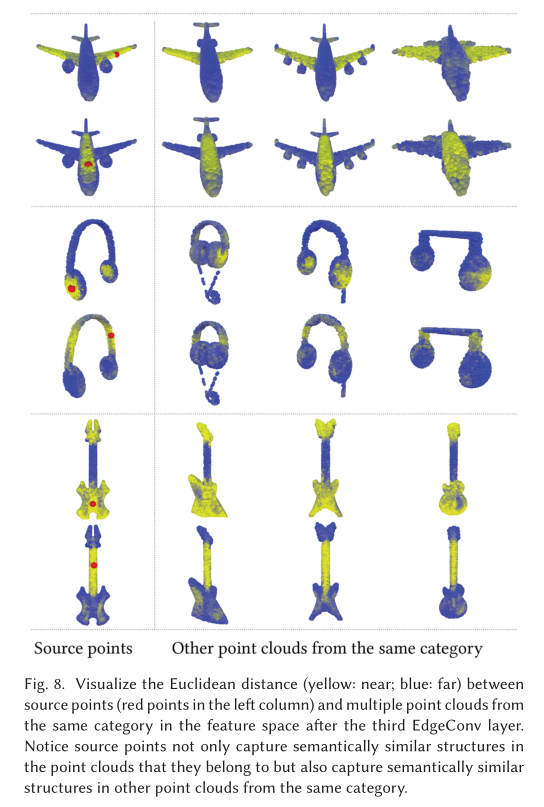

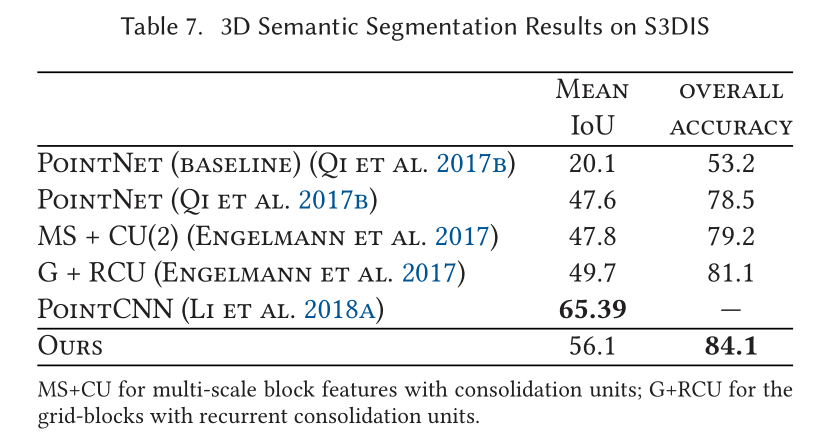
Indoor Scene Segmentation

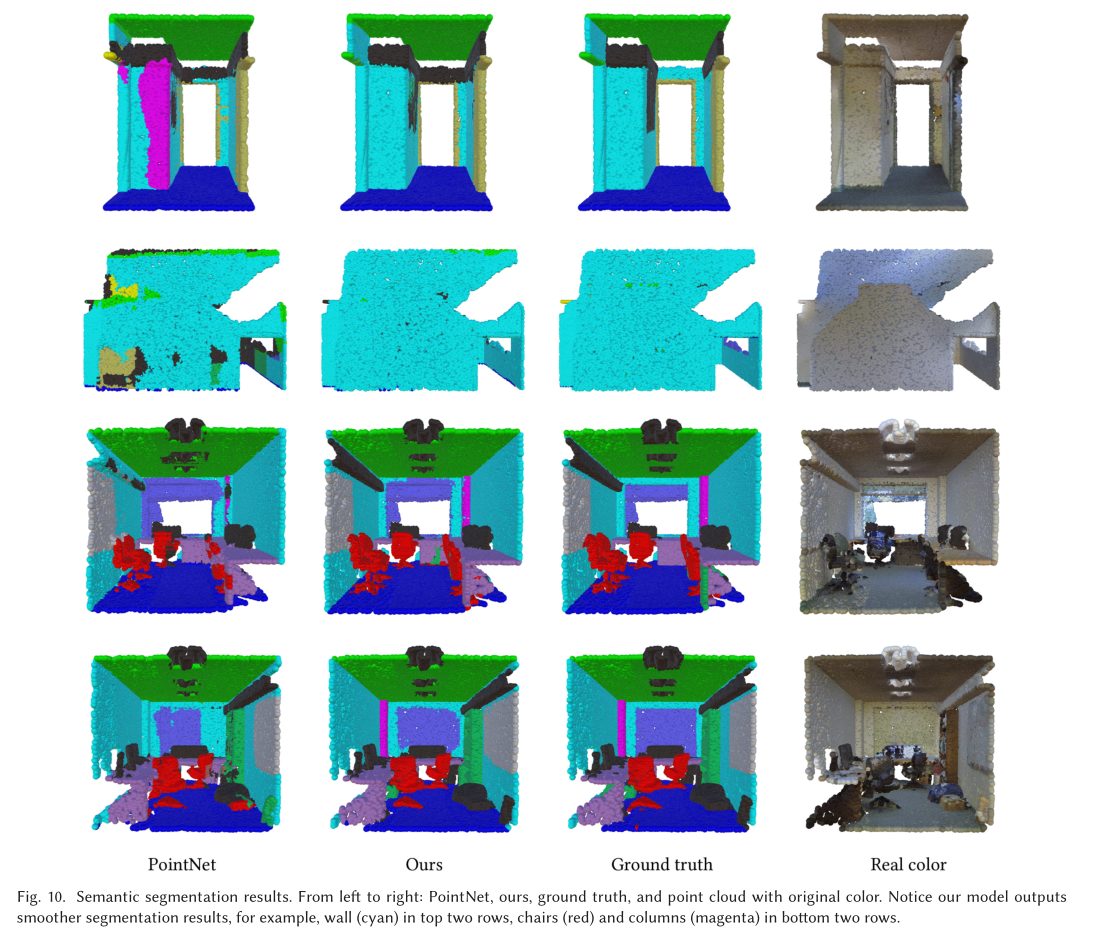
expectation
- Improve the speed of the model by combining faster data formats , Use multivariate groups instead , Don't look for the relationship between point pairs
- Design a non shared transformer The Internet , At every local patch They are all different , More flexibility
New words
- dub v go by the name of …
- arguably adv Can be said to be
- emanate v issue
边栏推荐
- AcWing 785. 快速排序(模板)
- 数位统计DP AcWing 338. 计数问题
- The method of replacing the newline character '\n' of a file with a space in the shell
- Introduction to the usage of getopts in shell
- On the setting of global variable position in C language
- Methods of using arrays as function parameters in shell
- 状态压缩DP AcWing 291. 蒙德里安的梦想
- Save the drama shortage, programmers' favorite high-score American drama TOP10
- LeetCode 1089. 复写零
- CSDN markdown editor help document
猜你喜欢

How to place the parameters of the controller in the view after encountering the input textarea tag in the TP framework

Instant messaging IM is the countercurrent of the progress of the times? See what jnpf says

LeetCode 241. 为运算表达式设计优先级

AcWing 785. 快速排序(模板)
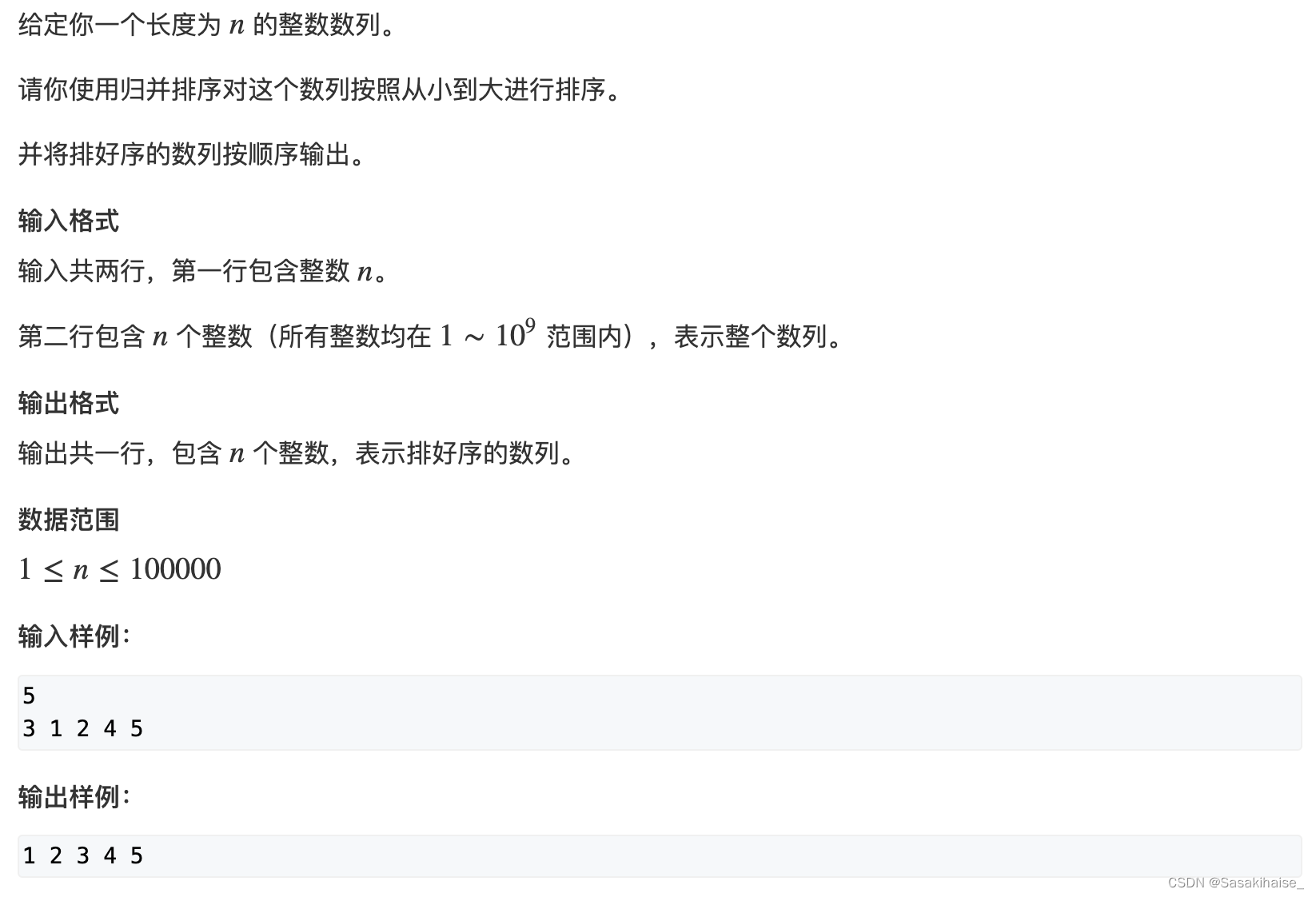
AcWing 787. Merge sort (template)
Debug debugging - Visual Studio 2022
传统企业数字化转型需要经过哪几个阶段?

excel一小时不如JNPF表单3分钟,这样做报表,领导都得点赞!

Query XML documents with XPath

20220630 learning clock in
随机推荐
数位统计DP AcWing 338. 计数问题
LeetCode 1089. 复写零
dried food! What problems will the intelligent management of retail industry encounter? It is enough to understand this article
Save the drama shortage, programmers' favorite high-score American drama TOP10
求组合数 AcWing 886. 求组合数 II
On a un nom en commun, maître XX.
LeetCode 532. K-diff number pairs in array
【点云处理之论文狂读经典版11】—— Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling
低代码起势,这款信息管理系统开发神器,你值得拥有!
Common DOS commands
Notes and bugs generated during the use of h:i:s and y-m-d
【点云处理之论文狂读前沿版10】—— MVTN: Multi-View Transformation Network for 3D Shape Recognition
DOM render mount patch responsive system
LeetCode 438. Find all letter ectopic words in the string
Really explain the five data structures of redis
CSDN markdown editor help document
Method of intercepting string in shell
Sword finger offer II 029 Sorted circular linked list
Tag paste operator (#)
LeetCode 57. Insert interval