当前位置:网站首页>【Games101】Transformation
【Games101】Transformation
2022-06-30 00:47:00 【Missnish】
- Linear algebra related
- Vector point multiplication → Obtain direction
- Vector cross product → Get around & domestic and foreign
- linear transformation : A transformation that keeps the mesh parallel and equidistant
The properties of linear transformation :
- All the lines are still straight ( Including diagonals )
- The origin is still the origin , No movement
- How do we understand Transformation( Transformation )?
ordinary , We can understand it as a series of steps , Through these steps , It can realize the transformation from three-dimensional space to two-dimensional image .

One 、 A two-dimensional / Three dimensional transformation
The zoom (Scale)

symmetry (Reflection)

shear (Shear)

rotate (Rotation)

Affine transformation = linear transformation + Translation transformation

Homogeneous coordinates :
because 2D The transform has no offset , So it's impossible to say 2D Pan operation , The main function of homogeneous coordinates is to introduce offset , Translate transform (Translate) Unified classification 2D Transformation , You don't want the translation transform to be different from the others 2D Transformation .
At the same time, homogeneous coordinates can distinguish points from vectors , According to the translation invariance of the vector , Vectorial w Shaft for 0, Dot w Shaft for 1.

With homogeneous coordinates , The translation transformation is expressed as follows :

Combination transformation
(1) Properties based on rotation calculation ( Rotate around the origin ), When multiple transformation matrices are calculated, they are usually rotated first and then translated .
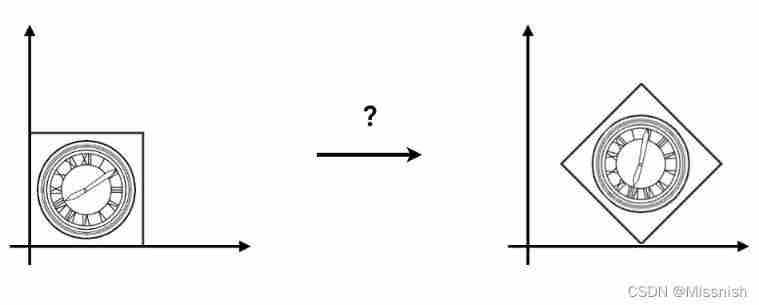

(2) For an image that is not at the origin , How to perform rotation transformation ?
First, translate the image to the origin , The original position will be translated after the transformation operation .

Summary of basic transformation matrix

Two 、MVP Transformation
MVP The transformation consists of three transformations , namely Model Transformation、View / Camera Transformation、Projection Transformation.

Model transformation (placing objects)
The objects in the world coordinate system , Using a change matrix, their vertex coordinates are transformed from local to local Local Coordinate system ( relative ) Switch to the world Global Coordinate system ( absolute ), the DCC Model coordinates in are converted to model coordinates in the engine .
View transformation (placing camera)
Put the world coordinate system ( The center of the world is the origin ) To the camera coordinate system ( Camera position is the origin ), Realize the transformation from the third perspective to the first perspective .
(1) How do we define a camera ?
We define the position of the camera as  , Orientation is defined as
, Orientation is defined as  , Up ( It's like an antenna ) Defined as
, Up ( It's like an antenna ) Defined as  .
.

(2) How to achieve M→V Transformation ?
Pan the camera to the origin , 、
、 、
、 Rotate to
Rotate to  、
、 、
、 .
.
among , /
/ It's the camera up ( The antenna ),
It's the camera up ( The antenna ), /
/ Is the viewing direction of the camera , Cross multiply to get
Is the viewing direction of the camera , Cross multiply to get  /
/ .
.
thus  、
、 、
、 The model space coordinate system is converted to
The model space coordinate system is converted to  、
、 、
、 Observation space coordinate system .
Observation space coordinate system .

(3) How to calculate the target rotation matrix ?
Rotation matrix solution : First find the rotation matrix from the origin to the camera , Then inverse the rotation matrix from the camera to the origin .


notes : The inverse of the rotation matrix = Transpose matrix of rotation matrix
Projection transformation
The space observed by the camera is usually a visual cone , The projection transformation transforms the viewing cone into a 1×1×1 Standard Cube , To facilitate subsequent operations .
There are two forms of projection transformation , Perspective projection (Perspective Projection) And orthogonal projection (Orthographic Projection).
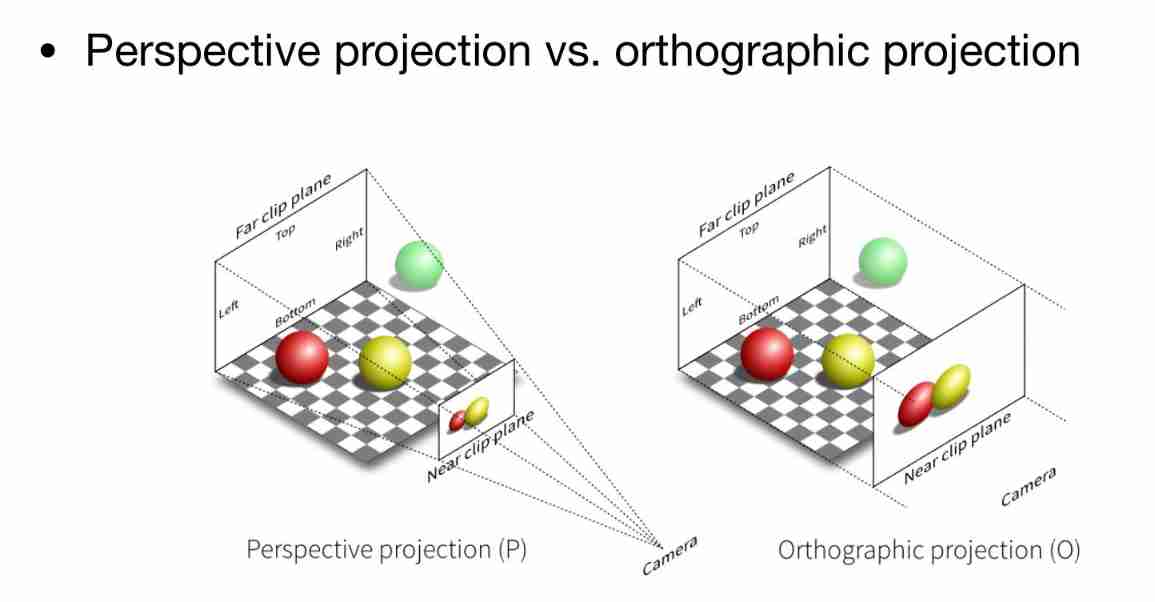
(1) Orthographic projection (Orthographic Projection)
How to understand orthogonal projection ?

We set the space of all objects as a cube , Translate and zoom the cube , It becomes a point centered on the origin 1×1×1 Standard Cube .

The transformation matrix is as follows :

(2) Perspective projection (Perspective Projection)
We think that perspective projection presents a phenomenon of near large and far small , That is, with most cameras 、 The imaging principle of the human eye is the same .
How to realize perspective projection ?
- First convert perspective projection to orthogonal projection , That is to realize the extrusion from the far plane to the near plane
- Do another orthogonal projection

How to realize extrusion from far plane to near plane ?
First, get the screen aspect ratio , And then calculate through similar triangles .


The resulting matrix is as follows :

Reference resources :
GAMES101- Introduction to modern computer graphics - Yan Lingqi _ Bili, Bili _bilibili
边栏推荐
- 简单的页面
- [cloud native] kernel security in container scenario
- Is there any discount for securities account opening? Is it safe to open an account online?
- Arlo felt lost
- 元素使用 align-items center 和 overflow auto 之后,部分内容显示不全
- 在线文本数字识别列表求和工具
- 间歇采样转发干扰
- Flask web minimalist tutorial (III) - Sqlalchemy (part a)
- 视频转图像-cv2.VideoCapture()用法
- Citation of Dissertation
猜你喜欢

How to switch to root in xshell
如何做好测试用例设计

Developers, why does the maturity of container technology herald the arrival of cloud native era?

How to create a module in the idea and how to delete a module in the idea?
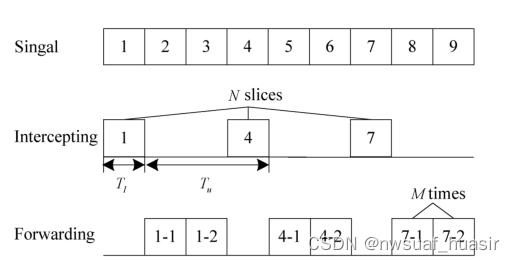
Intermittent sampling and forwarding interference

Comment personnaliser les modèles et générer rapidement le code complet dans l'idée?

How to seamlessly transition from traditional microservice framework to service grid ASM

Interviewer: how to solve the problem of massive requests for data that does not exist in redis, which affects the database?

Sofaregistry source code | data synchronization module analysis

测试用例设计方法之等价类划分方法
随机推荐
Traffic, but no sales? 6 steps to increase website sales
About the case of SQL statements
Which direction of network development is better? Data communication engineer learning path sharing
[cloud native] kernel security in container scenario
Mysql Duplicate entry ‘xxx‘ for key ‘xxx‘
UDP servers and clients in go
浮点数通信
网易云音乐内测音乐社交 App“MUS”,通过音乐匹配同频朋友
利用tsne将不同句子关于相似度可视化出来
shell 规范日期格式
Experience of C language course design: open source sharing of "push box" course design works
How to seamlessly transition from traditional microservice framework to service grid ASM
Netease cloud music beta music social app "mus" matches friends of the same frequency through music
数据库学习笔记(SQL03)
DL:深度学习模型优化之模型训练技巧总结之适时自动调整学习率实现代码
PHP wechat merchant transfer to change initiating merchant transfer API
MySQL advanced 1
IDEA工具快捷键的使用
中小企业签署ERP合同时,需要注意这几点
降低打新的预期