Study diary: February 14th, 2022

Today's first question

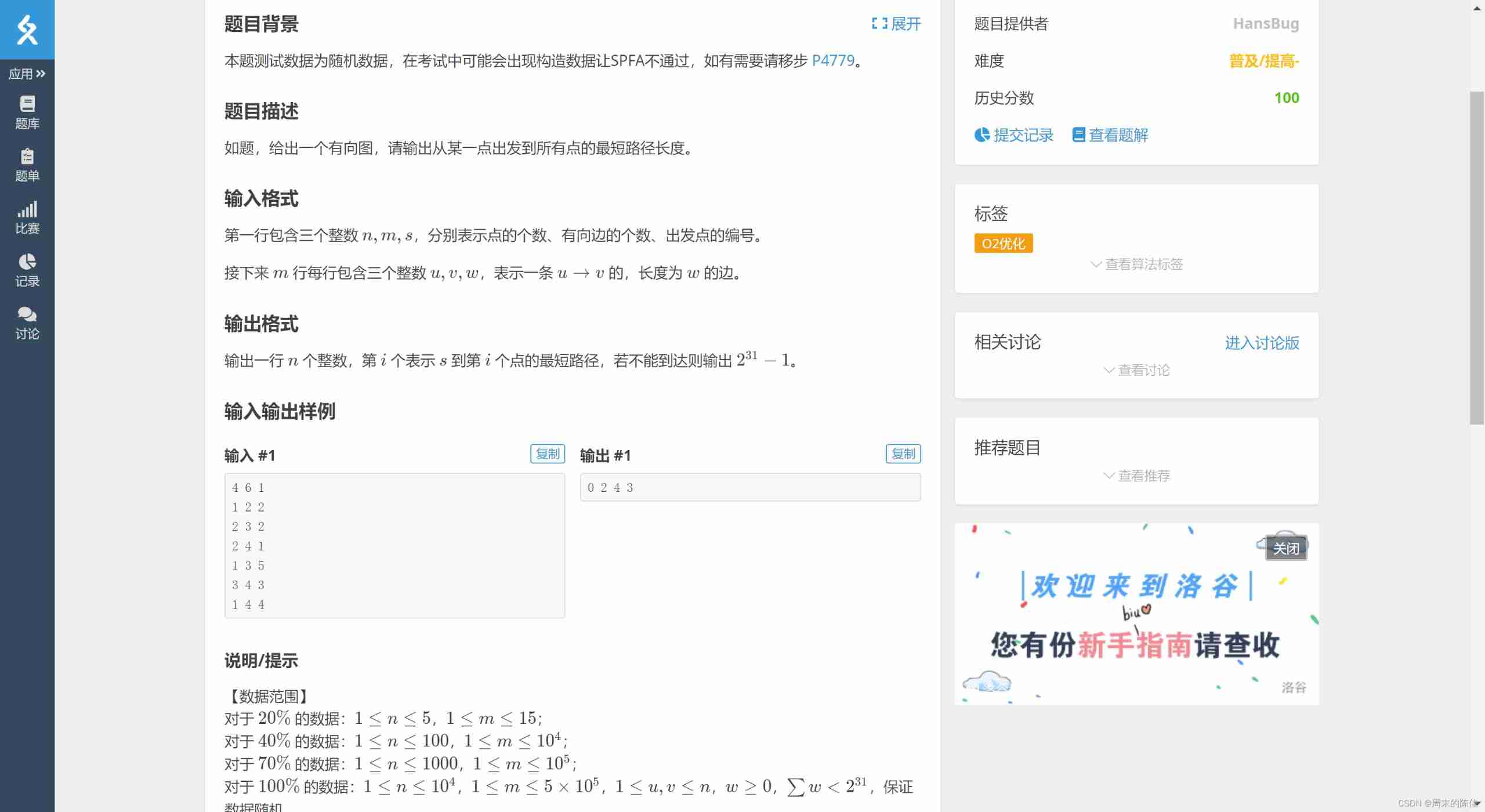
I don't know how long it tortured me , I also asked several students

The first is the storage of data .

The method used is chain forward star

The principle is similar to linked list method and adjacency list

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

Borrow the data in the title

First we define a structure

among to Store his destination

length Storage distance

next Store other nodes adjacent to it

Then define an array head

First, the first data 1 2 2

For the first structure, his to=2,length=2,next=【1】=0（ When next by 0 It indicates that there are no adjacent nodes ）

head[1]=1

Second data 2 3 2

For the second structure to=3,length=2,next=head【2】=0

head【2】=2

Third data 2 4 1

For the third structure to=4,length=1,next=head【2】=2

head【2】=3

Fourth data 1 3 5

For the fourth structure to=3,length=5,next=head【1】=1

head【1】=4

The fifth data 3 4 3

For the fifth structure to=4,length=3,next=head【3】=0;

head【3】=5

The sixth data 1 4 4

For the sixth structure to=4,length=4,next=head【4】=0;

head【4】=6;

The storage structure is similar to this

The same effect can be achieved by using linked lists

I first used a linked list

Then is the method of traversing the shortest path

  Take the figure given in the title as an example

First of all, let's start from the starting point

from 1 We can achieve 2,3,4

We also build an array to store the shortest path

because 1-1 No need to move , So the distance is 0

At first, we can start from 1-2,3,4

So we get a new table

  Then choose the shortest distance from the following table, that is 2

From the node 2 Set out to get to 3 and 4

Because what we require is the slave node 1 The shortest distance to each node ,

Let's suppose we start from 2 Transfer to 3 and 4 The distance needed is 4 and 3

It is obviously closer than the principle , So we update the form

Then from the next 3 and 4 Choose the shortest path 3, adopt 3 We can go to 4, But the distance needed is 8 Farther than the original distance , So don't change

Final selection 4, node 4 Cannot reach any node , So the final answer is

0 2 4 3

The code is as follows

#include<iostream>
using namespace std;
long long Max=2147483647;
int point,side,start;
long long result[1000000];
long long book[1000000];
struct Data
{
    int to;
    int length;
    int next;
}data[1000000];
int head[1000000];
int top=0;
int add(int a,int b,int c)
{
    top++;
    data[top].to=b;
    data[top].length=c;
    data[top].next=head[a];
    head[a]=top;
    return 0;
}
int finding(int start)
{
    for(int i=1;i<=point ;i++)
    {
        result[i]=Max;
        book[i]=0;
    }
    result[start]=0;
    int present=start;
    while(book[present]==0)
    {
        book[present]=1;
        long long mining=Max;
        for(int i=head[present];i;i=data[i].next)
        {
            if(book[data[i].to]==0)
            if(result[data[i].to]>result[present]+data[i].length)
            result[data[i].to]=result[present]+data[i].length;
        }
        for(int i=1;i<=point;i++)
        {
            if(book[i]==0)
            if(result[i]<mining)
            {
                mining=result[i];
                present=i;
            }
        }
    }
            return 0;
}

int main()
{
    cin>>point>>side>>start;
    for(int i=1;i<=side;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    finding(start);
    for(int i=1;i<=point ;i++)
    cout<<result[i]<<' ';
}

  This topic has tortured me all day

A total of submitted me 20 Time

Second question

The solution of this problem feels like brute force cracking

AHA algorithm also introduces this algorithm .

In particular, the title also gives the corresponding relationship

We also build such an array data

 

  The corresponding relationship among them , for instance data【1】【3】=1

explain 1 To 3 The degree of danger is 1

We from 1-3 There are two ways, one is directly from 1-3, Another is through the intermediate node 2

from 1 To 2 Until then 3 First, the risk of passing through the intermediate node is data【1】【2】+data【2】【3】=7. Obviously, the danger is higher , If we encounter a less dangerous one, we will exchange ,

If we want to go from 2-1 The danger level of direct arrival is 5

From the node 3 The way around is data【2】【3】+data【3】【1】=3

Less dangerous , So we put data【2】【1】 become 3; Through such comparison and transformation , Optimize all routes

The final code implementation is as follows

#include<iostream>
using namespace std;
int n,m;
int point[1000];
int data[10004][10004];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>point[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>data[i][j];   
        }
    }
    int count=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            for(int k=1;k<=n;k++)
            {
                // Choose a better route 
                if(data[j][k]>data[j][i]+data[i][k])
                {
                    data[j][k]=data[j][i]+data[i][k];
                }
            }
        }
    }
    // Take the corresponding route according to the obtained optimal route 
    for(int i=2;i<=m;i++)
    {
        count+=data[point[i-1]][point[i]];
    }
    cout<<count;
}

The algorithm used is Floyd Algorithm

Three of them are mainly used for loop , The first represents the transit node , The lower two layers are different nodes

Finally, it is better to pass the node or not , Choose the best route , Finally get the solution

The third question

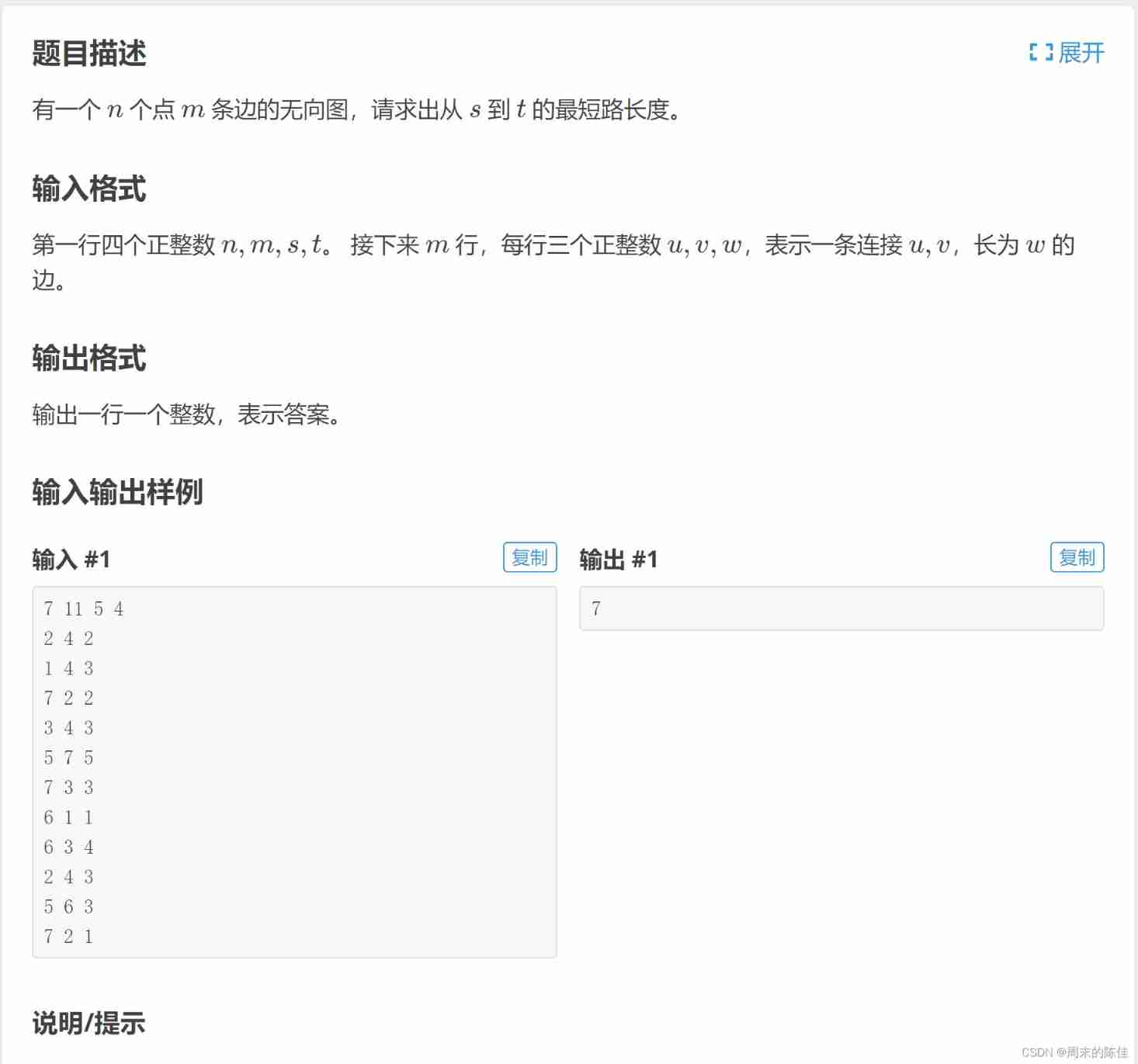
  If you remove the end point from the title and change the undirected graph into a directed graph, it will be exactly the same as the first question I wrote today

The key point is simply output result【 a key 】 That's all right. ,

What should we do when a directed graph becomes an undirected graph .

It's also very simple .

A directed graph is one that can only pass , You can't come back

An undirected graph is one that can pass , You can come back again .

Then we can add a return route based on the digraph

So I also directly modify the code of the second question a little

The final code is as follows

#include<iostream>
using namespace std;
long long Max=2147483647;
int point,side,start;
int ending;
long long result[1000000];
long long book[1000000];
struct Data
{
    int to;
    int length;
    int next;
}data[1000000];
int head[1000000];
int top=0;
int add(int a,int b,int c)
{
    top++;
    data[top].to=b;
    data[top].length=c;
    data[top].next=head[a];
    head[a]=top;
    return 0;
}
int finding(int start)
{
    for(int i=1;i<=point ;i++)
    {
        result[i]=Max;
        book[i]=0;
    }   
    result[start]=0;
    int present=start;
    while(book[present]==0)
    {
        book[present]=1;
        long long mining=Max;
        for(int i=head[present];i;i=data[i].next)
        {
            if(book[data[i].to]==0)
            if(result[data[i].to]>result[present]+data[i].length)
            result[data[i].to]=result[present]+data[i].length;
        }
        for(int i=1;i<=point;i++)
        {
            if(book[i]==0)
            if(result[i]<mining)
            {
                mining=result[i];
                present=i;
            }
        }
    }
            return 0;
}

int main()
{
    cin>>point>>side>>start>>ending;
    for(int i=1;i<=side;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
    }
    finding(start);
    cout<<result[ending];
}

The core code and central idea have basically not changed

Fourth question

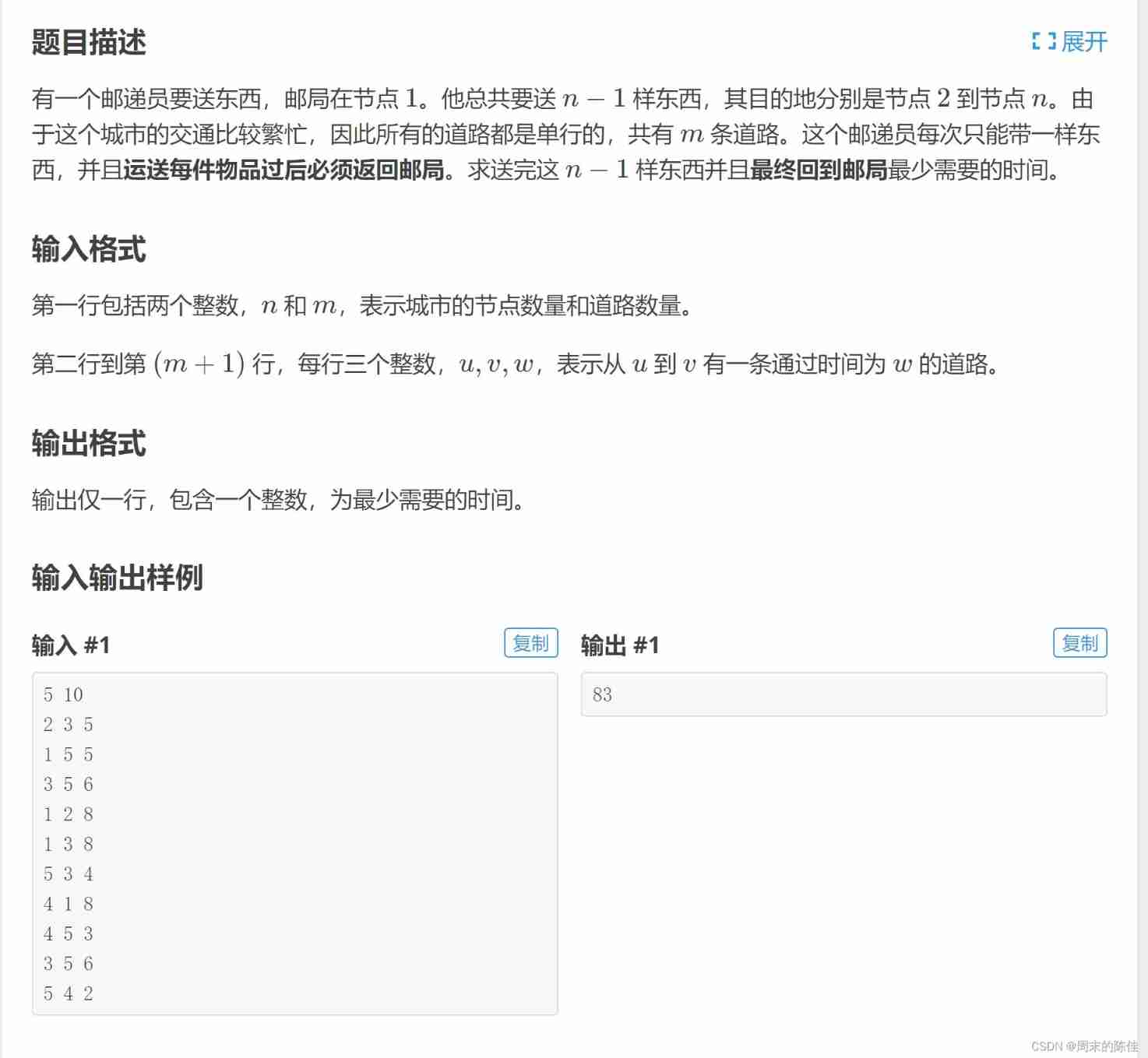
This question is also a variant of the Pirates of the Caribbean

It's just a little troublesome , There are going and coming back

If yes data[i][j] If it comes back data[j][i]
The final code is as follows

#include<iostream>
using namespace std;
int n,m;
int data[1003][1003];
int main()
{
    cin>>n>>m;
    
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            data[i][j]=99999999;
        }
    }
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        data[a][b]=min(data[a][b],c);
    }
    long long count=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            for(int k=1;k<=n;k++)
            {
                if(data[j][k]>data[j][i]+data[i][k])
                {
                    data[j][k]=data[j][i]+data[i][k];
                }
            }
        }
    }
    for(int i=2;i<=n;i++)
    {
        count+=data[1][i]+data[i][1];
    }
    cout<<count;
}

Among them, we need to think about repeating edges a little , It may be a road and a path , Choose the shortest way