当前位置:网站首页>Shortest path problem of graph theory (acwing template)
Shortest path problem of graph theory (acwing template)
2022-07-03 20:12:00 【lihua777】
Catalog
Example :Dijkstra Find the shortest path
Heap optimized dijkstra Algorithm
Example :Dijkstra Find the shortest path Ⅱ
Bellman-Ford Algorithm ( Dealing with graphs with negative weighted edges )
Example : The shortest path with limited number of edges
spfa Algorithm (Bellman-Ford Algorithm queue Optimization Algorithm )
Floyd Algorithm ( Multi source shortest path )
A term is used to explain :n: Usually represents points m: Usually represents the number of sides
Source : The starting point Single source : A starting point Multi-source : Multiple starting points
Confluence : End
The degree of : How many sides point to me
The degree of : The number of sides going out from this point
Border right : In discrete mathematics or data structures , A numerical value of each edge band of a graph , The meaning he represents can be length and so on , This value is the edge weight
Frame diagram :

Simple Dijkstra Algorithm :
Because its time complexity is O(N^2) The number of edges is independent of time complexity , So it is suitable for dense graphs
A dense picture : The number of sides is the number of points 2~3 times
ACwing Notes for the whole course of basic algorithm course (2021 year 8 month 12 Rewrite on the th + Optimize )_hebtu_Kangweiqi The blog of -CSDN Blog _acwing note Basic algorithm Course Notes , Please support genuine https://blog.csdn.net/hebtu_Kangweiqi/article/details/109124329 Borrow the big guy's picture = =
Dijkstra Templates :

Example :Dijkstra Find the shortest path
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , All edge weights are positive .
Please find out 1 It's on the n The shortest distance of point No , If you can't get from 1 Go to No n Number point , The output -1
Thinking analysis : I feel greedy , Every time I choose the one with the smallest distance from me , Then most 1~j The shortest distance becomes
1~t Distance of points t~j The shortest distance
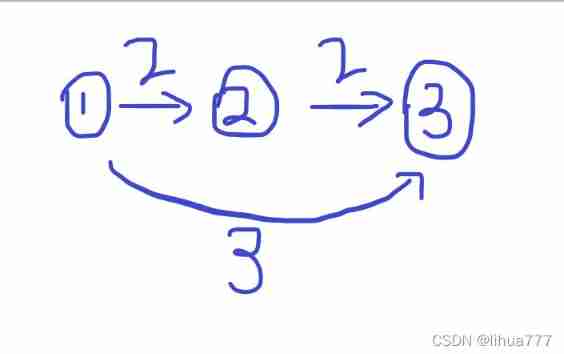
I suggest you look at the code and simulate it on the diagram , You will feel the beauty of this algorithm !!!
#include<iostream>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];// Adjacency matrix is used to store
int dist[N];// Distance array
bool st[N];// Judge array
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);// The value of the initialization array is a large number 1e9
dist[1] = 0;// Will be the first 1 The distance from point No. to itself is initialized to 0
for (int i = 0; i < n; i++)
{//n Sub iteration
int t = -1;// Just a meaningless number : The purpose is to find out 2~n Inner distance point 1 Minimum number
for (int j = 1; j <= n; j++)// from 1 To traverse the : Pay attention to this detail
{
if (!st[j] && (t == -1 || dist[j] < dist[t]))// If the point has not been passed
{
t = j;// It is equivalent to finding the minimum value 1~1 1~2
}
}
st[t] = 1;// The mark has been used at this point
for (int j = 1; j <= n; j++)// Traverse 1 It's on the n Number point
{// Update distance
dist[j] = min(dist[j], dist[t] + g[t][j]);//1~j The distance between points becomes :1~t Distance of +t~j Distance of
}
}
if (dist[n] == 0x3f3f3f3f) return -1;// If n Point arrays have not been used , Then prove that you can't go n spot
else return dist[n];
}
int main() {
cin >> n >> m;
memset(g, 0x3f, sizeof g);
while (m--)
{
int x, y, z;//x~y The distance to z
cin >> x >> y >> z;
g[x][y] = min(g[x][y], z);
}
int t = dijkstra();
printf("%d\n", t);
return 0;
}
Heap optimized dijkstra Algorithm

Through the analysis of the above figure : We can 2 Of (1)(3) Optimize with heap to reduce time complexity , But the variable of the number of edges will be introduced , So heap optimized dijkstra Version is suitable for sparse drawings
Example :Dijkstra Find the shortest path Ⅱ
problem :
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , All edge weights are nonnegative .
Please find out 1 It's on the n The shortest distance of point No , If you can't get from 1 Go to No n Number point , The output -1.
For sparse graphs , We use adjacency table
Code implementation :
#include<iostream>
#include <queue>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int, int> PII;
int h[N], e[2 * N], ne[2 * N], w[N], idx;// Adjacency list + Weight array
int n, m;// points + Number of edges
int dist[N];// Distance array
bool st[N];// Judge array
void add(int a, int b, int c)
{
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);// The initialization distance is a large number
dist[1] = 0;//1 The distance to oneself is 0
priority_queue<PII, vector<PII>, greater<PII> >heap;// Build a little root pile ( Priority queue )
heap.push({ 0,1 });// Into the heap
while (heap.size())// When the queue is not empty
{
auto t = heap.top();// Take the head
heap.pop();// Truncate
int ver = t.second, distance = t.first;//first: distance ,ver: Number of nodes
if (st[ver]) continue;// If the node has been marked , I will not go
st[ver] = 1;// Tag nodes
for (int i = h[ver]; i != -1; i = ne[i])// Traversal of adjacency table
{
int j = e[i];// Get the number of nodes
if (dist[j] > distance + w[i])// Find the minimum distance
{
dist[j] = distance + w[i];// node 1 To node of j The distance of is the distance of the head node + Its weight ( Side length )
heap.push({ dist[j],j });// Into the heap
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while (m--)
{
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
}
cout << dijkstra();
}
Bellman-Ford Algorithm ( Dealing with graphs with negative weighted edges )
1、 What is? bellman - ford Algorithm ?
Bellman - ford The algorithm is an algorithm for finding the shortest path of a single source with a negative weight graph , Low efficiency , The code is less difficult . The principle is continuous relaxation , Update each edge every time you relax , If in n-1 It can be renewed after relaxation , Then it shows that there is a negative ring in the figure , Therefore, no results can be obtained , Otherwise, complete .
( Generally speaking, it's : hypothesis 1 It's on the n Point number is accessible , Every point starts in the same direction , Update the shortest distance between adjacent points , Through the loop n-1 operations , If there is no negative ring in the graph , be 1 Point number is bound to arrive n Number point , If there is a negative ring in a graph , It's in n-1 It's bound to be updated after a second relaxation )
2、bellman - ford The specific steps of the algorithm
for n Time
for All sides a,b,w ( Slack operation )
dist[b] = min(dist[b],back[a] + w)
Be careful :back[] The array is after the last iteration dist[] Backup of array , Because every point starts out at the same time , So you need to dist[] Array for backup , If you don't do a backup, there will be a cascading effect , To the next point
3、 In the following code , Whether we can reach n In the judgment of No if(dist[n] > INF/2) Judge , It is not. if(dist[n] == INF) Judge , as a result of INF It's a definite value , It's not really infinity , Will be affected by other values ,dist[n] Greater than one with INF The same order of magnitude
4、bellman - ford The algorithm is good at solving the shortest path problem with limited number of edges
Time complexity O ( n m ) O(nm)O(nm)
among n For points ,m Number of sides
————————————————
Copyright notice : This paper is about CSDN Blogger 「 Cloud algorithm 」 The original article of , follow CC 4.0 BY-SA Copyright agreement , For reprint, please attach the original source link and this statement .
Link to the original text :https://blog.csdn.net/hebtu_Kangweiqi/article/details/109124329
Example : The shortest path with limited number of edges
problem :
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , The edge weight may be negative .
Please find out from 1 It's on the n The maximum passage of point No k The shortest distance of the edge , If you can't get from 1 Go to No n Number point , Output impossible Be careful : Possible in the figure There is a negative weight loop
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 50;
int n, m, k;
int dis[N], backup[N];
struct edge { int a, b, w; } e[N];
void bellman()
{
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
for (int i = 0; i < k; i ++)// At most k side
{
memcpy(backup, dis, sizeof dis);// Update every time with the last status
for (int j = 1; j <= m; j ++)
{
int a = e[j].a, b = e[j].b, w = e[j].w;
dis[b] = min(dis[b], backup[a] + w);// To b The distance between points is equal to a Point distance plus side length
}
}
}
int main()
{
cin >> n >> m >> k;
for (int i = 1; i <= m; i ++)
cin >> e[i].a >> e[i].b >> e[i].w;
bellman();
// Whether we can reach n In the judgment of No if(dist[n] > INF/2) Judge , It is not. if(dist[n] == INF) Judge , as a result of INF It's a definite value , It's not really infinity , Will be affected by other values ,dist[n] Greater than one with INF The same order of magnitude
if (dis[n] > 0x3f3f3f3f / 2) puts("impossible");
else cout << dis[n] << endl;
return 0;
}
spfa Algorithm (Bellman-Ford Algorithm queue Optimization Algorithm )
spfa Algorithm steps
queue <– 1
while queue Not empty
(1) t <– Team head
queue.pop()
(2) use t Update all outgoing edges t –> b, A weight of w
queue <– b ( If the point has been updated , Use this point to update other points )Time complexity commonly :O ( m ) The worst :O ( n m )
n For points ,m Number of sides
3、spfa It can also solve the shortest distance problem of graphs with positive weights , And in general, it's better than Dijkstra The algorithm is OK
————————————————
Copyright notice : This paper is about CSDN Blogger 「 Cloud algorithm 」 The original article of , follow CC 4.0 BY-SA Copyright agreement , For reprint, please attach the original source link and this statement .
Link to the original text :https://blog.csdn.net/hebtu_Kangweiqi/article/details/109124329
problem :
The shortest path with limited number of edges
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , The edge weight may be negative .
Please find out from 1 It's on the n The maximum passage of point No k The shortest distance of the edge , If you can't get from 1 Go to No n Number point , Output impossible.
Be careful : Possible in the figure There is a negative weight loop .
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e5 + 5;
int n, m, dis[N];
bool st[N];// Whether the representative point is in the queue
int h[N], e[N], ne[N], w[N], idx;// Single chain list
void add(int a, int b, int c)// Insert operation of single chain table
{
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
int spfa()
{
queue<int> q;
memset(dis, 0x3f, sizeof dis);
q.push(1);// Put in node 1
dis[1] = 0;// A distance of 1
st[1] = 1;// Judge
while (!q.empty()) // The queue is not empty
{
int u = q.front();// Take out the head
q.pop();// Truncate
st[u] = 0;// Mark
for (int i = h[u]; i != -1; i = ne[i])// Traversing the linked list
{
int v = e[i];// Take out node
if (dis[v] > dis[u] + w[i])// For the minimum
{
dis[v] = dis[u] + w[i];
if (!st[v]) // If not
{
q.push(v);// Put in
st[v] = 1;// Mark
}
}
}
}
if (dis[n] == 0x3f3f3f3f) return -1;
else return dis[n];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
while (m--) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
}
int t = spfa();
if (t == -1) puts("impossible");
else printf("%d", t);
}
spfa Find the negative ring
problem :
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , The edge weight may be negative
Please judge whether there is a negative weight circuit in the figure
#include<iostream>
#include<queue>
using namespace std;
const int N = 2005, M = 10005;
int h[N], e[M], ne[M], w[M], idx, n, m;
int dis[N], cnt[N];// Need an extra cnt Array , Record the number of sides on the shortest path at the current point
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
bool spfa()
{
/* First of all, the distance does not need to be initialized */
queue<int> q;
/* Join all points in the team , It can prevent some points from going to the negative ring */
for (int i = 1; i <= n; i++)
{
q.push(i);
st[i] = 1;
}
while (!q.empty())
{
int u = q.front();
q.pop();
st[u] = 0;
for (int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if (dis[v] > dis[u] + w[i])
{
dis[v] = dis[u] + w[i];
cnt[v] = cnt[u] + 1;
if (cnt[v] >= n) return 1;
/* If exceeded n, According to the drawer principle , The number of points passed in the middle must be greater than n,*/
if (!st[v]) {
q.push(v);
st[v] = 1;
}
}
}
}
return 0;
}
int main() {
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
}
if (spfa()) puts("Yes");
else puts("No");
}
Floyd Algorithm ( Multi source shortest path )
problem :
Given a n A little bit m Directed graph of strip edge , There may be double edges and self rings in the graph , The edge weight may be negative .
Re given k A asked , Each query contains two integers x and y, Indicates that the query is from point x point-to-point y The shortest distance , If the path doesn't exist , The output “impossible”.
There is no negative weight loop in the data assurance diagram
#include<iostream>
using namespace std;
const int N = 210;
const int inf = 0x3f3f3f3f;
int n, m, q;
int d[N][N];
void floyd() {
for (int k = 1; k <= n; k++)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &q);
/* initialization */
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j) d[i][j] = 0;
else d[i][j] = inf;
}
}
while (m--)
{
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
d[x][y] = min(d[x][y], z);// Pay attention to the double edge
}
floyd();
while (q--) //q Time to ask
{
int x, y;
scanf("%d%d", &x, &y);
if (d[x][y] > inf / 2) puts("impossible");// The problem may appear negative weight side , So we need to apply the previous routine
else printf("%d\n", d[x][y]);
}
return 0;
}
边栏推荐
- PR 2021 quick start tutorial, how to create a new sequence and set parameters?
- Battle drag method 1: moderately optimistic, build self-confidence (1)
- BOC protected tryptophan zinc porphyrin (Zn · TAPP Trp BOC) / copper porphyrin (Cu · TAPP Trp BOC) / cobalt porphyrin (cobalt · TAPP Trp BOC) / iron porphyrin (Fe · TAPP Trp BOC) / Qiyue supply
- Make a simple text logo with DW
- Fingerprint password lock based on Hal Library
- 6. Data agent object Defineproperty method
- 2.3 other data types
- Day10 -- forced login, token refresh and JWT disable
- Global and Chinese market of charity software 2022-2028: Research Report on technology, participants, trends, market size and share
- Microservice knowledge sorting - search technology and automatic deployment technology
猜你喜欢
2.4 conversion of different data types
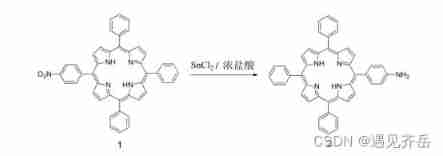
5- (4-nitrophenyl) - 10,15,20-triphenylporphyrin ntpph2/ntppzn/ntppmn/ntppfe/ntppni/ntppcu/ntppcd/ntppco and other metal complexes
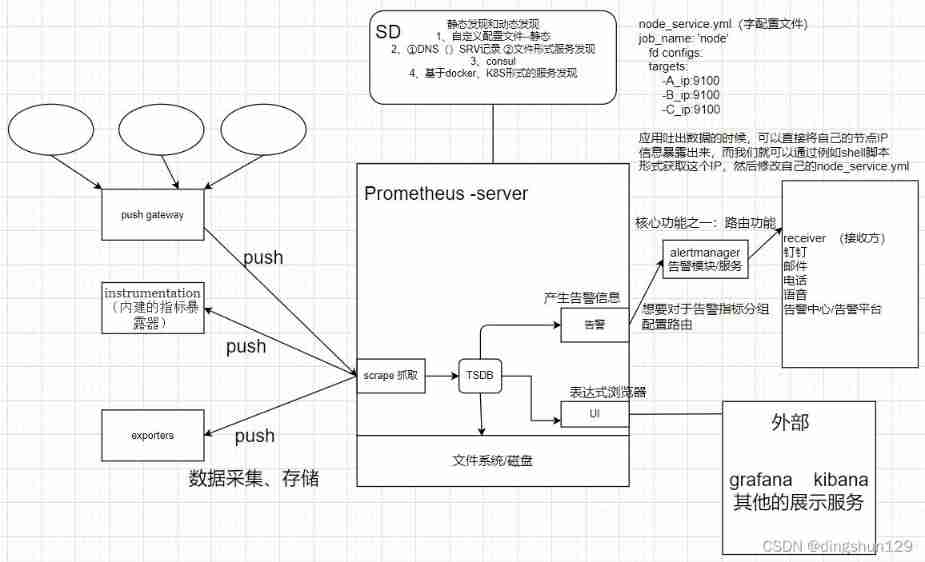
Promethus
Popularize the basics of IP routing

10 smart contract developer tools that miss and lose
PR 2021 quick start tutorial, material import and management
JMeter connection database

MPLS configuration
BOC protected tryptophan porphyrin compound (TAPP Trp BOC) Pink Solid 162.8mg supply - Qiyue supply
![2022 - 06 - 30 networker Advanced (XIV) Routing Policy Matching Tool [ACL, IP prefix list] and policy tool [Filter Policy]](/img/b6/5d6b946d8001e2d73c2cadbdce72fc.png)
2022 - 06 - 30 networker Advanced (XIV) Routing Policy Matching Tool [ACL, IP prefix list] and policy tool [Filter Policy]
随机推荐
About unregistered transfer login page
Sword finger offer 30 Stack containing min function
Global and Chinese market of liquid antifreeze 2022-2028: Research Report on technology, participants, trends, market size and share
BOC protected alanine porphyrin compound TAPP ala BOC BOC BOC protected phenylalanine porphyrin compound TAPP Phe BOC Qi Yue supply
Unittest framework is basically used
The simplicity of laravel
Meso tetra [P - (p-n-carbazole benzylidene imino)] phenylporphyrin (tcipp) /eu (tcipp) [pc( α- 2-oc8h17) 4] and euh (tcipp) [pc (a-2-oc8h17) 4] supplied by Qiyue
Bool blind note - score query
Test changes in Devops mode -- learning and thinking
Microservice framework - frequently asked questions
Global and Chinese markets of lithium chloride 2022-2028: Research Report on technology, participants, trends, market size and share
Geek Daily: the system of monitoring employees' turnover intention has been deeply convinced off the shelves; The meta universe app of wechat and QQ was actively removed from the shelves; IntelliJ pla
Teach you how to quickly recover data by deleting recycle bin files by mistake
1.5 learn to find mistakes first
Bright purple crystal meso tetra (4-aminophenyl) porphyrin tapp/tapppt/tappco/tappcd/tappzn/tapppd/tappcu/tappni/tappfe/tappmn metal complex - supplied by Qiyue
Global and Chinese market of electrolyte analyzers 2022-2028: Research Report on technology, participants, trends, market size and share
Initialization and instantiation
FPGA learning notes: vivado 2019.1 project creation
What is the difference between a kill process and a close process- What are the differences between kill process and close process?
How to check the permission to write to a directory or file- How do you check for permissions to write to a directory or file?