LeetCode 最大矩形，最大正方形系列 84. 85. 221. 1277. 1725. （单调栈，动态规划）

84.柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

输入：heights = [2,1,5,6,2,3]
输出：10

思路

遍历每个柱子，每次算出以当前柱子高度作为矩形的高，往左右两侧扩展，能够得到的最大矩形。再对每个柱子得到的矩形取个最大值即可。

某个柱子往左右两侧扩展，最多能扩展到什么地方呢？自然是遇到第一个比自己更低的柱子，就无法再扩展下去了。于是我们的问题变成了，对于每个柱子，求一下其左侧第一个比它低的柱子，再求一下其右侧第一个比它低的柱子，这两个柱子之间的距离，就是能够扩展的最大的矩形的宽。

于是问题就变成了，在一个数组中，求解每个数左侧第一个比它小的数。

对于这种求左侧（右侧）第一个比自己小（大）的问题，都是单调栈的经典应用。

来看下单调栈为什么能够起到作用。假设是求第i个数左侧第一个比自己小的数。

我们从位置i往左走，如果遇到一个数a，这个数比更左侧的所有数都小。那么对于位置i，其答案不可能取到数a更左侧的位置，因为数a左边那些比a大的数，都被a这个数给挡住了。

所以我们能知道一个结论：从右往左走时，先遇到的较小的数，会把后面的更大的数全部挡住，使得更左侧的更大的数不可能作为答案。只有更左侧且更小的数，才可能作为答案。

所以我们从左往右遍历，求解每个数左侧第一个比它小的，只要维护一个单调栈，栈中的数单调递增。

每次求解当前位置答案时，依次弹出栈顶，直到栈顶元素小于当前元素，则此时栈顶就是当前位置的答案，并把当前位置入栈，保持栈内的单调递增。

求解右侧第一个比自己小的数，同理，将遍历顺序反过来即可。

求解第一个比自己大的数也是类似，更早出现的更大的数，会把后面的更小的数全部挡住。不再赘述。

下面给出代码，注意单调栈里存的是下标，因为我们需要计算两根柱子之间的距离，但我们需要按照柱子的高度递增来维护单调栈。

class Solution {
    
    // 核心思路是, 对于每个柱子, 看其能往左往右扩展多少
    // 需要找到其左侧和右侧第一个比它低的柱子
    public int largestRectangleArea(int[] heights) {
    
        int n = heights.length;
        int[] stack = new int[n];
        int top = -1;
        int[] left = new int[n]; // 每个位置左侧第一个比自己低的柱子的位置
        int[] right = new int[n]; // 每个位置右侧第一个比自己低的柱子的位置

        for (int i = 0; i < n; i++) {
    
            // 栈非空, 且栈顶柱子高度比当前柱子高度大, 则弹出栈顶
            while (top >= 0 && heights[stack[top]] >= heights[i]) top--;
            left[i] = top >= 0 ? stack[top] : -1;
            stack[++top] = i;
        }

        top = -1; // clear the stack
        
        for (int i = n - 1; i >= 0; i--) {
    
            while (top >= 0 && heights[stack[top]] >= heights[i]) top--;
            right[i] = top >= 0 ? stack[top] : n;
            stack[++top] = i;
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
    
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

85.最大矩形

题目描述

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如下图所示。

思路

求解的是最大矩形。我们先想一个最直观的做法，那就是枚举所有可能的矩形，并计算每个矩形的面积。怎么来枚举矩形呢？一个矩形由2个点就可以唯一确定，即左上角的点和右下角的点。

我们不妨枚举这个二维矩阵的每个点[x,y]，把每个点作为矩形的右下角，尝试找到所有以这个点为右下角的矩形。

那么，只有当这个点为1时，才能至少构成一个矩形。我们尝试找以这个点为右下角的矩形时，一定是要向上和向左扩展的。

我们不妨就只向上扩展。而对于向左扩展，我们预处理出每个点左侧连续1的个数这样的信息，不妨设其为left[x][y]。

我们称往左扩展的是矩形的宽，往上扩展是矩形的高。

我们是向上扩展的，初始时，矩形的高为1，此时往左扩展最远到left[x][y]，此时就能求出以[x,y]为右下角，高为1的矩形的最大面积。再往上扩展，矩形高为2，此时矩形的宽为min(left[x][y], left[x + 1][y])；能够求出高为2的矩形的最大面积；

继续往上扩展，高为3，宽为min(left[x][y], left[x + 1][y], left[x + 2][y])。后面同理。

直到无法往上扩展为止。

根据这个思路，写出代码如下：

class Solution {
    
    public int maximalRectangle(char[][] matrix) {
    
        int n = matrix.length, m = matrix[0].length;
        int[][] left = new int[n][m]; // 每个点左侧连续1的个数
        for (int i = 0; i < n; i++) {
    
            int len = 0;
            for (int j = 0; j < m; j++) {
    
                if (matrix[i][j] == '1') len++;
                else len = 0;
                left[i][j] = len;
            }
        }

        int ans = 0;
        for (int i = 0; i < n; i++) {
    
            for (int j = 0; j < m; j++) {
    
                if (matrix[i][j] == '0') continue;
                int width = left[i][j];
                for (int k = i; k >= 0; k--) {
    
                    if (matrix[k][j] == '0') break; // 无法向上扩展了
                    width = Math.min(width, left[k][j]); // 更新宽度
                    ans = Math.max(ans, width * (i - k + 1)); // 计算矩形面积
                }
            }
        }
        return ans;
    }
}

预处理左侧连续1的个数，时间复杂度 $O(n\times m)$，对于每个点作为矩形右下角，向上扩展找到全部矩形，时间复杂度 $O(n\times m\times n)$，总时间复杂度为$O(n\times n\times m)$

优化

根据上面的思路，我们容易发现，由于我们对每个点是往上扩展。我们可以将每一列拿出来单独看，由于每个点预处理了其左侧连续1的个数。对于某一列，这一列上每个点左侧连续1的个数，就可以看作柱子的高度，只不过这些柱子是以当前列为基线，往左侧生长的。

所以，我们单独看每一列时，其实就是求解第84题了。于是可以套用84题单调栈的解法。对于每一列，求解的复杂度为$O(n)$，一共有m列，所以总复杂度为$O(n\times m)$

class Solution {
    
    public int maximalRectangle(char[][] matrix) {
    
        int n = matrix.length, m = matrix[0].length;
        int[][] left = new int[n][m]; // 左侧连续1的个数
        for (int i = 0; i < n; i++) {
    
            int len = 0;
            for (int j = 0; j < m; j++) {
    
                if (matrix[i][j] == '1') len++;
                else len = 0;
                left[i][j] = len;
            }
        }
        int[] stack = new int[n];
        int top = -1;
        int ans = 0;
        int[] down = new int[n]; // 每一列下侧第一个比当前位置小的
        int[] up = new int[n]; // 每一列上侧第一个比当前位置小的
        for (int i = 0; i < m; i++) {
    
            top = -1; // clear stack
            for (int j = n - 1; j >= 0; j--) {
    
                while (top >= 0 && left[j][i] <= left[stack[top]][i]) top--;
                down[j] = top >= 0 ? stack[top] : n;
                stack[++top] = j;
            }
            top = -1; // clear stack
            for (int j = 0; j < n; j++) {
    
                while (top >= 0 && left[j][i] <= left[stack[top]][i]) top--;
                up[j] = top >= 0 ? stack[top] : -1;
                stack[++top] = j;
            }

            for (int j = 0; j < n; j++) {
    
                ans = Math.max(ans, (down[j] - up[j] - 1) * left[j][i]);
            }
        }
        return ans;
    }
}

221.最大正方形

上面求解的是最大矩形，现在来看一下一道类似的题目，最大正方形

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

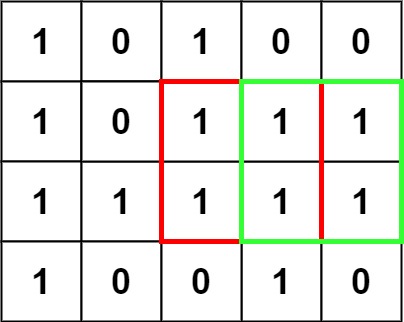
思路

同样的，我们考虑一个正方形可以怎么表示。和矩形用左上和右下两个顶点表示不同，我们可以只用一个顶点，加上边长，来表示一个正方形。所以我们考虑，枚举二维矩阵中的每个点，找到以这个点为右下角的最大的正方形。

与上面求最大矩形不同。这道题用DP来做。

我们设f(i,j)来表示，以[i,j]为右下角的最大正方形的边长。

我们以[i,j]为右下角，找最大正方形，则要看其往上和往左，能延申的最长长度。观察可以发现， 以[i,j]为右下角的最大正方形的边长，会受制于以[i - 1, j]，以[i, j - 1]，以[i - 1, j - 1]为右下角的最大正方形的边长。于是得到状态转移方程

f[i][j] = min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1

我们来证明一下这个状态转移方程的正确性。

假设f[i][j] = k，则f[i - 1][j]至少为k - 1，f[i][j - 1]也至少为k - 1，f[i - 1][j - 1]也至少为k - 1，于是容易得出

min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) >= k - 1

即min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1 >= f[i][j]

接下来只要证一下>关系是不成立的即可。

若min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1 > f[i][j]

则f[i - 1][j] > f[i][j] - 1

f[i][j - 1] > f[i][j] - 1

f[i - 1][j - 1] > f[i][j] - 1

即

f[i - 1][j] >= f[i][j]

f[i][j - 1] >= f[i][j]

f[i - 1][j - 1] >= f[i][j]

画个图可以得到，当这个条件成立时，f[i][j]能够取到的最大值至少是k + 1，而不是k，这就与先前的假设矛盾了。所以>关系一定不成立，进而有f[i][j] = min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1

class Solution {
    
    public int maximalSquare(char[][] matrix) {
    
        int n = matrix.length, m = matrix[0].length;
        int[][] f = new int[n + 1][m + 1];
        int ans = 0;
        for (int i = 1; i <= n; i++) {
    
            for (int j = 1; j <= m; j++) {
    
                if (matrix[i - 1][j - 1] == '1') {
    
                    // 三者取最小
                    f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]);
                    f[i][j] = Math.min(f[i][j], f[i - 1][j - 1]);
                    // 加一
                    f[i][j]++;
                    ans = Math.max(ans, f[i][j]);
                }
            }
        }
        return ans * ans; // 要求的是面积
    }
}

由于每个状态只依赖于左，上，左上，这三个状态，可以用滚动数组进行空间上的优化

class Solution {
    
    public int maximalSquare(char[][] matrix) {
    
        int n = matrix.length, m = matrix[0].length;
        int[] f = new int[m + 1];
        int ans = 0;
        for (int i = 1; i <= n; i++) {
    
            int topLeft = 0; // 左上角
            for (int j = 1; j <= m; j++) {
    
                if (matrix[i - 1][j - 1] == '1') {
    
                    // 三者取最小
                    int temp = f[j]; // 暂存, 作为下一轮迭代的左上角
                    f[j] = Math.min(f[j], f[j - 1]);
                    f[j] = Math.min(f[j], topLeft);
                    // 加一
                    f[j]++;
                    ans = Math.max(ans, f[j]);
                    topLeft = temp;
                } else {
    
                    f[j] = 0; //如果当前位置不是1, 则要更新为0
                }
            }
        }
        return ans * ans; // 要求的是面积
    }
}

1277.统计全为1的正方形子矩阵

题目描述

给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。

思路

和221的思路一样，221我们用f[i][j]维护了最大正方形的边长，而以[i,j]为右下角的正方形的个数，就等于最大正方形的边长。

最终的答案把所有的f[i][j]做一下累加即可

class Solution {
    
    public int countSquares(int[][] matrix) {
    
        int n = matrix.length, m = matrix[0].length;
        int[][] f = new int[n + 1][m + 1];
        int ans = 0;
        for (int i = 1; i <= n; i++) {
    
            for (int j = 1; j <= m; j++) {
    
                if (matrix[i - 1][j - 1] == 1) {
    
                    f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]);
                    f[i][j] = Math.min(f[i][j], f[i - 1][j - 1]) + 1;
                    ans += f[i][j];
                }
            }
        }
        return ans;
    }
}

1725.可以形成最大正方形的矩阵数目

题目描述

给你一个数组 rectangles ，其中 rectangles[i] = [li, wi] 表示第 i 个矩形的长度为 li 、宽度为 wi 。

如果存在 k 同时满足 k <= li 和 k <= wi ，就可以将第 i 个矩形切成边长为 k 的正方形。例如，矩形 [4,6] 可以切成边长最大为 4 的正方形。

设 maxLen 为可以从矩形数组 rectangles 切分得到的 最大正方形 的边长。

请你统计有多少个矩形能够切出边长为 maxLen 的正方形，并返回矩形 数目 。

思路

维护最大正方形的边长，并进行累加即可。当出现了更大的正方形，则将累加的数目重置。

class Solution {
    
    public int countGoodRectangles(int[][] rectangles) {
    
        int maxLen = 0, cnt = 0;
        for (int[] r : rectangles) {
    
            // 该矩形能切出的最大正方形
            int len = Math.min(r[0], r[1]);
            if (maxLen == len) cnt++; // 如果等于最大正方形, 则累加
            else if (maxLen < len) {
    
                // 否则, 出现了更大的正方形, 计数重置
                maxLen = len;
                cnt = 1;
            }
        }
        return cnt;
    }
}