The counting tool of combinatorial mathematics -- generating function

The generating function is like a function but not a function .

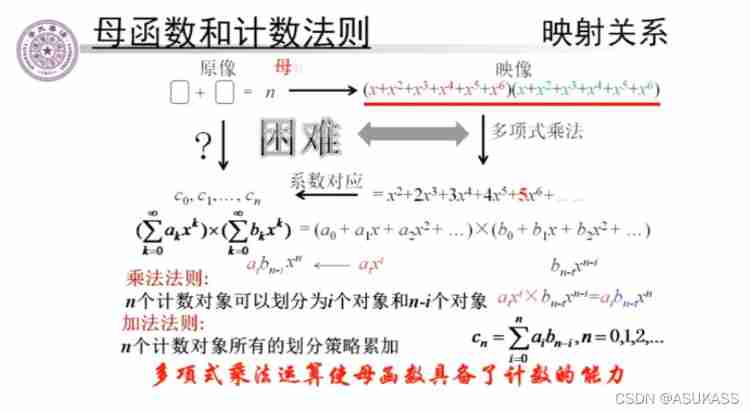
Understand that the dice model can be used here , That is, two dice are rolled 6 How many times do you click ：

Divide the two dice into one dice by rolling them step by step , The probability of a single die rolling a point is x, Two things are x*x, Then the probability distribution of a single dice according to the law of addition is x+x square .......+x Sixth power , Two dice because it is a step-by-step process , So we should let two polynomials （ The generating function ） Multiply , In the sum polynomial x The coefficient before the sixth power is 6 The number of times a dot appears .

In the same way m The dice roll n What is the probability of a point .

Simple application of generating function ;

 

 

Here is my brief understanding of the problem ：

In fact, this problem is to divide the four weights into four steps according to the step-by-step division strategy , first 1 There are two possibilities for Gram's weight to be weighed or not , The probability of a gram is x,0 Gram is x To the zeroth power of 1, Because these two possibilities are in the same step , So add up . In the same way, we know that the generating function of two grams of weight is 1+x square ....... And so on , Calculate the generating functions of the four weights and multiply them  , In the resulting generating function polynomial ,x The number of times is a few grams , The coefficient in front of it is the number of schemes .