当前位置:网站首页>迭代扩展卡尔曼滤波IEKF
迭代扩展卡尔曼滤波IEKF
2022-08-03 23:58:00 【威士忌燕麦拿铁】
迭代扩展卡尔曼滤波IEKF
预测
迭代扩展卡尔曼滤波(IEKF)的预测部分和扩展卡尔曼滤波基本相同。直接给出结论:
x ˇ k = f ( x ^ k − 1 , v k , 0 ) \check{\boldsymbol{x}}_{k} =\boldsymbol{f}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \mathbf{0}\right) xˇk=f(x^k−1,vk,0)
P ˇ k = F k − 1 P ^ k − 1 F k − 1 T + Q k ′ \check{\boldsymbol{P}}_{k} =\boldsymbol{F}_{k-1} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k-1}^{\mathrm{T}}+\boldsymbol{Q}_{k}^{\prime} Pˇk=Fk−1P^k−1Fk−1T+Qk′
更新
非线性观测模型为:
y k = g ( x k , n k ) \boldsymbol{y}_{k}=g\left(\boldsymbol{x}_{k}, \boldsymbol{n}_{k}\right) yk=g(xk,nk)
对其中任意一个点 x o p , k \boldsymbol{x}_{\mathrm{op}, k} xop,k 进行线性化,可得:
g ( x k , n k ) ≈ y o p , k + G k ( x k − x o p , k ) + n k ′ \boldsymbol{g}\left(\boldsymbol{x}_{k}, \boldsymbol{n}_{k}\right) \approx \boldsymbol{y}_{\mathrm{op}, k}+\boldsymbol{G}_{k}\left(\boldsymbol{x}_{k}-\boldsymbol{x}_{\mathrm{op}, k}\right)+\boldsymbol{n}_{k}^{\prime} g(xk,nk)≈yop,k+Gk(xk−xop,k)+nk′
其中:
- y o p , k = g ( x o p , k , 0 ) \boldsymbol{y}_{\mathrm{op}, k}=\boldsymbol{g}\left(\boldsymbol{x}_{\mathrm{op}, k}, \mathbf{0}\right) yop,k=g(xop,k,0)
- G k = ∂ g ( x k , n k ) ∂ x k ∣ x o p , k , 0 \boldsymbol{G}_{k}=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_{k}, \boldsymbol{n}_{k}\right)}{\partial \boldsymbol{x}_{k}}\right|_{\boldsymbol{x}_{\mathrm{op}, k}, \mathbf{0}} Gk=∂xk∂g(xk,nk)∣∣xop,k,0
- n k ′ = ∂ g ( x k , n k ) ∂ n k ∣ x o p , k , 0 n k \boldsymbol{n}_{k}^{\prime}=\left.\frac{\partial \boldsymbol{g}\left(\boldsymbol{x}_{k}, \boldsymbol{n}_{k}\right)}{\partial \boldsymbol{n}_{k}}\right|_{\boldsymbol{x}_{\mathrm{op}, k}, \mathbf{0}} \boldsymbol{n}_{k} nk′=∂nk∂g(xk,nk)∣∣xop,k,0nk
任意一个点 x o p , k \boldsymbol{x}_{\mathrm{op}, k} xop,k 进行线性化,可得:
需要注意的是,观测模型和雅可比矩阵均在 x o p , k \boldsymbol{x}_{\mathrm{op}, k} xop,k 处计算。(在EKF中, x o p , k = x ˇ k \boldsymbol{x}_{\mathrm{op}, k}=\check{\boldsymbol{x}}_{k} xop,k=xˇk)
使用上面的线性化模型,我们可以将时刻 k k k 处的状态和测量的联合概率近似为高斯分布,即:
p ( x k , y k ∣ x ˇ 0 , v 1 : k , y 0 : k − 1 ) ≈ N ( [ μ x , k μ y , k ] , [ Σ x x , k Σ x y , k Σ y x , k Σ y y , k ] ) = N ( [ x ˇ k y o p , k + G k ( x ˇ k − x o p , k ) ] , [ P ˇ k P ˇ k G k T G k P ˇ k G k P ˇ k G k T + R k ′ ] ) \begin{aligned}& p\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{k} \mid \check{\boldsymbol{x}}_{0}, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k-1}\right) \approx \mathcal{N}\left(\left[\begin{array}{c}\boldsymbol{\mu}_{x, k} \\\boldsymbol{\mu}_{y, k}\end{array}\right],\left[\begin{array}{cc}\boldsymbol{\Sigma}_{x x, k} & \boldsymbol{\Sigma}_{x y, k} \\\boldsymbol{\Sigma}_{y x, k} & \boldsymbol{\Sigma}_{y y, k}\end{array}\right]\right) \\=& \mathcal{N}\left(\left[\begin{array}{cc}\check{\boldsymbol{x}}_{k} \\\boldsymbol{y}_{\mathrm{op}, k}+\boldsymbol{G}_{k}\left(\check{\boldsymbol{x}}_{k}-\boldsymbol{x}_{\mathrm{op}, k}\right)\end{array}\right],\left[\begin{array}{cc}\check{\boldsymbol{P}}_{k} & \check{\boldsymbol{P}}_{k}\boldsymbol{G}_{k}^{\mathrm{T}} \\\boldsymbol{G}_{k} \check{\boldsymbol{P}}_{k} & \boldsymbol{G}_{k} \check{\boldsymbol{P}}_{k} \boldsymbol{G}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}^{\prime}\end{array}\right]\right)\end{aligned} =p(xk,yk∣xˇ0,v1:k,y0:k−1)≈N([μx,kμy,k],[Σxx,kΣyx,kΣxy,kΣyy,k])N([xˇkyop,k+Gk(xˇk−xop,k)],[PˇkGkPˇkPˇkGkTGkPˇkGkT+Rk′])
如果测量值 y k \boldsymbol{y}_{k} yk 已知,我们可以利用高斯推断得到 x k \boldsymbol{x}_{k} xk 的条件概率密度(即后验):
p ( x k ∣ x ˇ 0 , v 1 : k , y 0 : k ) = N ( μ x , k + Σ x y , k Σ y y , k − 1 ( y k − μ y , k ) ⏟ x ^ k , Σ x x , k − Σ x y , k Σ y y , k − 1 Σ y x , k ⏟ P ^ k ) \begin{aligned}& p\left(\boldsymbol{x}_{k} \mid \check{\boldsymbol{x}}_{0}, \boldsymbol{v}_{1: k}, \boldsymbol{y}_{0: k}\right) \\=& \mathcal{N}(\underbrace{\boldsymbol{\mu}_{x, k}+\boldsymbol{\Sigma}_{x y, k} \boldsymbol{\Sigma}_{y y, k}^{-1}\left(\boldsymbol{y}_{k}-\boldsymbol{\mu}_{y, k}\right)}_{\hat{\boldsymbol{x}}_{k}}, \underbrace{\boldsymbol{\Sigma}_{x x, k}-\boldsymbol{\Sigma}_{x y, k} \boldsymbol{\Sigma}_{y y, k}^{-1} \boldsymbol{\Sigma}_{y x, k}}_{\hat{\boldsymbol{P}}_{k}})\end{aligned} =p(xk∣xˇ0,v1:k,y0:k)N(x^kμx,k+Σxy,kΣyy,k−1(yk−μy,k),P^kΣxx,k−Σxy,kΣyy,k−1Σyx,k)
令 K k = Σ x y , k Σ y y , k − 1 = P ˇ k G k T ( G k P ˇ k G k T + R k ′ ) − 1 \boldsymbol{K}_{k}=\boldsymbol{\Sigma}_{x y,k} \boldsymbol{\Sigma}_{y y,k}^{-1}=\check{\boldsymbol{P}}_{k} \boldsymbol{G}_{k}^{\mathrm{T}}\left(\boldsymbol{G}_{k} \check{\boldsymbol{P}}_{k} \boldsymbol{G}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}^{\prime}\right)^{-1} Kk=Σxy,kΣyy,k−1=PˇkGkT(GkPˇkGkT+Rk′)−1(卡尔曼增益),则得到:
P ^ k = ( 1 − K k G k ) P ˇ k \hat{\boldsymbol{P}}_{k} =\left(\mathbf{1}-\boldsymbol{K}_{k} \boldsymbol{G}_{k}\right) \check{\boldsymbol{P}}_{k} P^k=(1−KkGk)Pˇk
x ^ k = x ˇ k + K k ( y k − y o p , k − G k ( x ˇ k − x o p , k ) ) \hat{\boldsymbol{x}}_{k} =\check{\boldsymbol{x}}_{k}+\boldsymbol{K}_{k}\left(\boldsymbol{y}_{k}-\boldsymbol{y}_{\mathrm{op}, k}-\boldsymbol{G}_{k}\left(\check{\boldsymbol{x}}_{k}-\boldsymbol{x}_{\mathrm{op}, k}\right)\right) x^k=xˇk+Kk(yk−yop,k−Gk(xˇk−xop,k))
可以看出,IEKF中的卡尔曼增益和更新方程与EKF非常相似,唯一的区别在于线性化的工作点。如果将线性化的工作点设置为预测先验的均值(即 x o p , k = x ˇ k \boldsymbol{x}_{\mathrm{op}, k}=\check{\boldsymbol{x}}_{k} xop,k=xˇk),那么IEKF就等价于EKF。
然而,如果我们迭代的重新计算 x ^ k \hat{\boldsymbol{x}}_{k} x^k , 并且在每一次迭代中将工作点设置为上一次迭代的后验均值(即令 x o p , k = x ^ k \boldsymbol{x}_{\mathrm{op}, k}=\hat{\boldsymbol{x}}_{k} xop,k=x^k ),将得到更好的结果。
在第一次迭代中, 我们令 x o p , k = x ˇ k \boldsymbol{x}_{\mathrm{op}, k}=\check{\boldsymbol{x}}_{k} xop,k=xˇk,这使得我们能够对更好的估计进行线性化, 从而改进每次迭代的近似程度。在迭代的过程中,若 x o p , k \boldsymbol{x}_{\mathrm{op}, k} xop,k 的改变足够小就终止迭代。
注意,卡尔曼增益方程和更新方程收敛之后,协方差方程只需要计算一次。
边栏推荐
猜你喜欢
随机推荐
搭建好pytorch环境后,pip和conda指令不能用
我的祖国
Jar a key generation document database
【LeetCode】最长公共子序列(动态规划)
Minimized installation of debian11
Apple told Qualcomm: I bought a new campus for $445 million and may plan to speed up self-development of baseband chips
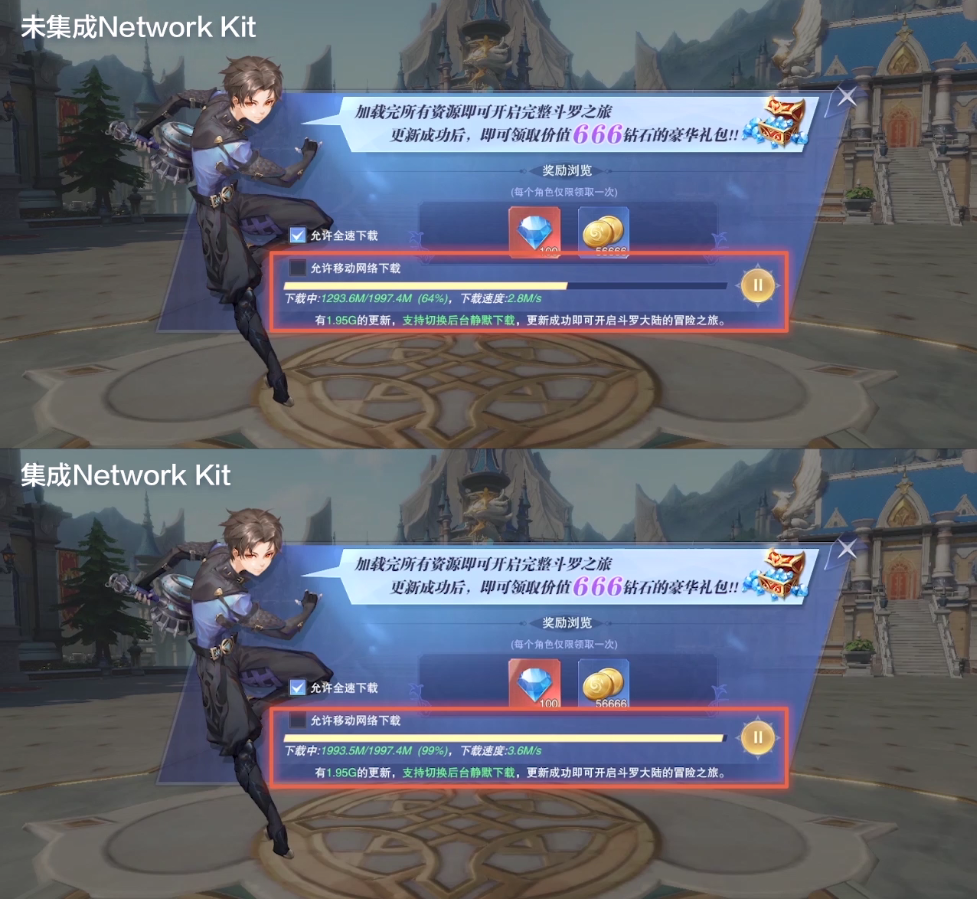
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
智能座舱的「交互设计」大战
免费的公共WiFi不要乱连,遭中间人攻击了吧?
Nanoprobes 棕榈酰纳米金相关说明书
Shell 用法梳理总结
一文搞定 SQL Server 执行计划
Prometheus监控Harbor(二进制版)
响应式织梦模板除尘器类网站
密码学基础以及完整加密通讯过程解析
米哈游--测试开发提前批
小身材有大作用——光模块基础知识(一)
做项目一定用得到的NLP资源【分类版】
BioVendor人Clara细胞蛋白(CC16)Elisa试剂盒检测步骤
The longest substring that cannot have repeating characters in a leetcode/substring