Teacher wangshuyao's notes on operations research 04 fundamentals of linear algebra

The first 4 speak Fundamentals of linear algebra

Linear algebra is through a series of means “ Toss about ” Equations , Extract the system information .

The purpose of linear algebra

Solve a system of linear equations （ The degree of the linear equation, that is, the unknown number, is 1 The equation of ）.

Steps of solving linear equations

1. Judge whether there is a solution
2. How to solve
3. How to express solutions

Some classical ideas of linear algebra and analytic geometry

For binary linear equations $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2=b_1\\ a_{21}{x}_1+a_{22}{x}_2=b_2\end{array}$, The two equations of this system represent two straight lines in space . If two lines intersect , The equations have solutions , And the solution of the equations is the intersection of two straight lines ; And if two straight lines are parallel , The equations have no solution , When the coefficients of two straight lines are proportional, they are parallel .

For ternary linear equations $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3=b_2\end{array}$, The two equations of the system of equations represent two planes in space . If two planes intersect , Then the line where two planes intersect is the solution of the equations , The equations have infinite solutions . If two planes are parallel , The equations have no solution , When the two plane coefficients are proportional, they are parallel .

For ternary linear equations $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3=b_2\\ a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3=b_3\end{array}$, The three equations of the system of equations represent three planes in space . Three planes can intersect at the same point , The same point is the unique solution of these three equations ; They can also intersect on the same line , This is the case of infinite solutions ; At least two planes can also coincide and intersect with the third plane （ Including the case that three planes coincide ）, This is also the case of infinite solutions ; Of course , At least one plane does not intersect with other planes （ For example, the three planes are parallel to each other , Or when two planes are recombined and parallel to the third plane ）, Or the intersection lines of the three planes neither coincide nor intersect at the same point , Then this is no solution .

Methodology of solving linear equations

Inspired by the solution of low dimensional linear equations , More generally , about $n$ A system of elementary linear equations $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+\cdots +a_{2n}{x}_n=b_2\\ \dots \\ a_{n1}{x}_1+a_{n2}{x}_2+a_{n3}{x}_3+\cdots +a_{nn}{x}_n=b_n\end{array}$, To solve a system of equations , The core idea is to extract the system information of these equations , Then use the elimination method to solve the equations . Using matrix and matrix multiplication in linear algebra , The system information of the equations can be well extracted .

matrix

How to treat matrix

For binary linear equations $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2=b_1\\ a_{21}{x}_1+a_{22}{x}_2=b_2\end{array}$, The coefficient matrix is $\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$, To judge whether the linear equations have solutions , Only one row vector of its coefficient matrix needs to be judged （ Or column vectors ） Whether it can be used by another row vector （ Or column vectors ） Linear representation .

about $n$ Meta linear equations are similar , To judge whether the linear equations have solutions , Only one row vector of its coefficient matrix needs to be judged （ Or column vectors ） Whether it can be used by the remaining row vectors （ Or column vectors ） Linear representation . Replace all vectors that can be linearly represented by the remaining vectors with 0, The number of vectors that cannot be linearly represented by the remaining vectors is the rank of the matrix , It represents the essential attribute of matrix . Then we can discuss the solution of linear equations according to the rank of the matrix , For details, please refer to the relevant knowledge in linear algebra .

The solution of matrix rank

You can do elementary row transformation on the matrix , Reduce it to a stepped matrix and find the rank of the matrix .

For shapes like $n\times m$ The rank of the matrix of $R\le min(n,m)$.

The basis of a matrix

According to the rank of the matrix $R$ Find one in the matrix $R$ Order is not 0 The determinant of （ At least one such determinant can be found ）, Arrange the elements in the determinant in order into a matrix , This matrix is a base of the original matrix .

The matrix of the inverse

Finding the inverse of a matrix

Find the inverse matrix with elementary row transformation . The matrix $(A,E)$ Perform elementary line transformation , Make it into a $(E,B)$, be $B$ Namely $A$ The inverse matrix $A^{-1}$.

Properties of matrix inverse

$A\cdot A^{-1}=E$

determinant

What are the ranks

Determinant is an algorithm , and $+、-$ similar , You can calculate a number . Of course, determinant can also be regarded as a number .

Geometric meaning of determinant

For determinants $\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|$, The corresponding matrix is $\left[\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right]$, Its row vector ${\alpha }_1=$$\left[\begin{array}{cc}{a}_1& a_2\end{array}\right]$,${\alpha }_2=$$\left[\begin{array}{cc}{b}_1& b_2\end{array}\right]$, Draw these two vectors in the figure below .

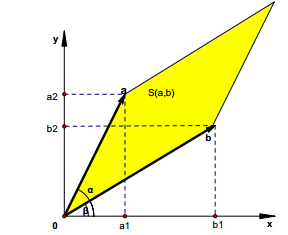
You can find the area of the Yellow parallelogram in the figure $S=-absin(\alpha -\beta )$, The meaning of each symbol is shown in the figure . In addition, the clockwise area is negative , Counterclockwise area is positive , This is a directed area , Because the picture is clockwise , So there is also a minus sign in front , Is the actual area . Then simplify it to $S=a_1{b}_2-a_2{b}_1$.

Sum up , The geometric meaning of second-order determinant is the area of parallelogram .

The geometric meaning of the third-order determinant is the volume of the parallelepiped .

$n$ The geometric meaning of order determinant is $n$ Volume of dimensional hypercube .

therefore , If the value of determinant is 0, Then the corresponding matrix has redundant （ Not independent ） Vector ; conversely , Then the corresponding matrix is full rank .

summary

The purpose of linear algebra is to solve linear equations , It can be cleverly combined with analytic geometry .

Information can be extracted from the coefficients of linear equations , Build it into a matrix , And the unknown number is also expressed as a matrix , We can use matrix multiplication to express linear equations .

Independent in the matrix （ Linearly independent ） The number of vectors is the rank of the matrix , It reflects the essential attribute of matrix .

According to the rank of the matrix $R$ Find one in the matrix $R$ Order is not 0 The determinant of , Arrange the elements in the determinant in order into a matrix , This matrix is a base of the original matrix .

Determinant is an algorithm , Its geometric meaning is the area of a parallelogram composed of two vectors （ Take the second-order determinant as an example ）.